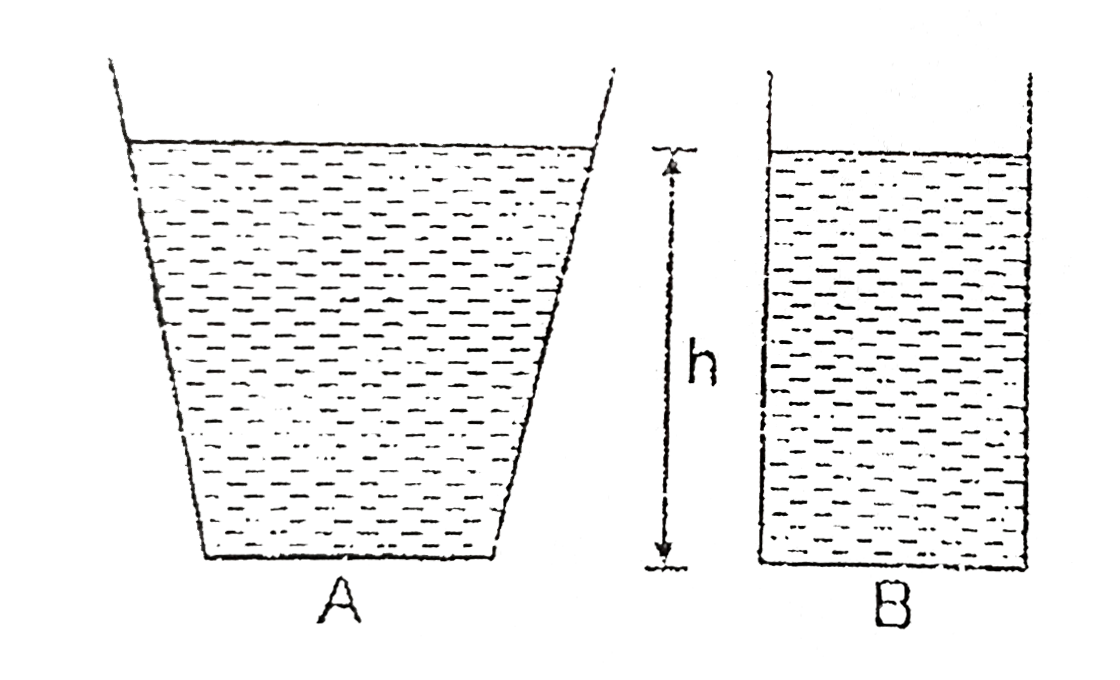
A vessel in the form of a truncated cone has base area a1 and top area a2. It is filled to the brim with a liquid. The force at the bottom of the vessel is
a.Equal to weight of the liquid, if a1<a2
b.Greater than weight of the liquid, if a2<a1
c.Less than weight of the liquid, if a1<a2
d.Equal to weight of the liquid, for any value of the areas
The correct Answer is:B, C
To find the force at the bottom of a truncated cone vessel filled with liquid, we can follow these steps:
Step 1: Understand the System
The vessel is in the form of a truncated cone with a base area A1 and a top area A2. It is filled with a liquid, and we need to analyze the forces acting at the bottom of the vessel.
Step 2: Identify the Weight of the Liquid
The weight of the liquid (W) can be expressed as:
W=ρVg
where ρ is the density of the liquid, V is the volume of the liquid, and g is the acceleration due to gravity.
Step 3: Calculate the Volume of the Liquid
The volume V of the liquid in a truncated cone can be calculated using the formula:
V=13h(A1+A2+√A1A2)
where h is the height of the liquid column.
Step 4: Determine the Force at the Bottom
The force F at the bottom of the vessel is the sum of the weight of the liquid and the normal force exerted by the liquid on the bottom surface. The normal force acts vertically upward and balances the weight of the liquid. Therefore, the total force at the bottom can be expressed as:
F=W+Nv
where Nv is the vertical component of the normal force.
Step 5: Analyze the Cases
1. Case 1: If A1<A2 (the base area is smaller than the top area), the force at the bottom will be equal to the weight of the liquid since the normal force will not contribute additional force.
2. Case 2: If A1>A2 (the base area is larger than the top area), the force at the bottom will be greater than the weight of the liquid due to the additional normal force acting downwards.
Step 6: Conclusion
From the analysis, we can conclude:
- If A1<A2, then F=W.
- If A1>A2, then F>W.
- If A1=A2, then F=W.
Thus, the force at the bottom of the vessel is equal to the weight of the liquid when A1<A2 and greater than the weight of the liquid when A1>A2.
Final Answer
The correct options based on the analysis are:
- Greater than the weight of the liquid if A1>A2.
- Equal to the weight of the liquid if A1<A2.
The vessel is in the form of a truncated cone with a base area A1 and a top area A2. It is filled with a liquid, and we need to analyze the forces acting at the bottom of the vessel.
The weight of the liquid (W) can be expressed as:
W=ρVg
where ρ is the density of the liquid, V is the volume of the liquid, and g is the acceleration due to gravity.
The volume V of the liquid in a truncated cone can be calculated using the formula:
V=13h(A1+A2+√A1A2)
where h is the height of the liquid column.
The force F at the bottom of the vessel is the sum of the weight of the liquid and the normal force exerted by the liquid on the bottom surface. The normal force acts vertically upward and balances the weight of the liquid. Therefore, the total force at the bottom can be expressed as:
F=W+Nv
where Nv is the vertical component of the normal force.
1. Case 1: If A1<A2 (the base area is smaller than the top area), the force at the bottom will be equal to the weight of the liquid since the normal force will not contribute additional force.
2. Case 2: If A1>A2 (the base area is larger than the top area), the force at the bottom will be greater than the weight of the liquid due to the additional normal force acting downwards.
From the analysis, we can conclude:
- If A1<A2, then F=W.
- If A1>A2, then F>W.
- If A1=A2, then F=W.
The correct options based on the analysis are:
- Greater than the weight of the liquid if A1>A2.
- Equal to the weight of the liquid if A1<A2.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:SECTION - D
Explore 2 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:SECTION - E
Explore 8 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:SECTION - B
Explore 23 Videos
- MAGNETISM AND MATTER Book:AAKASH INSTITUTE ENGLISHChapter:MAGNETISM AND MATTER Exercise:ASSIGNMENT (SECTION D)
Explore 26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Assignment(Section-D)
Explore 14 Videos
Similar Questions
Two vessels A and B of different shapes have the same base area and are filled with water up to the same height h (see figure). The force exerted by water on the base is FA for vessel A and FB for vessel B. The respective weights of the water filled in vessels are WA and WB. Then
View SolutionA vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
View SolutionA vessel in the form of inverted cone. Its height is 8 cm and radius of its top, which is open, is 5 cm. It is filled with water upto the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped in the vessel, one fourth of the water flows out. Find the number of lead shots dropped in the vessel.
View SolutionA vessel of base area 100cm×60cm and height 200cm is completely filled with a liquid of density 1.1×103kgm−3.
(a) Ignoring the atmospheric pressure, find :
(i) the thrust at the bottom of the vessel,
(ii) the pressure at the bottom of the vessel,
(iii) The pressure at a depth of 5 cm from the free surface,
(iv) the net force experienced by a metal foil of area 10cm2 placed at a depth of 5 cm from the free surface,
(b) The thrust at the bottom of the vessel if the atmospheric pressure equal to 1×105Nm−2 is taken into account.
Take g=9.8ms−2 .
View SolutionA tube 1cm2 in cross- section is attached to the top of a vessel 1 cm high and of cross - section 100 cm2 Water is poured into the system filling it to a depth of 100 cm above the bottom of the vessel as shown in fig. Take g =10 ms−2 .

View SolutionA tube 1cm2 in cross- section is attached to the top of a vessel 1 cm high and of cross - section 100 cm2 Water is poured into the system filling it to a depth of 100 cm above the bottom of the vessel as shown in fig. Take g =10 ms−2 .

View SolutionTwo identical cylindrical vessels have the same base area but are filled with different volumes of water . The forces on the bases of the two vessels are same ?
View SolutionA cylindrical vessel of area of cross section A is filled with a liquid up to a height H. A very small hole of area of cross section a is made at the bottom of the vellel. Find the time taken by the vessel to become empty.
View SolutionA vessel, in the form of an inverted cone, is filled with water to the brim. Its height is 32 cm and diameter of the base is 25.2 cm. Six equal solid cones are dropped in it, so that they are fully submerged. As a result, one-fourth of water in the original cone overflows. What is the volume of each of the solid cones submerged ?
View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View Solution