Let f(x)=ax2+bx+c,a≠0, such the f(−1−x)=f(−1+x)∀x∈R. Also given that f(x)=0 has no real roots and 4a+b>0.
Let α=4a−2b+c,β=9a+3b+c,γ=9a−3b+c, then which of the following is correct ?
β<α<γ
γ<α<β
α<γ<β
α<β<γ
The correct Answer is:C
To solve the problem, we start with the function given:
f(x)=ax2+bx+c
where a≠0. We are given that:
f(−1−x)=f(−1+x)∀x∈R
Step 1: Analyzing the Symmetry Condition
The condition f(−1−x)=f(−1+x) implies that the function is symmetric about x=−1. This means that the vertex of the parabola represented by f(x) lies on the line x=−1.
Step 2: Finding the Vertex
The vertex xv of a quadratic function f(x)=ax2+bx+c is given by:
xv=−b2a
Setting this equal to -1 for symmetry, we have:
−b2a=−1⟹b=2a
Step 3: Substituting b into the Function
Now substituting b=2a into the function:
f(x)=ax2+2ax+c
Step 4: Condition for No Real Roots
The condition that f(x)=0 has no real roots implies that the discriminant must be negative:
D=b2−4ac<0
Substituting b=2a:
(2a)2−4ac<0⟹4a2−4ac<0⟹a2−ac<0⟹a(a−c)<0
This means either a>0 and c<a or a<0 and c>a. Given 4a+b>0:
4a+2a>0⟹6a>0⟹a>0
Thus, we conclude a>0 and c<a.
Step 5: Calculating α,β,γ
Now we calculate α,β,γ:
1. For α:
α=4a−2b+c=4a−2(2a)+c=4a−4a+c=c
2. For β:
β=9a+3b+c=9a+3(2a)+c=9a+6a+c=15a+c
3. For γ:
γ=9a−3b+c=9a−3(2a)+c=9a−6a+c=3a+c
Step 6: Comparing α,β,γ
Now we compare α,β,γ:
- We know α=c
- γ=3a+c
- β=15a+c
Since a>0, we have:
\alpha < \gamma < \beta \quad \text{(because c < a )}
Conclusion
Thus, the correct order is:
α<γ<β
The correct option is (C) α<γ<β.
α=4a−2b+c=4a−2(2a)+c=4a−4a+c=c
β=9a+3b+c=9a+3(2a)+c=9a+6a+c=15a+c
γ=9a−3b+c=9a−3(2a)+c=9a−6a+c=3a+c
- γ=3a+c
- β=15a+c
\alpha < \gamma < \beta \quad \text{(because c < a )}
Topper's Solved these Questions
- QUADRATIC EQUATIONS Book:VK JAISWAL ENGLISHChapter:QUADRATIC EQUATIONS Exercise:EXERCISE (MATCHING TYPE PROBLEMS)
Explore 3 Videos
- QUADRATIC EQUATIONS Book:VK JAISWAL ENGLISHChapter:QUADRATIC EQUATIONS Exercise:EXERCISE (SUBJECTIVE TYPE PROBLEMS)
Explore 43 Videos
- QUADRATIC EQUATIONS Book:VK JAISWAL ENGLISHChapter:QUADRATIC EQUATIONS Exercise:EXERCISE (ONE OR MORE THAN ONE ANSWER IS/ARE CORRECT)
Explore 42 Videos
- PROBABILITY Book:VK JAISWAL ENGLISHChapter:PROBABILITY Exercise:Exercise -5 : Subjective Type problems
Explore 11 Videos
- SEQUENCE AND SERIES Book:VK JAISWAL ENGLISHChapter:SEQUENCE AND SERIES Exercise:EXERCISE (SUBJECTIVE TYPE PROBLEMS)
Explore 21 Videos
Similar Questions
Knowledge Check
If f(x)=ax2+bx+c,a≠0 and a, b , and c are all negative , which could be the graph of f(x) ?
A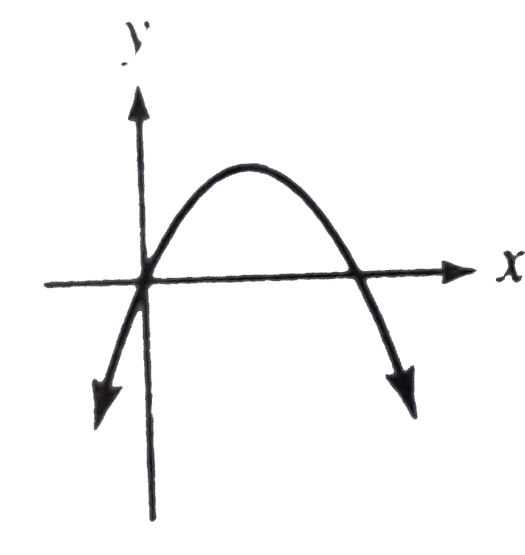 B
B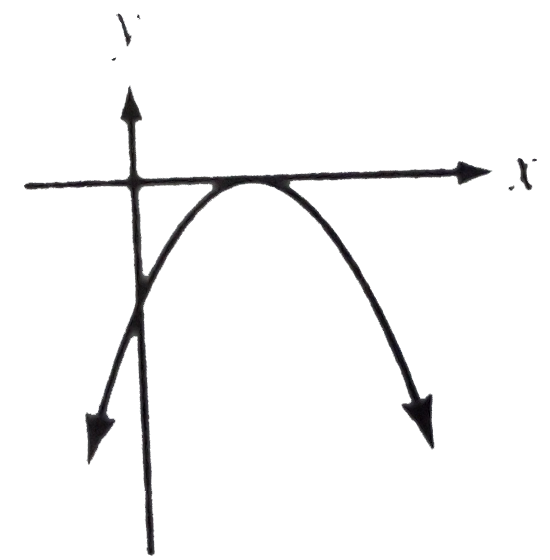 C
C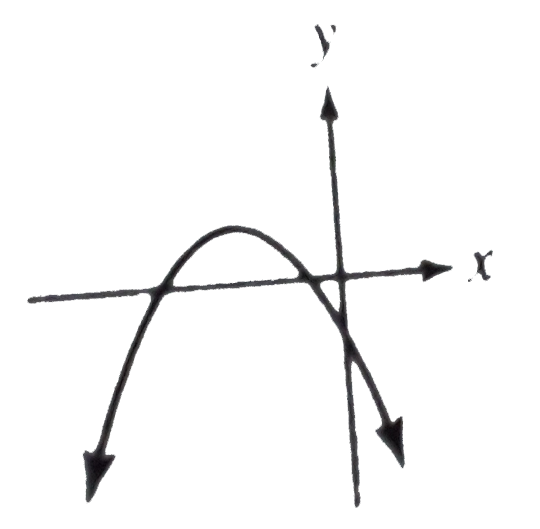 D
D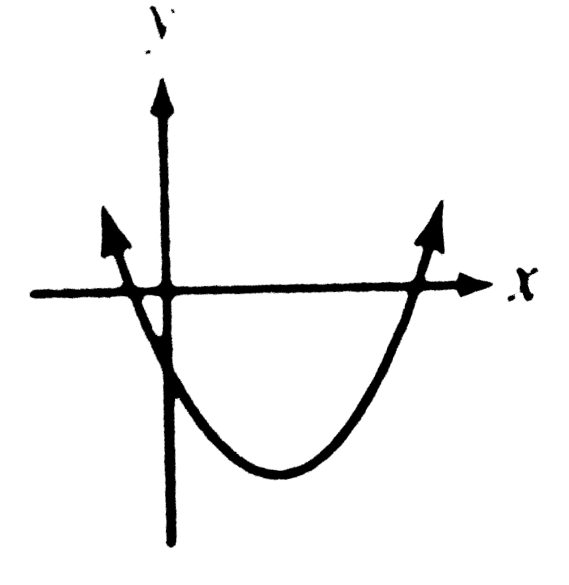
Let f(x)=ax2−bx+c2,b≠0andf(x)≠0 for all x∈R. Then
View SolutionIf f(x)=ax2+bx+c , where a≠0,b,c∈ R , then which of
the following conditions implies that f(x) has real roots?
View SolutionLet f(x) =ax3+bx2+cx+d,a≠0, where a, b, c, d∈R. If f(x) is one-one and onto, then which of the following is correct ?
View SolutionLet f(x)=ax2+bx+c and f(−1)<1,f(1)>−1,f(3)<−4 and a≠0, then
View SolutionIf f(x)=ax2+bx+c satisfies the identity f(x+1)−f(x)=8x+3 for all x∈R Then (a,b)=
View SolutionLet f(x)=ax2+bx+c, where a,b,c∈R,a≠0. Suppose |f(x)|≤1,x∈[0,1], then
View SolutionLet f(x)=ax2+bx+c,a,b,c,∈R and equation f(x)−x=0 has imaginary roots α,β. If r, s be the roots of f(f(x))−x=0, then ∣∣ ∣ ∣∣2αδβ0αγβ1∣∣ ∣ ∣∣ is
View Solution
