The first four terms of a sequence are given by T1=0,T2=1,T3=1,T4=2.The≥≠raltermsisgivenbyT_(n)=Aalpha ^(n -1) +B beta ^(n-1)whereA,B alpha, betaare∈dependentofaandAispositive.<br>Thevalueof5 (A^(2) + B ^(2) is equal to :
2
4
6
8
The correct Answer is:A
Step by step video & image solution for The first four terms of a sequence are given by T_(1)=0, T_(2)=1, T_(3) =1, T_(4) =2. The general terms is given by T_(n)=Aalpha ^(n -1) +B beta ^(n-1) where A,B alpha, beta are independent of a and A is positive. The value of 5 (A^(2) + B ^(2) is equal to : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SEQUENCE AND SERIES BOOK - VK JAISWAL ENGLISHCHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE (MATCHING TYPE PROBLEMS)
4 Videos
- SEQUENCE AND SERIES BOOK - VK JAISWAL ENGLISHCHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
21 Videos
- SEQUENCE AND SERIES BOOK - VK JAISWAL ENGLISHCHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE (ONE OR MORE THAN ONE ANSWER IS/ARE CORRECT)
19 Videos
- QUADRATIC EQUATIONS BOOK - VK JAISWAL ENGLISHCHAPTER - QUADRATIC EQUATIONS EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
43 Videos
- SOLUTION OF TRIANGLESBOOK - VK JAISWAL ENGLISHCHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-5 : Subjective Type Problems
9 Videos
Similar Questions
What is the 20thterm of the sequence defined by an=(n−1)(2−n)(3+n)?
View SolutionFind the first five terms of the sequence for which t1=1,t2=2andtn+2=tn+tn+1
View SolutionWrite the first five terms of the sequence whose nthterms are : an=nn+1
View SolutionThe first two terms of a sequence are 0 and 1, The nth terms Tn=2Tn−1−Tn−2,n≥3. For example the third terms T3=2T2−T1=2−0=2, The sum of the first 2006 terms of this sequence is :
View SolutionGiven that T1=100N then find T2
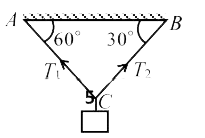
View SolutionFind the sum of the first 16 terms of a sequence whose nth term is given by tn=5n−3, where n is a nautral number.
View SolutionWrite the first five terms of the sequence whose nthterms are : an=(−1)n−15n+1
View SolutionIf A−B=π/4 , then (1+tanA)(1−tanB) is equal to 2 b. 1 c. 0 d. 3
View SolutionIf nth term (Tn) of the sequece is given by the relation Tn+1=Tn+2n,(nεN) and T1=3, then the value of ∞∑r=11Tr−1 equals
View SolutionThe first term of a geometric sequence is 64, and the common ratio is 14.
For what value of n is tn=14?
View Solution
