In a ΔABC, if (II1)2+(I2I3)2=λR2, where I denotes incentre, I1,I2andI3 denote centres of the circles escribed to the sides BC, CA and AB respectively and R be the radius of the circum circle of ΔABC. Find λ.
The correct Answer is:16
To solve the problem, we need to find the value of λ in the equation:
(II1)2+(I2I3)2=λR2
where I is the incenter, I1,I2,I3 are the excenters opposite to sides BC,CA,AB respectively, and R is the circumradius of triangle ABC.
Step 1: Understand the Distances
We start by using the known formulas for the distances between the incenter and excenters:
1. The distance from the incenter I to the excenter I1 (opposite side BC):
II1=c⋅secA21
2. The distance between the excenters I2 and I3:
I2I3=a⋅cscA21
Step 2: Substitute the Distances
Now we can express II1 and I2I3 in terms of the sides of the triangle:
- For II1:
II1=c⋅secA2
- For I2I3:
I2I3=a⋅cscA2
Step 3: Square the Distances
Next, we square both distances:
1. (II1)2:
(II1)2=(c⋅secA2)2=c2⋅sec2A2
2. (I2I3)2:
(I2I3)2=(a⋅cscA2)2=a2⋅csc2A2
Step 4: Combine the Squares
Now we combine these squared distances:
(II1)2+(I2I3)2=c2sec2A2+a2csc2A2
Step 5: Use Trigonometric Identities
We can use the identity sec2x=1+tan2x and csc2x=1+cot2x to simplify further, but we will directly substitute the values using the sine rule.
Step 6: Apply the Sine Rule
Using the sine rule, we know:
asinA=bsinB=csinC=2R
Thus, we can express a and c in terms of R:
- a=2RsinA
- c=2RsinC
Step 7: Substitute Back
Now substitute a and c back into the equation:
(2RsinC)2sec2A2+(2RsinA)2csc2A2
Step 8: Factor Out R2
Factoring out 4R2:
4R2(sin2Csec2A2+sin2Acsc2A2)
Step 9: Simplify Using Trigonometric Identities
Using sec2A2=1+tan2A2 and csc2A2=1+cot2A2, we can simplify further. However, we can also directly use the identity sin2x+cos2x=1.
Step 10: Final Equation
Finally, we have:
4R2=λR2
Dividing both sides by R2 (assuming R≠0) gives:
λ=4
Conclusion
Thus, the value of λ is:
4
II1=c⋅secA21
I2I3=a⋅cscA21
II1=c⋅secA2
I2I3=a⋅cscA2
(II1)2=(c⋅secA2)2=c2⋅sec2A2
(I2I3)2=(a⋅cscA2)2=a2⋅csc2A2
- c=2RsinC
Topper's Solved these Questions
- INVERSE TRIGONOMETRIC FUNTIONS Book:VK JAISWAL ENGLISHChapter:INVERSE TRIGONOMETRIC FUNTIONS Exercise:Exercise-4 : Matching Type Problems
Explore 3 Videos
- INDEFINITE AND DEFINITE INTEGRATIONBook:VK JAISWAL ENGLISHChapter:INDEFINITE AND DEFINITE INTEGRATIONExercise:EXERCISE (SUBJECTIVE TYPE PROBLEMS)
Explore 29 Videos
- LIMITBook:VK JAISWAL ENGLISHChapter:LIMITExercise:EXERCISE (SUBJECTIVE TYPE PROBLEMS)
Explore 7 Videos
Similar Questions
Find the current I1, I2, & I3, in the circuit.
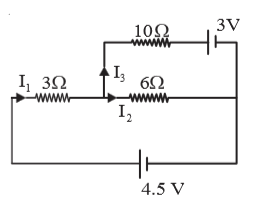
View SolutionIf I1 is the centre of the escribed circle touching side BC of !ABC in which ∠A=60∘, then I1 A =
View SolutionIf I is the incentre and I1,I2,I3 are the centre of escribed circles of the △ABC. Prove that
II1.II2.II3=16R2r.
View SolutionIf I1,I2,I3 are the centers of escribed circles of ΔABC, show that the area of ΔI1I2I3 is (abc)/(2r)
View SolutionLet ABC be a triangle with incentre I and inradius r. Let D, E, F be the feet of the perpendiculars from I to the sides BC, CA and AB, respectively, If r2 and r3 are the radii of circles inscribed in the quadrilaterls AFIE, BDIF and CEID respectively, then prove that r1r−r1+r2r−r2+r3r−r3=r1r2r3(r−r1)(r−r2)(r−r3)
View SolutionIf 1 is the incentre and 11,12,13 are the centre of escribed circles of the △ABC. Prove that
II1,II2,III3=16R2r.
View SolutionLet ABC be a triangle with incenter I and inradius r. Let D,E,andF be the feet of the perpendiculars from I to the sides BC,CA,andAB, respectively. If r1,r2andr3 are the radii of circles inscribed in the quadrilaterals AFIE,BDIF,andCEID, respectively, prove that r1r−11+r2r−r2+r3r−r3=r1r2r3(r−r1)(r−r2)(r−r3)
View SolutionIf I is the incenter of ΔABCandR1,R2,andR3 are, respectively, the radii of the circumcircle of the triangle IBC, ICA, and IAB, then prove that R1R2R3=2rR2
View SolutionIf I1,I2,I3 are excentres of the triangle with vertices (0, 0), (5, 12), (16, 12) then the orthocentre of ΔI1I2I3 is
View SolutionIn the given circuit, if I1andI2 be the current in resistances R1andR2, respectively, then
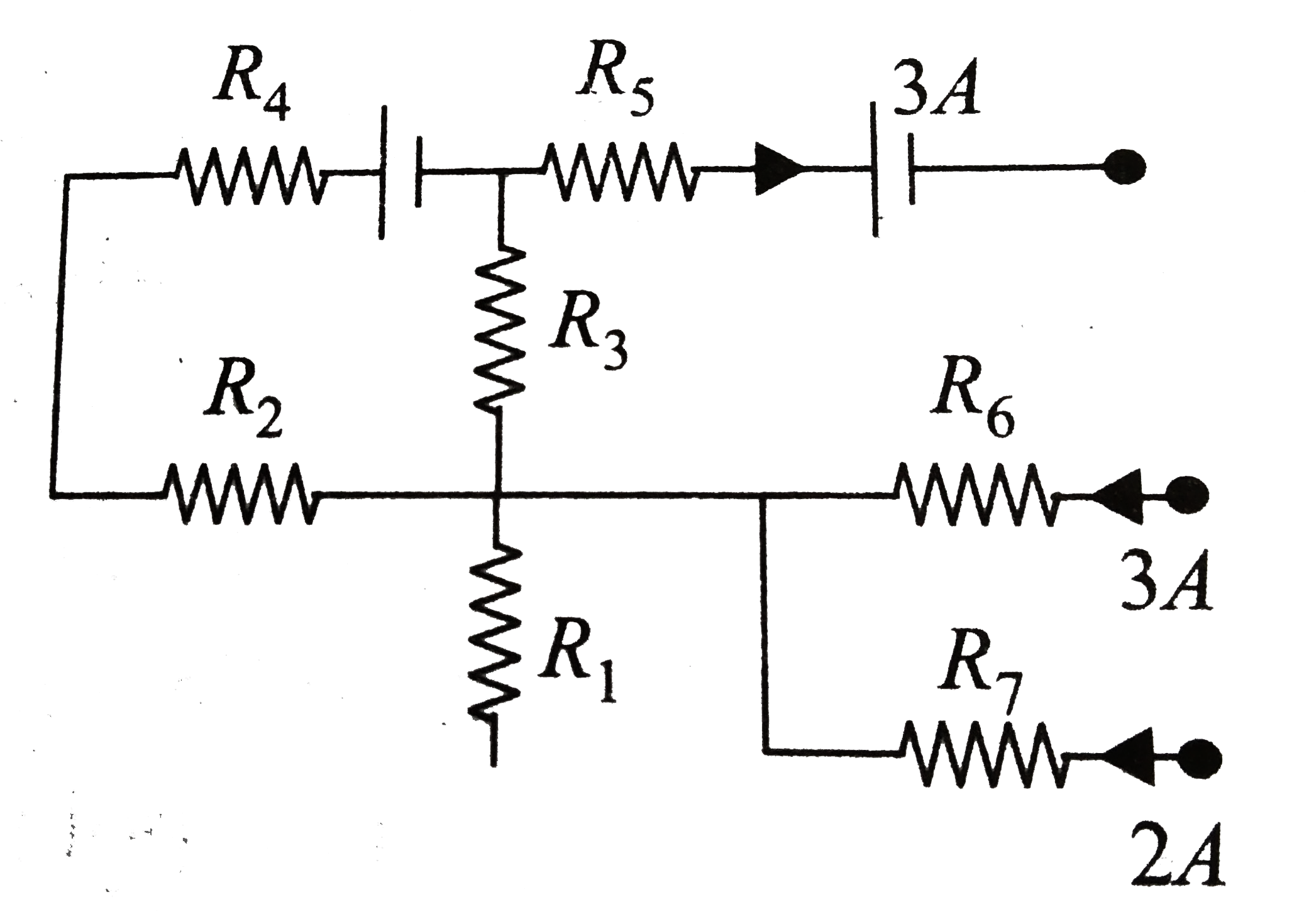 .
.
View Solution
