To determine the young's modulus of a wire , the formula is Y=FA.LΔl , where L = l ength ,A = area of cross - section of the wire , ΔL = change in the length of the wire when streched with a force F. Find the conversion factor to change it from CGS t o MKS system.
We know that the dimension of young's modulus is [ML−1T2] , i.e., a=1,b=−1,c=−2
CGSunit:gcm−1s−2andMKSunit:kgm−1s−2
By using the conversion formula:
∣∣
∣
∣
∣∣MKS systemCGS systemM1=1kgM2=1gL1=1mL2=1cmT1=1sT2=1s∣∣
∣
∣
∣∣
n2=n1[M1M2]1[[L1L−1]b[T1T2]−2=[gkg]1[cmm]−1[ss]−2
∴ Conversion factor =n2n1=[g103g]1[cm102cm]−1[ss]−2=110=0.1
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Exercise 1.116videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Exercise 1.26videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE1videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE1videos
FLUID MECHANICS
Similar Questions
A wire of length L,area of cross section A is hanging from a fixed support. The length of the wire changes to L1 when mass M is suspended from its free end. The expression for Young's modulus is:
View SolutionA load w is suspended from a wire of length l and area of cross-section A. Change in length of the wire is say Δl. Change in length Δl can be increased to two times by increasing
View Solution
Knowledge Check
- Question 1 - Select One
The young's modulus of a wire of length (L) and radius (r ) is Y. If the length is reduced toL2 and radius r2 , then its young's modulus will be
AY2BYC2YD4Y
A wire of natural length l, young's modulus Y and area of cross-section A is extended by x. Then, the energy stored in the wire is given by
View SolutionA wire of cross-sectional area A breaks due to its own weight when length of the wire is l. If area of cross-section of the wire is made 3A then maximum length of the wire can be hung without breaking is
View SolutionA force F doubles the length of wire of cross-section a The Young modulus of wire is
View SolutionA wire fixed at the upper end stretches by length l by applying a force F. The work done in stretching is
View SolutionI−V characterstic of a copper wire of length L and area fo cross-section A is shown in Fig. The slope of the curve becomes
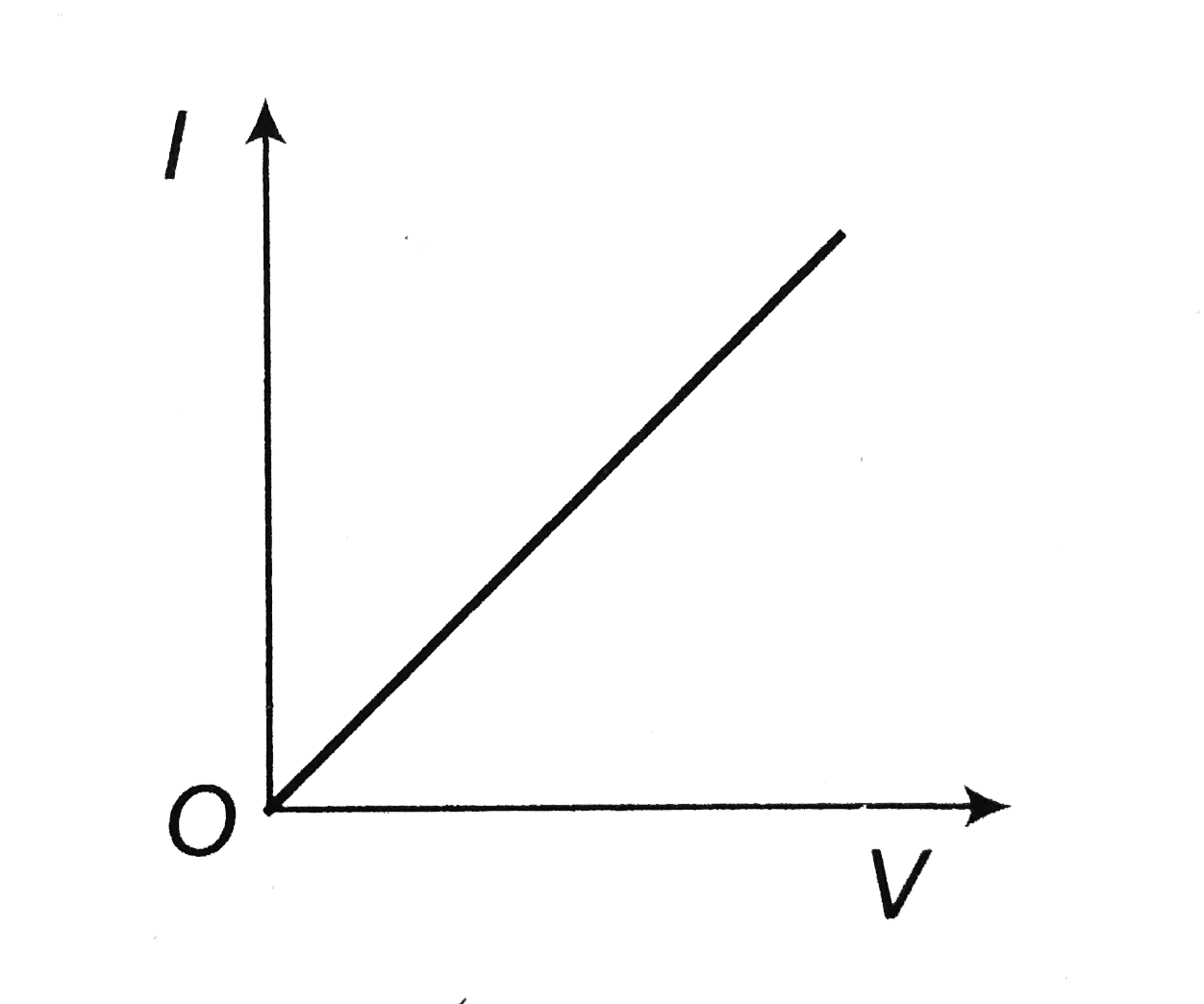 View Solution
View SolutionThe length of an iron wire is L and area of cross-section is A. The increase in length is l on applying the force F on its two ends. Which of the statement is correct
View SolutionThe young's modulus of a wire of length (L) and radius (r ) is Y. If the length is reduced toL2 and radius r2 , then its young's modulus will be
View Solution

