The resultant of two vectors $\to A$ and $\to B$ is perpendicular to the vector $\to A$ and its magnitudes is equal to half of the magnitudes of vector $\to B$ (figure). The angle between $\to A$ and $\to B$ is

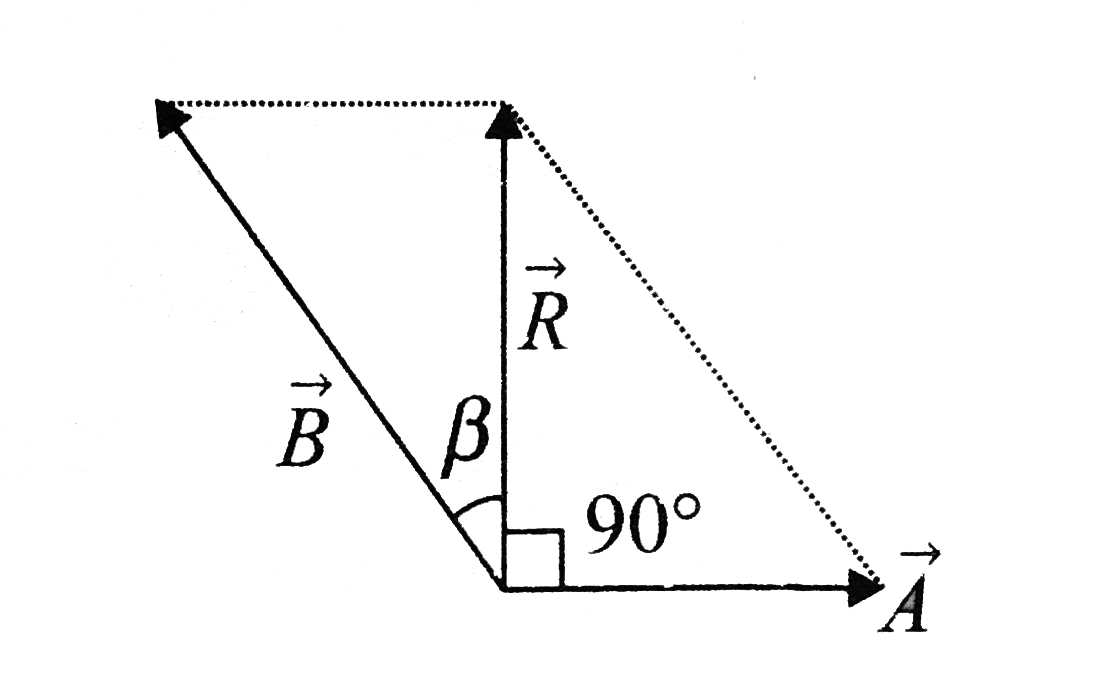
a. $120^{\circ}$

b. $150^{\circ}$

c. $135^{\circ}$

d. None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$cos β = \frac{R}{B} = \frac{1}{2} \Rightarrow β = 60^{\circ}$
Angle between $\to A$ and $\to B = 90^{\circ} + β = 150^{\circ}$

Updated on:21/07/2023

Class 11 PHYSICS VECTOR

Topper's Solved these Questions

VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Subjective
28 Videos
TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)
4 Videos

Knowledge Check

The magnitude of the x-component of vector $\to A$ is 3 and the magnitude of vector $\to A$ is 5. What is the magnitude of the y-component of vector $\to A$ ?
A3
B4
C5
D8

The resultant of two vectors $\to P$ and $\to Q$ is $\to R$ . If $\to Q$ is doubled then the new resultant vector is perpendicular to $\to P$ . Then magnitude of $\to R$ is :-
View Solution
a, b are the magnitudes of vectors $\to a$ & $\to b$ . If $\to a \times \to b = 0$ the value of $\to a . \to b$ is
View Solution
Two vectors $\to A and \to B$ lie in plane, another vector $\to C$ lies outside this plane, then the resultant of these three vectors i.e., $\to A + \to B + \to C$
View Solution
The resultant and dot product of two vectors $\to a and \to b$ is equal to the magnitude of $\to a$ . Show that when the vector $\to a$ is doubled , the new resultant is perpendicular to $\to b$ .
View Solution
The magnitudes of vectors $\to A, \to B and \to C$ are 3,4 and 5 unit respectively. If $\to A + \to B = \to C,$ the angle between $\to A and \to B$ is
View Solution
The vector $(\to a + 3 \to b)$ is perpendicular to $(7 \to a - 5 \to b)$ and $(\to a - 4 \to b)$ is perpendicular to $(7 \to a - 2 \to b)$ . The angle between $\to a$ and $\to b$ is :
View Solution
The magnitude of vector $\to A, \to B$ and $\to C$ are respectively 12,5 and 13 unit and $\to A + \to B = \to C$ then the angle between $\to A$ and $\to B$ is
View Solution

CENGAGE PHYSICS ENGLISH-VECTORS-Exercise Single Correct

From figure the correct relation is
04:05
Out of the following set of forces, the rsultant of which cannot be ze...
01:21
The resultant of two vectors vec(A) and vec(B) is perpendicular to the...
02:17
The ratio of maximum and minimum magnitudes of the resultant of two ve...
02:03
Two forces, each equal to F, act as shown in (figure) Their resultant ...
01:05
Vector vec(A) is 2cm long and is 60^(@) above the x-axis in the first ...
05:15
What is the angle between two vector forces of equal magnitude such th...
01:56
The angle between vec(A)+vec(B) and vec(A)xxvec(B) is
02:00
The projection of a vector vec(r )=3hat(i)+hat(j)+2hat(k) on the x-y p...
01:48
If |vec(A)+vec(B)|=|vec(A)|=|vec(B)| then the angle between vec(A) and...
01:33
If vectors A=hati+2hatj+4hatk and B=5hati represent the two sides of a...
03:53
Given |vec(A)(1)|=2,|vec(A)(2)|=3 and |vec(A)(1)+vec(A)(2)|=3. Find th...
03:09
Three vector vec(A),vec(B), vec(C ) satisfy the relation vec(A)*vec(B)...
02:24
If vec(A)=vec(B)+vec(C ), and the magnitudes of vec(A),vec(B),vec(C ) ...
01:34
Let A=hatiA cos theta+hatj A sin theta be any vector .Another vector B...
02:24
The angle which the vector vec(A)=2hat(i)+3hat(j) makes with the y-axi...
02:10
Given vec(P)=3hat(i)-4hat(j). Which of the following is perpendicular ...
01:11
In going from one city to another, a car travels 75km north, 60km nort...
03:30
What is the angle between vec(A) and vec(B), If vec(A) and vec(B) are ...
01:15
Two vectors vec(a) and vec(b) are such that |vec(a)+vec(b)|=|vec(a)-ve...
02:11

Home
Ask Doubt
Profile

The resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is

The correct Answer is:B

cosβ=RB=12⇒β=60∘ Angle between →A and →B=90∘+β=150∘

Topper's Solved these Questions

Similar Questions

Knowledge Check

The magnitude of the x-component of vector →A is 3 and the magnitude of vector →A is 5. What is the magnitude of the y-component of vector →A ?

CENGAGE PHYSICS ENGLISH-VECTORS-Exercise Single Correct

The resultant of two vectors $\to A$ and $\to B$ is perpendicular to the vector $\to A$ and its magnitudes is equal to half of the magnitudes of vector $\to B$ (figure). The angle between $\to A$ and $\to B$ is

$cos β = \frac{R}{B} = \frac{1}{2} \Rightarrow β = 60^{\circ}$
Angle between $\to A$ and $\to B = 90^{\circ} + β = 150^{\circ}$

The magnitude of the x-component of vector $\to A$ is 3 and the magnitude of vector $\to A$ is 5. What is the magnitude of the y-component of vector $\to A$ ?