Two cars 1 and 2 move with velocities v1 and v2, respectively, on a straight road in same direction When the cars are separated by a distance d the driver of car 1 applies brakes and the car moves with uniform retardation a1, Simultaneously, car 2 starts accelerating with a2, If v1<v2, find the minimum initial separation between the cars to avoid collision between then.
To solve the problem step by step, we will analyze the motion of both cars and derive the formula for the minimum initial separation d to avoid a collision.
Step 1: Understand the motion of both cars
- Car 1 is moving with an initial velocity v1 and applies brakes with a uniform retardation a1.
- Car 2 is moving with an initial velocity v2 and starts accelerating with an acceleration a2.
- We know that v1<v2.
Step 2: Define the final velocities
- Let v′1 be the final velocity of car 1 after applying brakes.
- Let v′2 be the final velocity of car 2 after accelerating.
Step 3: Use the kinematic equation
We will use the kinematic equation:
v2=u2+2as
For relative motion, we can express the relative velocities and accelerations.
Step 4: Set up the relative motion equation
The relative final velocity vrelative is:
vrelative=v′1−v′2
The initial relative velocity urelative is:
urelative=v1−v2
The relative acceleration arelative is:
arelative=−a1+a2
Step 5: Define the relative distance
The relative distance srelative is:
srelative=−d
Step 6: Substitute into the kinematic equation
Substituting these into the kinematic equation gives:
(v′1−v′2)2=(v1−v2)2+2(−a1+a2)(−d)
This simplifies to:
(v′1−v′2)2=(v1−v2)2+2(a2−a1)d
Step 7: Rearranging for d
Rearranging the equation to solve for d gives:
d=(v1−v2)2−(v′1−v′2)22(a2−a1)
Step 8: Conclusion
This equation provides the minimum initial separation d required to avoid a collision between the two cars.
- Car 1 is moving with an initial velocity v1 and applies brakes with a uniform retardation a1.
- Car 2 is moving with an initial velocity v2 and starts accelerating with an acceleration a2.
- We know that v1<v2.
- Let v′1 be the final velocity of car 1 after applying brakes.
- Let v′2 be the final velocity of car 2 after accelerating.
We will use the kinematic equation:
v2=u2+2as
For relative motion, we can express the relative velocities and accelerations.
The relative final velocity vrelative is:
vrelative=v′1−v′2
The initial relative velocity urelative is:
urelative=v1−v2
The relative acceleration arelative is:
arelative=−a1+a2
The relative distance srelative is:
srelative=−d
Substituting these into the kinematic equation gives:
(v′1−v′2)2=(v1−v2)2+2(−a1+a2)(−d)
This simplifies to:
(v′1−v′2)2=(v1−v2)2+2(a2−a1)d
Rearranging the equation to solve for d gives:
d=(v1−v2)2−(v′1−v′2)22(a2−a1)
This equation provides the minimum initial separation d required to avoid a collision between the two cars.
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Solved Examples
9 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.1
17 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
Two cars of same mass are moving with velocities v1andv2 respectively. If they are stopped by supplying same breaking power in time t1andt2 respectively then v1v2 is
View SolutionTwo cars A and B are moving in same direction with velocities 30 m/s and 20 m/s. When car A is at a distance d behind the car B, the driver of the car A applies brakes producing uniform retardation of 2m/s2. There will be no collision when :-
View Solution
Knowledge Check
A car starts from rest moves with uniform acceleration a1 for t1 second and then retards uniformly at a rate a2 for t2 second. Then t1/t2 is equal to
Aa1/a2Ba2/a1Ca22/a1D2a1/a2
A car moving with speed v on a straight road can be stopped with in distance d on applying brakes. If same car is moving with speed 3v and brakes provide half retardation, then car will stop after travelling distance
View SolutionA bird flies to and fro between two cars wich move with velocities v1 and v2, If the speed of the bird is v3 and the initial distance ofseparation between then is d, find the total distance covered bythe bird till the cars meet.
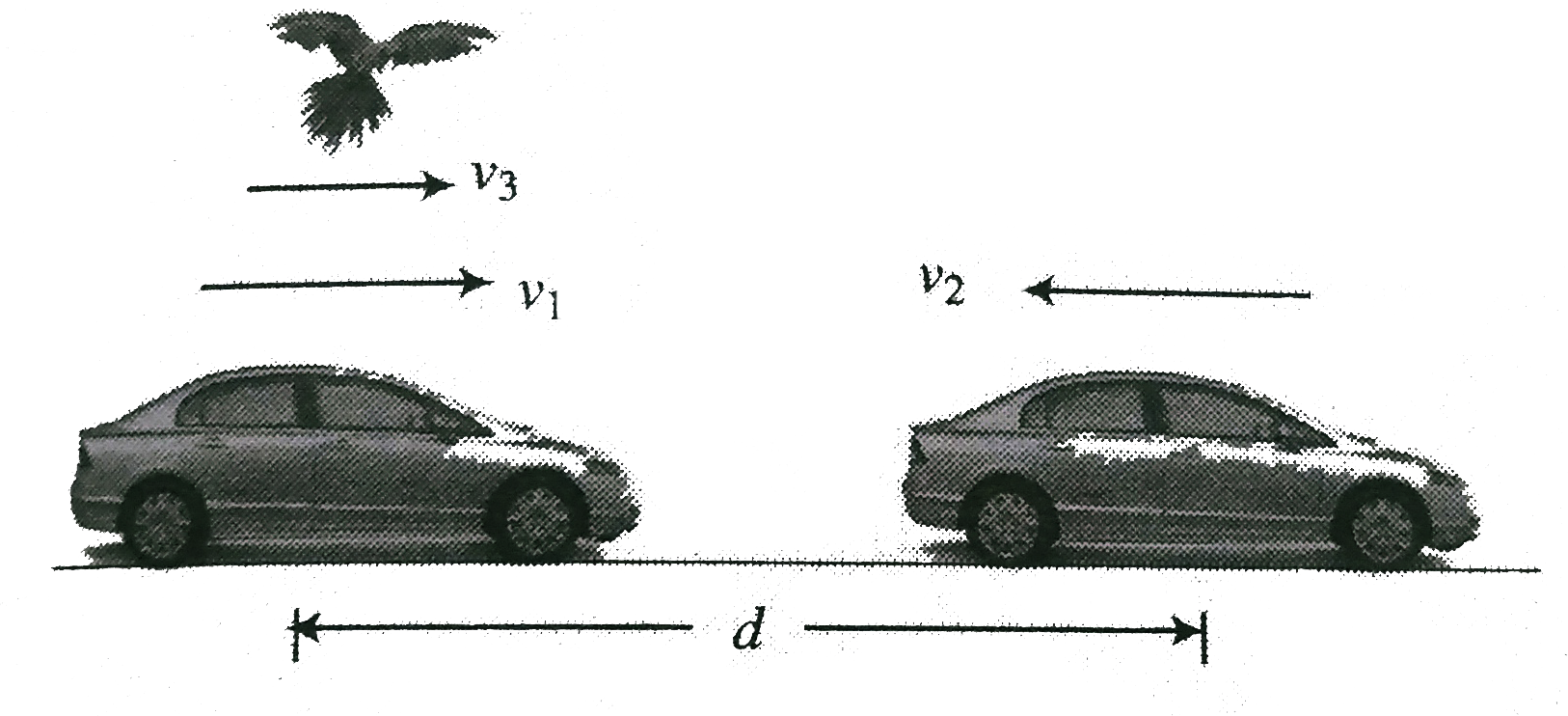 .
.
View SolutionA car is moving in a circular path with a uniform speed v. Find the magnitude of change in its velocity when the car rotates through an angle θ.
View SolutionTwo cars A and B are moving on the straight parallel paths with speeds 36kmh−1 and 72kmh−1 respectively starting from the same point in the same direction. After 20min, how much behind is car A and from car B?
View SolutionA car of mass m is driven with acceleration a along a straight level road against a constant external resistive force R. When the velocity of the car V, the rate at which the engine of the car is doing work will be
View SolutionA car of mass m is driven with acceleration a along a straight level road against a constant external resistive force R. When the velocity of the car V, the rate at which the engine of the car is doing work will be
View SolutionA car covers a distance of 89.1 km in 2.2 hours. What is the average distance covered by the car in 1 hour?
View Solution
