A car of mass m is driven with acceleration a along a straight level road against a constant external resistive force R. When the velocity of the car V, the rate at which the engine of the car is doing work will be
RV
maV
(R+ma)V
(ma-R)V
The correct Answer is:C
To solve the problem, we need to determine the rate at which the engine of the car is doing work when it is moving with a certain velocity V, given that it has a mass m, an acceleration a, and is facing a resistive force R.
1. Identify the Forces Acting on the Car:
- The car is driven by an engine force F in the direction of motion.
- There is a resistive force R acting in the opposite direction.
2. Apply Newton's Second Law:
- According to Newton's second law, the net force acting on the car is equal to the mass of the car multiplied by its acceleration:
Fnet=ma
- The net force can also be expressed as:
Fnet=F−R
- Setting these two expressions for net force equal gives:
F−R=ma
3. Solve for the Engine Force F:
- Rearranging the equation gives:
F=ma+R
4. Calculate the Power Delivered by the Engine:
- The power P delivered by the engine is given by the product of the force exerted by the engine and the velocity of the car:
P=F⋅V
- Substituting the expression for F from step 3 into this equation gives:
P=(ma+R)⋅V
5. Final Expression for Power:
- Thus, the rate at which the engine of the car is doing work is:
P=(ma+R)V
Conclusion:
The rate at which the engine of the car is doing work is given by:
P=(ma+R)V
- The car is driven by an engine force F in the direction of motion.
- There is a resistive force R acting in the opposite direction.
- According to Newton's second law, the net force acting on the car is equal to the mass of the car multiplied by its acceleration:
Fnet=ma
- The net force can also be expressed as:
Fnet=F−R
- Setting these two expressions for net force equal gives:
F−R=ma
- Rearranging the equation gives:
F=ma+R
- The power P delivered by the engine is given by the product of the force exerted by the engine and the velocity of the car:
P=F⋅V
- Substituting the expression for F from step 3 into this equation gives:
P=(ma+R)⋅V
- Thus, the rate at which the engine of the car is doing work is:
P=(ma+R)V
The rate at which the engine of the car is doing work is given by:
P=(ma+R)V
Topper's Solved these Questions
Similar Questions
A car starts from rest and moves with uniform acceleration a on a straight road from time t=0 to t=T. After that, a constant deceleration brings it to rest. In this process the average speed of the car is
View SolutionA car starts from rest and moves with uniform acceleration a on a straight road from time t=0 to t=T. After that, a constant deceleration brings it to rest. In this process the average speed of the car is
View SolutionA car of mass m is accelerating on a level smooth road under the action of a single F. The power delivered to the car is constant and equal to P. If the velocity of the car at an instant is v, then after travelling how much distance it becomes double?
 . View Solution
. View SolutionThe velocity-time graph of a car moving along a straight road is shown in figure. The average velocity of the car is first 25 seconds is
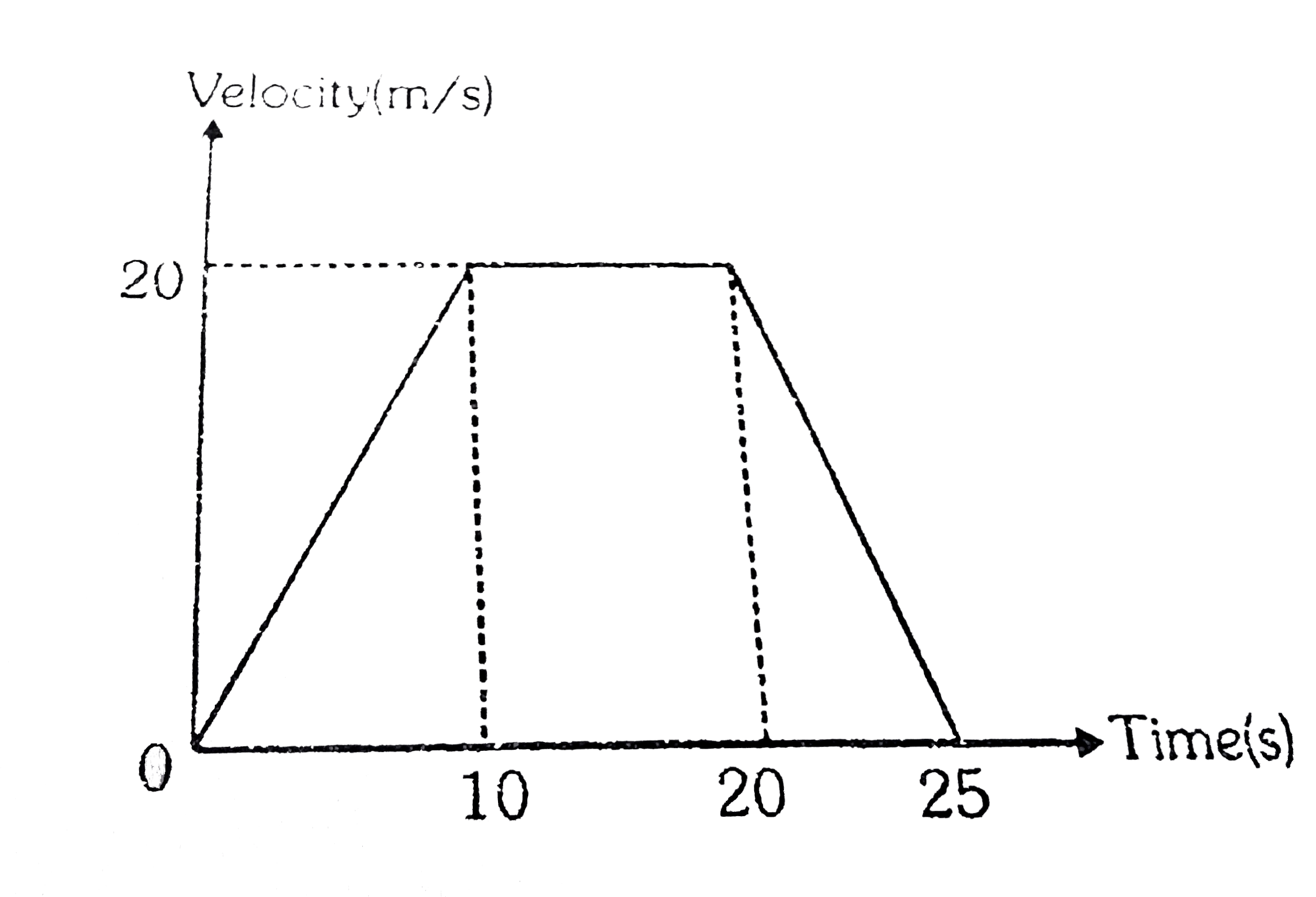 View Solution
View SolutionThe velocity-time graph of a car moving along a straight road is shown in figure. The average velocity of the car in first 25 seconds is
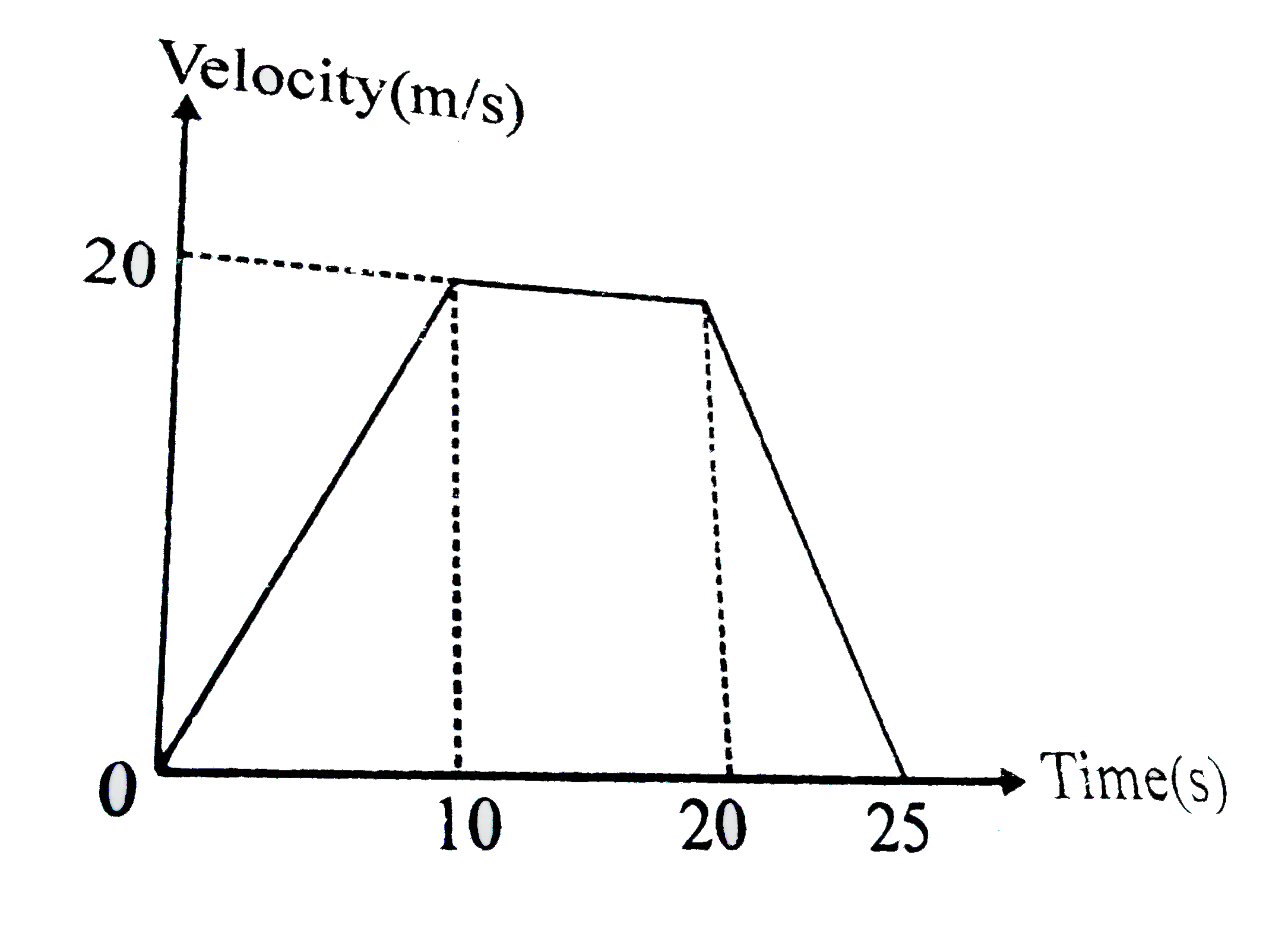 View Solution
View Solutiona. A rail road car of mass M is moving without friction on a straight horizontal track with a velocity ct. A man of mass m lands on it normally from a helicopter. What will be the new velocity of the car? ltbgt b. If now the man begins to run on it with speed um with respect to car in a direction opposite to motion of the car, what will be the new velocity of the car?
View SolutionA car drives along a straight level frictionless road by an engine delivering constant power. Then velocity is directly proportional to
View SolutionA car of mass M is accelerating on a level smooth road under the action of a single force F acting along the direction of motion. The power delivered to the car is constant and equal to p. If the velocity of the car at an instant is v, then after travelling a distance of 7Mv33p the velocity become kv where k is__________.
View SolutionA car moves in a straight line, the car accelerates from rest with a constant acceleraation α on a straight foad. After gaining a velocity v, the car moves with that velocity for somerime. Then car decelerates with a retardation β, If the total distance covered by the car is equal to s find the total time of its motion.
View Solutiona. A rail road flat car of mass M can roll without friction along a straight horizontal track . Initially, a man of mass m is standing on the car which is moving to the right with speed v0. What is the change in velocity of the car if the man runs to the left so that his speed relative to the car is vrel just before he jumps off at the left end?
b. If there are n men each of mass m on the car, should they all run and jump off together or should they run and jump one by one in order to give a greater velocity to the car?
 View Solution
View Solution

