The numuerical value of the ratio of instantaneous velocity to instantaneous spedd is.
Always less than 1
Always equal to 1
Always more than 1
Equal to or less than 1
The correct Answer is:B
To solve the question regarding the numerical value of the ratio of instantaneous velocity to instantaneous speed, we will follow these steps:
1. Understanding Instantaneous Velocity and Instantaneous Speed:
- Instantaneous velocity is defined as the rate of change of displacement with respect to time. It is a vector quantity, which means it has both magnitude and direction.
- Instantaneous speed, on the other hand, is the magnitude of instantaneous velocity. It is a scalar quantity and does not have a direction.
2. Mathematical Representation:
- The instantaneous velocity V(t) can be expressed mathematically as:
V(t)=limΔt→0x(t+Δt)−x(t)Δt
- The instantaneous speed S(t) is simply the magnitude of the instantaneous velocity:
S(t)=|V(t)|
3. Finding the Ratio:
- The ratio of instantaneous velocity to instantaneous speed can be expressed as:
Ratio=V(t)S(t)=V(t)|V(t)|
- Since V(t) can be positive or negative (depending on the direction of motion), the magnitude |V(t)| will always be positive.
4. Evaluating the Ratio:
- If V(t) is positive, the ratio becomes:
V(t)|V(t)|=V(t)V(t)=1
- If V(t) is negative, the ratio becomes:
V(t)|V(t)|=V(t)−V(t)=−1
- However, since we are looking for the numerical value of the ratio, we consider the absolute values.
5. Conclusion:
- Regardless of the direction of the instantaneous velocity, the absolute value of the ratio of instantaneous velocity to instantaneous speed is always:
Ratio=1
Final Answer:
The numerical value of the ratio of instantaneous velocity to instantaneous speed is 1.
- Instantaneous velocity is defined as the rate of change of displacement with respect to time. It is a vector quantity, which means it has both magnitude and direction.
- Instantaneous speed, on the other hand, is the magnitude of instantaneous velocity. It is a scalar quantity and does not have a direction.
- The instantaneous velocity V(t) can be expressed mathematically as:
V(t)=limΔt→0x(t+Δt)−x(t)Δt
- The instantaneous speed S(t) is simply the magnitude of the instantaneous velocity:
S(t)=|V(t)|
- The ratio of instantaneous velocity to instantaneous speed can be expressed as:
Ratio=V(t)S(t)=V(t)|V(t)|
- Since V(t) can be positive or negative (depending on the direction of motion), the magnitude |V(t)| will always be positive.
- If V(t) is positive, the ratio becomes:
V(t)|V(t)|=V(t)V(t)=1
- If V(t) is negative, the ratio becomes:
V(t)|V(t)|=V(t)−V(t)=−1
- However, since we are looking for the numerical value of the ratio, we consider the absolute values.
- Regardless of the direction of the instantaneous velocity, the absolute value of the ratio of instantaneous velocity to instantaneous speed is always:
Ratio=1
The numerical value of the ratio of instantaneous velocity to instantaneous speed is 1.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Graphical Concept17videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Graphical cancept1videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Subjective29videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer9videos
KINEMATICS-2
Similar Questions
A particle is moving with a constant speed in a circular path. Find the ratio of average velocity to its instantaneous velocity when the particle rotates an angle θ=(π2) .
View SolutionInstantaneous source of energy is
View SolutionInstantaneous source of energy is
View SolutionAssertion: Average speed of a particle in a given time interval is never less than the magnitude of the average velocity.
Reason: The magnitude of the velocity (instantaneous velocity) of a particle is equal to its speed.View SolutionHow is average velocity different from instantaneous velocity ?
View SolutionThe variation of the instantaneous current (I) and the instantaneous e.m.f (E) in a circuit is as shown in figure. Which of the following statement is correct?
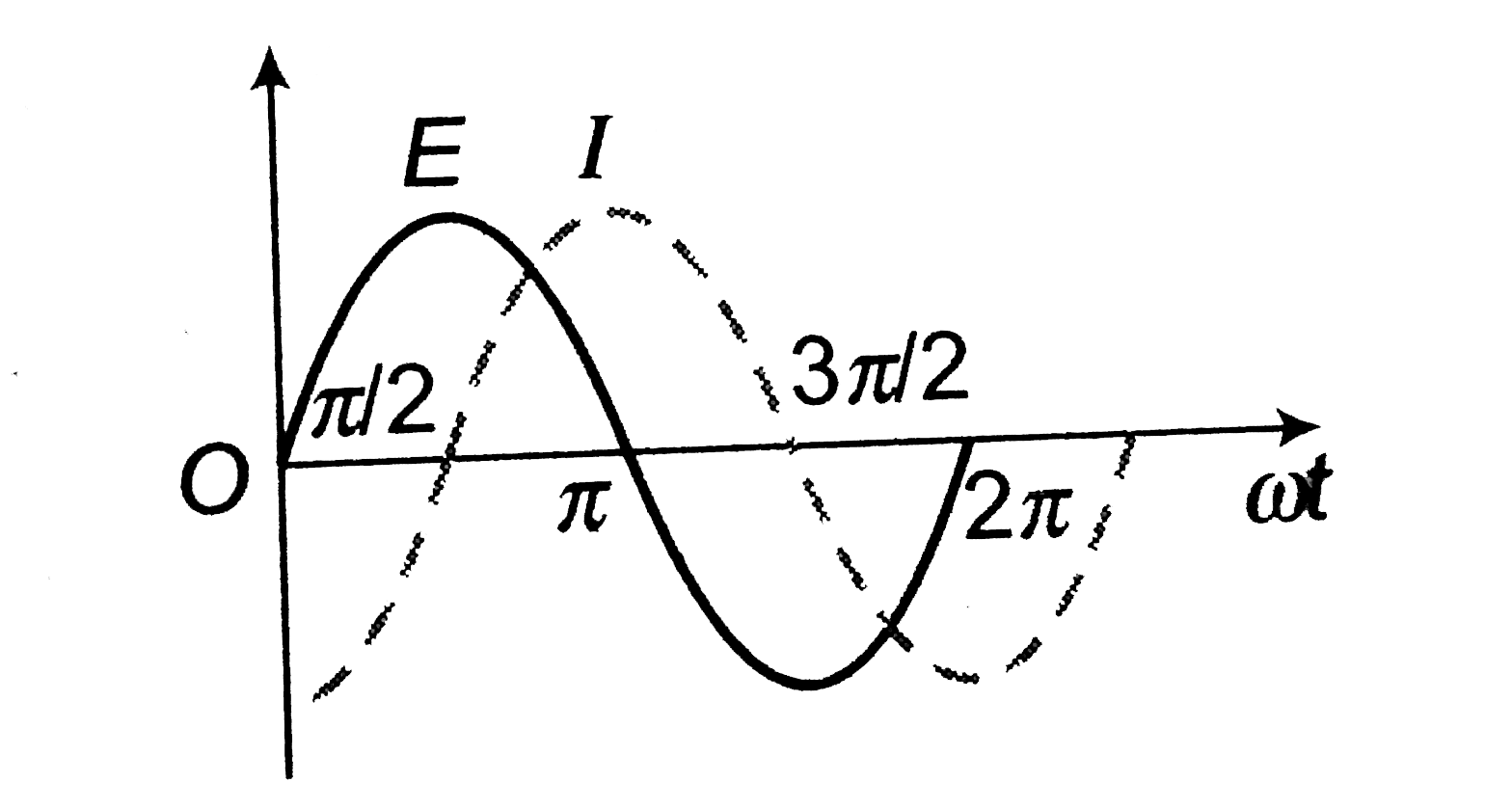 View Solution
View SolutionStatement I: The average velocity of the body may be equal to its instantaneous velocity.
Statement II: For a given time interval of a given motion, average veocity is single valued while average speed can have many values.View SolutionA spaceship in space sweeps stationary interplanetary dust . As a result , its mass increase at a rate dM(t)dt=bv2(t) , where v(t) is its instantaneous velocity . The instantaneous acceleration of the satellite is :
View SolutionWhen a particle moves with constant velocity, its average velocity, its instantaneous velocity and its speed are all equal. Comment on this statement.
View SolutionWhen a particle moves with constant velocity its average velocity, its instantaneous velocity and its speed all are equal. Is this statement true or false ?
View Solution

