A juggler throws balls into air. He throws one when ever the previous one is at its highest point. If he throws n balls each second, the height to which each ball will rise is
5m
3,75m
2.50m
1.25m
The correct Answer is:A
Time of ascent=1⇒ug=⇒u=10msd−1
Maximum height attained =u22g=1022×10=5.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Graphical Concept17videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Graphical cancept1videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Subjective29videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer9videos
KINEMATICS-2
Similar Questions
A juggler throws ball into air. He throus one whenever the previus one is at its highest point. How high do the balls rise if he throus (n) balls each second. Acceleration the to gravity=g.
View SolutionA boy throws a ball in air in such a manner that when the ball is at its maximum height he throws another ball. If the balls are thrown with the time difference 1 second, the maximum height attained by each ball is
View Solution
Knowledge Check
- Question 1 - Select One
A man throw rings into air one after the other at an interval of one second. The next ring is thrown when the velocity of the ring thrown earlier is zero. The height to which the ring rise is (takeg=10ms−2)
A15 mB5 mC10 mD20 m - Question 2 - Select One
A player throws a ball vertically upwards with velocity u. At highest point,
A1. both the velocity and acceleration of the ball are zero.B2. the velocity of the ball is u but its accelerationC3. the velocity of the ball is zero but its acceleration is g.D4. the velocity of the ball is u but its acceleration is g.
A person throws balls into the air one after the other at an interval ofone second. The next ball is thrown when the velocityof the ball thrown earlier is zero. To what height the ball rise:
View SolutionA cricket fielder can throw the cricket ball with a speed v0.If the throws the ball while running with speed u at an angle θ to the horizontal.
The effective angle to the horizontal at which the ball is projected in air as seen by a spectator isView SolutionA boy throws balls into air at regular interval of 2 second. The next ball is thrown when the velocity of first ball is zero. How high do the ball rise above his hand? [Take g=9.8m/s2]
View SolutionIn quick succession, a large number of balls are thrown up vertically in such a way that the next ball is thrown up when the previous ball is at the maximum height. If the maximum height is 5m, then find the number of the balls thrown up per second (g=10 m s^(-2)).
View SolutionTwo rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.
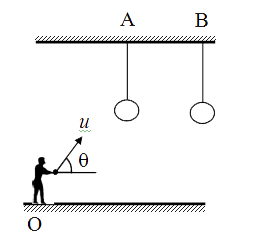
The maximum height attained by the ball above the floor is:View SolutionTwo rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.
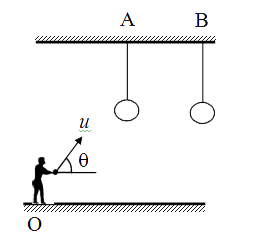
When the ball lands on the floor, the stop watch reads:View Solution

