A large , heavy box is sliding without friction down a smooth plane of inclination . From a point on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is , and the direction of projection makes an angle with the bottom as shown in Figure .
(a) Find the distance along the bottom of the box between the point of projection and the point where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .)
(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected .

Method 1 : (a) is the relative velocity of the particle with respect to the box. Resolve .
Let is the relative velocity of the particle with respect to the box in x - direction. Let is the relative velocity with respect to the box in y - direction.
y - direction motion(taking relative terms w.r.t. box)
or
x - direction motion (taking relative terms w.r.t. box) :
(b) For the observer (on ground) to see the horizontal displacement to be zero, the distance travelled by the box in time should be equal to the range of the particle. Let the speed of the box at the time of projection of particle be . Then for the motion of box with respect to ground (Fig. 5.176).
Put the values of and solve to get
Method 2 : The above condition can be met if the box covers exactly the same distance as the range of particle.
or
or .
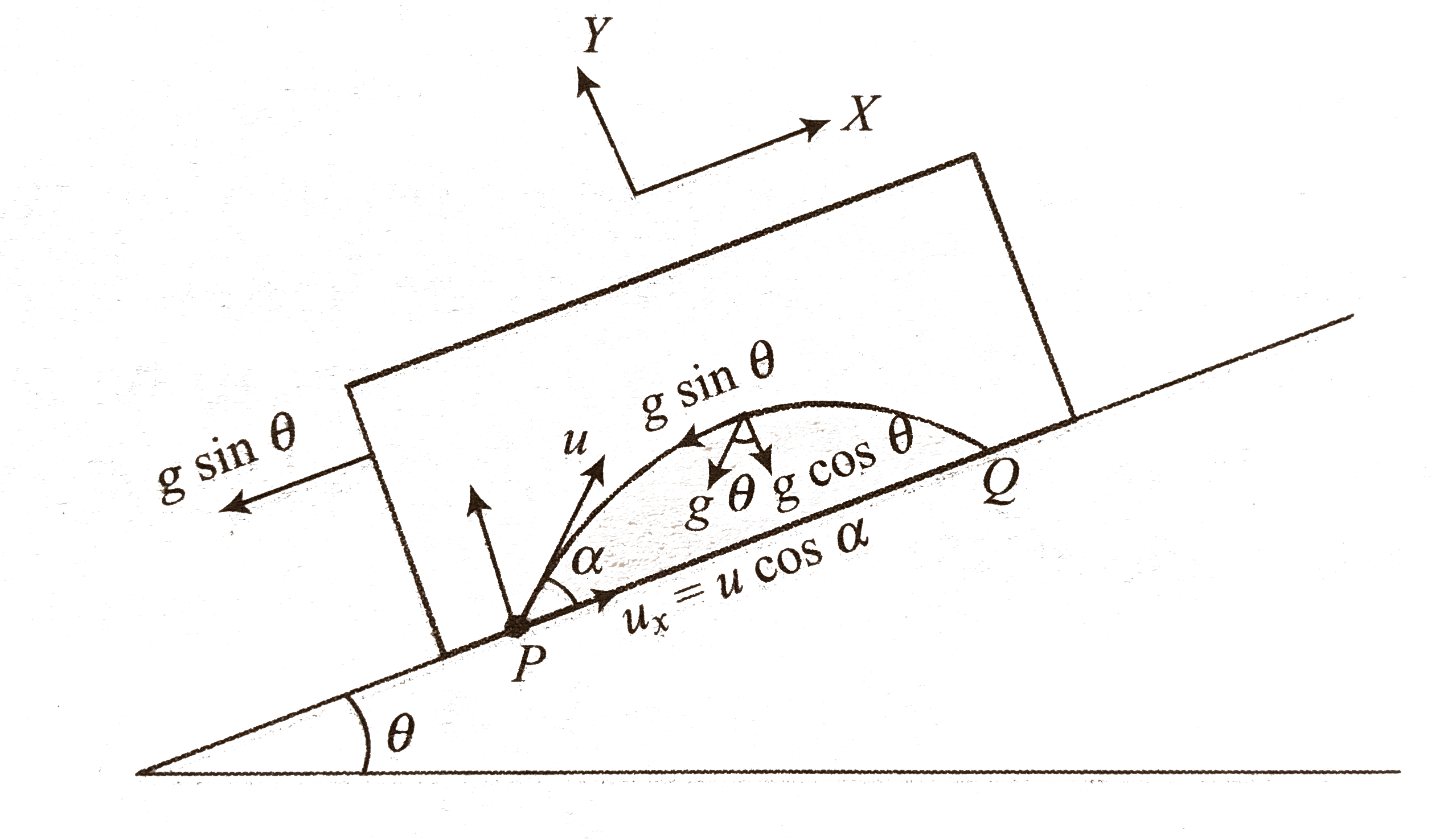 ,
,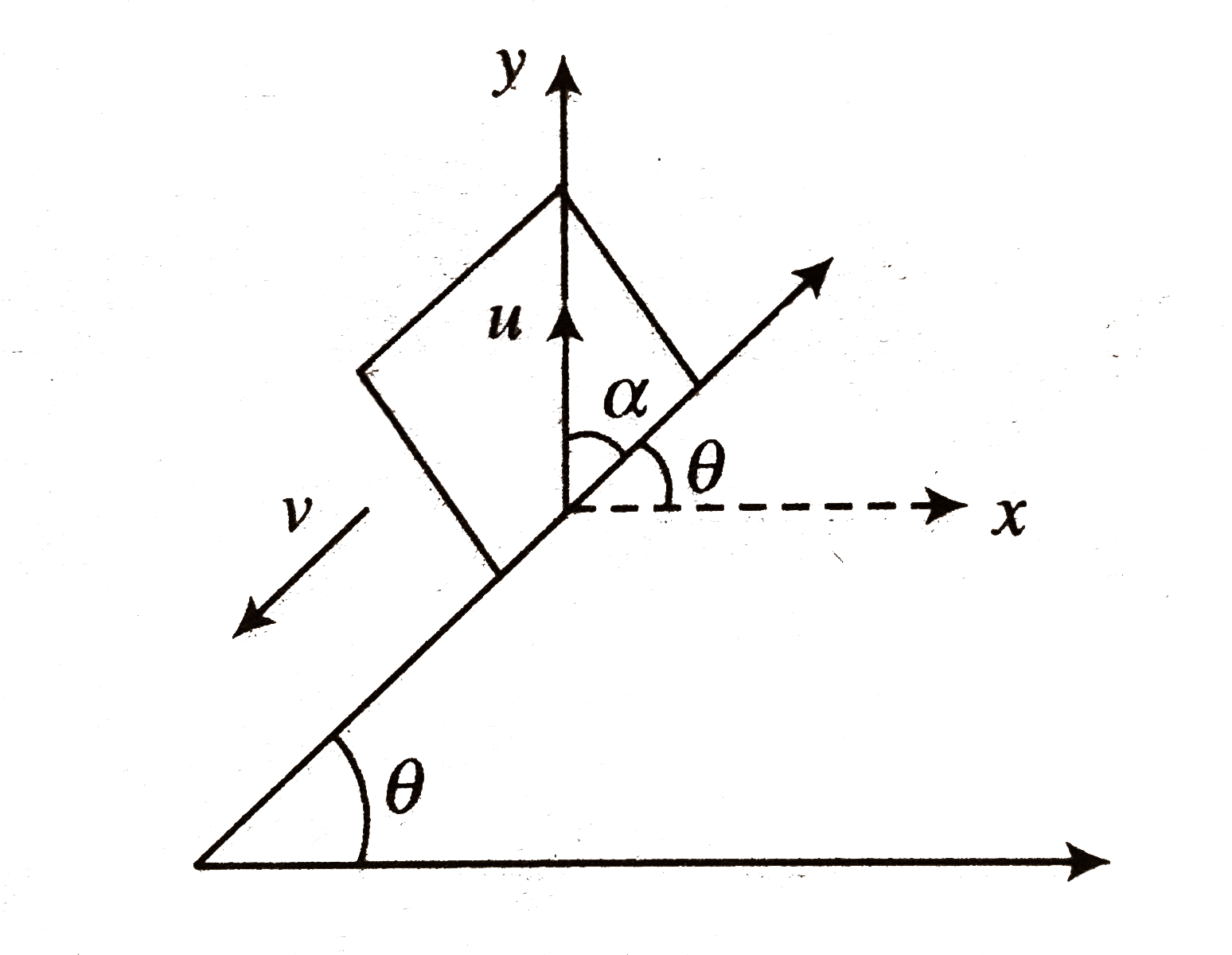 .
.
Topper's Solved these Questions
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise 5.1
Explore 15 Videos
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise 5.2
Explore 25 Videos
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Integer
Explore 9 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
Similar Questions
Knowledge Check
in the question number 4, if the horizontal displacement of the particle as seen by an observer on the ground is zero, the speed of the box with respect to the ground at the instant when particle was projected is
AucosαBusinαcosθCucos(α+θ)cosθDusinθsinαcosθin the question number 4, if the horizontal displacement of the particle as seen by an observer on the ground is zero, the speed of the box with respect to the ground at the instant when particle was projected is
AucosαBusinαcosθCucos(α+θ)cosθDusinθsinαcosθA particle is projected with a speed u at an angle θ with the horizontal. What will be the speed of the particle when direction of motion of particle is at an angle α with the horizontal?
AucosθsecαBusecθcosαCucosθtanαDucosθcotα
A rectangular box is sliding on a smooth inclined plane of inclination θ. At t=0 the box starts to move on the inclined plane. A bolt starts to fall from point A. Find the time after which bolt strikes the bottom surface of the box.
View SolutionA particle slides down on a smooth incline of inclination 30∘, fixed in an elevator going up with an acceleration 2m/s2. The box of incline has width 4m. The time taken by the particle to reach the bottom will be

View SolutionA box is failing freely. Inside the box, a particle is projected with some velocity v with respect to the box at an angle θ as shown in the figure.

View SolutionA particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .
.
View SolutionA particle slides down on a smooth incline of inclination 30∘, fixed in an elevator going up with an acceleration 2m/s2. The box of incline has width 4m. The time taken by the particle to reach the bottom will be

View Solution
