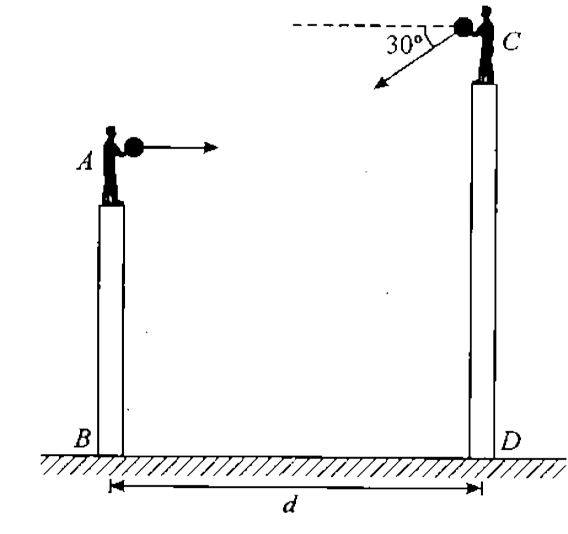
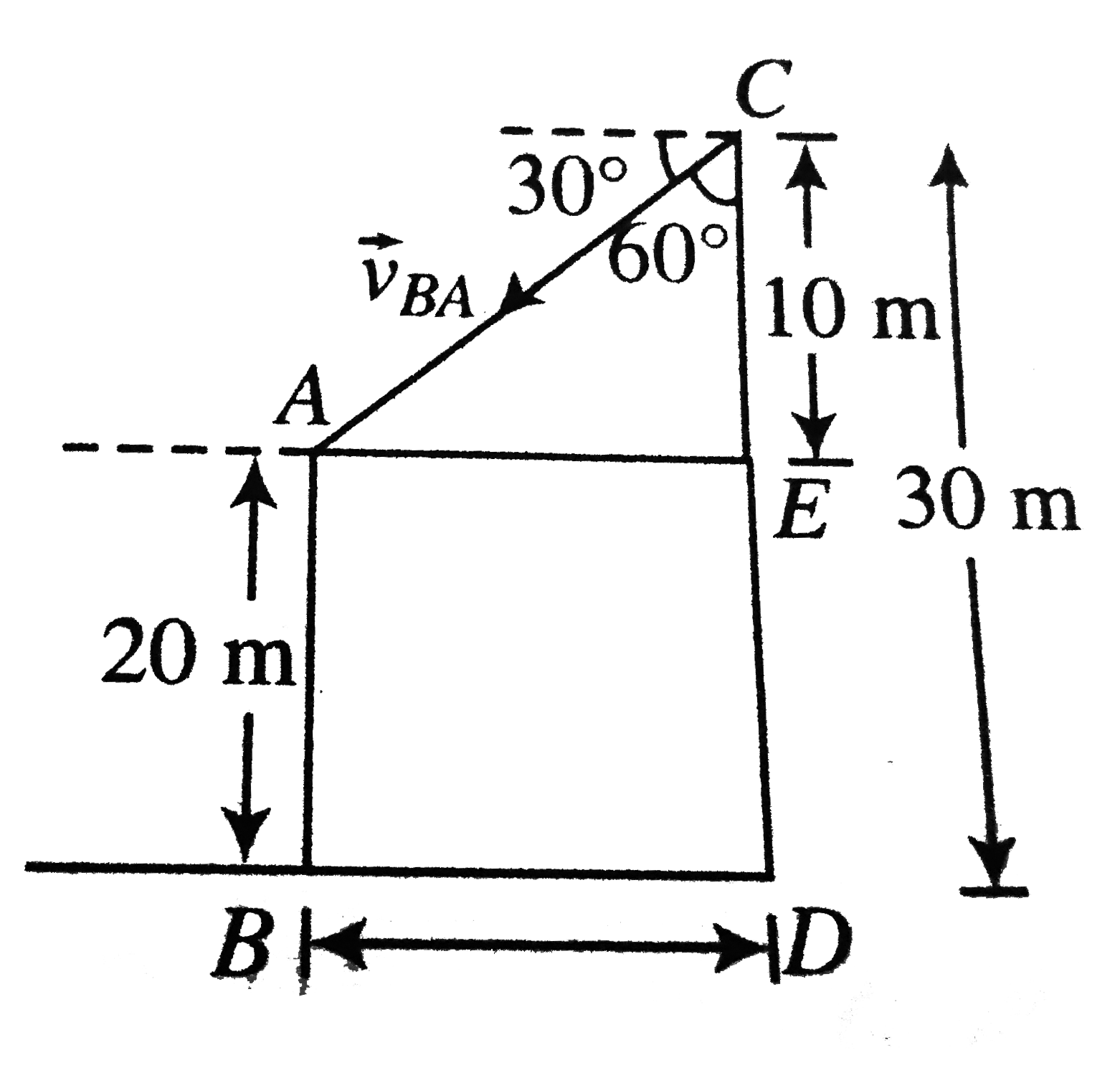
Two towers AB and CD are situated at a distance d apart, as shown in figure. AB is 20 m high and CD is 30 m high from the ground. An object of mass m is thrown from the top of AB horizontally with a velocity of 10 m/s towards CD. Simultaneously another object of mass 2 m is thrown fromt the top of CD at an angle of 60∘ to the horizontal towards AB with the same magnitude of initial velocity as that oft he first object. The two objects move in the same vertical plane, collide in mid air and stick to each other (i) calculate the distance between the towers and (ii) find the position where the objects hit the ground.
Method 1 : (a) Let t be the time taken for collision. For mass m thrown horizontally from A for horizontal motion,
PM=10t …(i)
For vertical motion, uy=0,sy=y,ay=g
Sy=uyt+12ayt2⇒y=12gt2...(ii)
vy=uy+ayt=gt ...(iii)
From mass 2m thrown from C, for horizontal motion
QM=[10cos60∘]t⇒QM=5t ...(iv)
For vertical motion : uy=10sin60∘=5√3)
⇒vy=5√3)+gt ...(v)
ay=g.Sy=y+10,S=ut+12at2
⇒y+10=s√3t+12gt2 ...(vi)
From (ii) and (vi), 12gt2+10=s√3t+12gt2⇒t=2√3s
BD=PM+MQ
=10t+5t
=15t=15×2√3
=10√3=17.32m
(b) Applying the conservation of linear momentum (during collision of the masses at M) in the horizontal direction, we have
m×10−2m10cos60∘
=3m×vx⇒10m−10m=3m×vx⇒vx=0
Since the horizontal momentum comes out to be zero, the combination of masses will drop vertically downwards
and fall at E,BE=PM=10t=10×3√3=11.547m
Method 2 : Acceleration of AandC both is 9.8ms−2 downward.
Therefore, the relative acceleration between them is zero, i.,e., the relative motion between them will be a straight line.
Now assuming A to be at rest, the condition of collision will be that →vCA=→vC−→vA = relative velocity of Cw.r.t.A should be along CA
→vA=10ˆi
→vB=−5ˆi−5√3ˆj
→vBA=−5ˆi−5√3ˆj−10ˆi∴→vBA=−15ˆi−5√3ˆj
∴tan60∘=d10ord=10√3m.
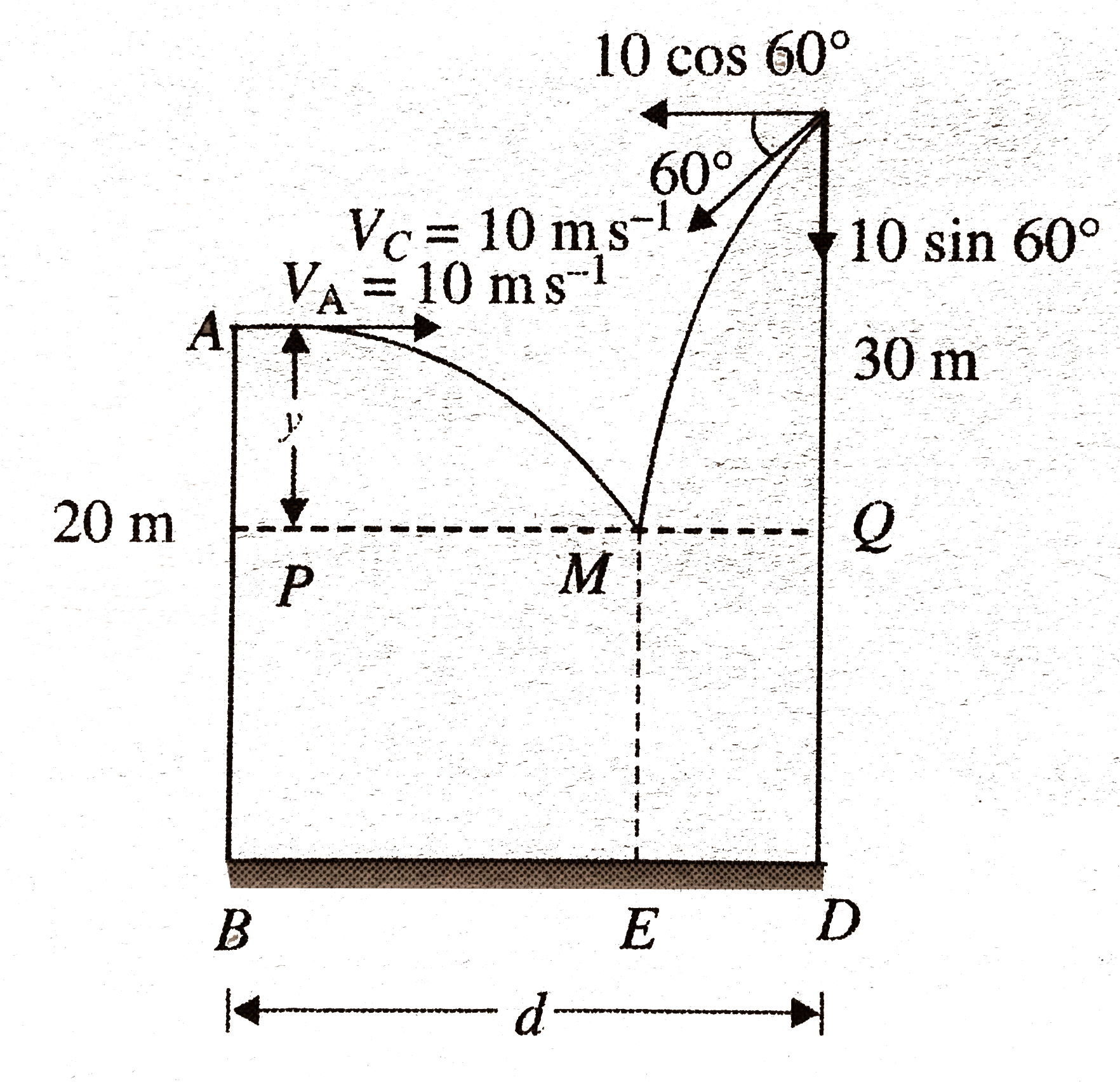 ,
,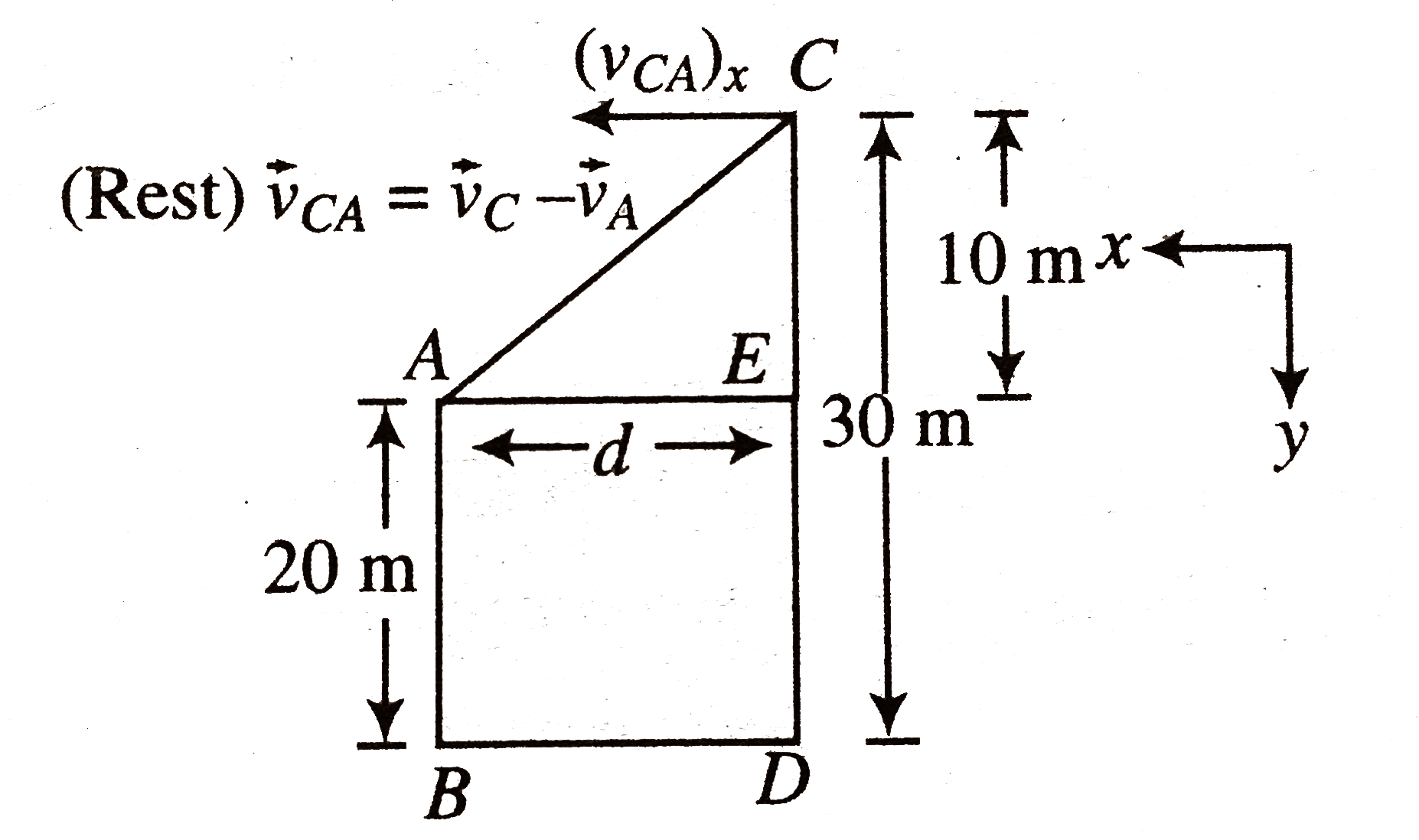 ,
,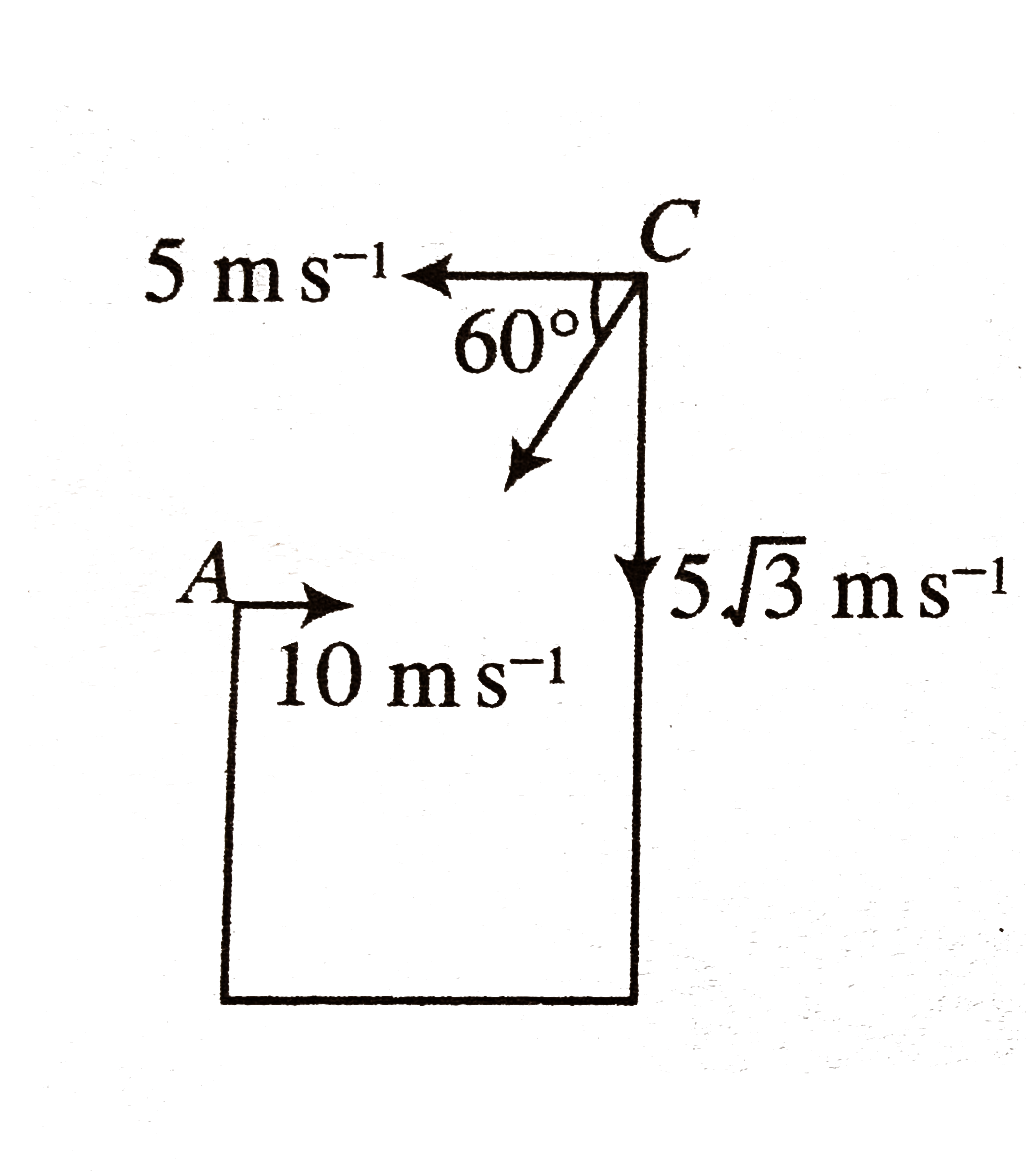 ,
, .
.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.1
15 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.2
25 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
Two towers AB and CD are situated at a distance d apart, as shown in figure. AB is 20 m high and CD is 30 m high from the ground. An object of mass m is thrown from the top of AB horizontally with a velocity of 10 m/s towards CD. Simultaneously another object of mass 2 m is thrown fromt the top of CD at an angle of 60∘ to the horizontal towards AB with the same magnitude of initial velocity as that oft he first object. The two objects move in the same vertical plane, collide in mid air and stick to each other (i) calculate the distance between the towers and (ii) find the position where the objects hit the ground.

View SolutionTwo towers AB and CD are situated a distance d apart as shown in figure. AB is 20 m high and CD is 30 m high from the ground. An object of mass m is thrown from the top of AB horizontally with a velocity of 10 m/s towards CD. Simultaneously another object of mass 2 m is thrown from the top of CD at an angle 60∘ below the horizontal towards AB with the same magnitude of initial velocity as that of the first object. The two objects move in the same vertical plane, collide in mid-air and stick to each other.

Calculate the distance d between the towers.
View Solution
Knowledge Check
A ball of mass m is thrown at an angle of 45∘ to the horizontal,, from the top of a 65m high tower AB as shown in Fig. at t=0. Another identical ball is thrown with velocity 20m/s horizontally towards AB from the top of a 30m high tower CD1s after the projection of the first ball. Both the balls move the same vertical plane. If they collide in mid-air,

the distance AC isA20mB30mC40mD20m
Two towers AB and CD are situated a distance d apart as: shown in Fig. 1E.139 (a). AB is 20 m high and CD is 30 m high from the ground. An object of mass mis thrown from the top of AB horizontally with a velocity of 10 m/s towards CD.
Simultaneously another object of mass 2m is thrown from the ·top of CD at an angle of 60∘ to the horizontal towards AB with the same magnitude of initial velocity as that of the_ first' objects . The two objects move in the same vertical plane, collide in mid-air and stick to each other.
Calculate the distance d between the towers.
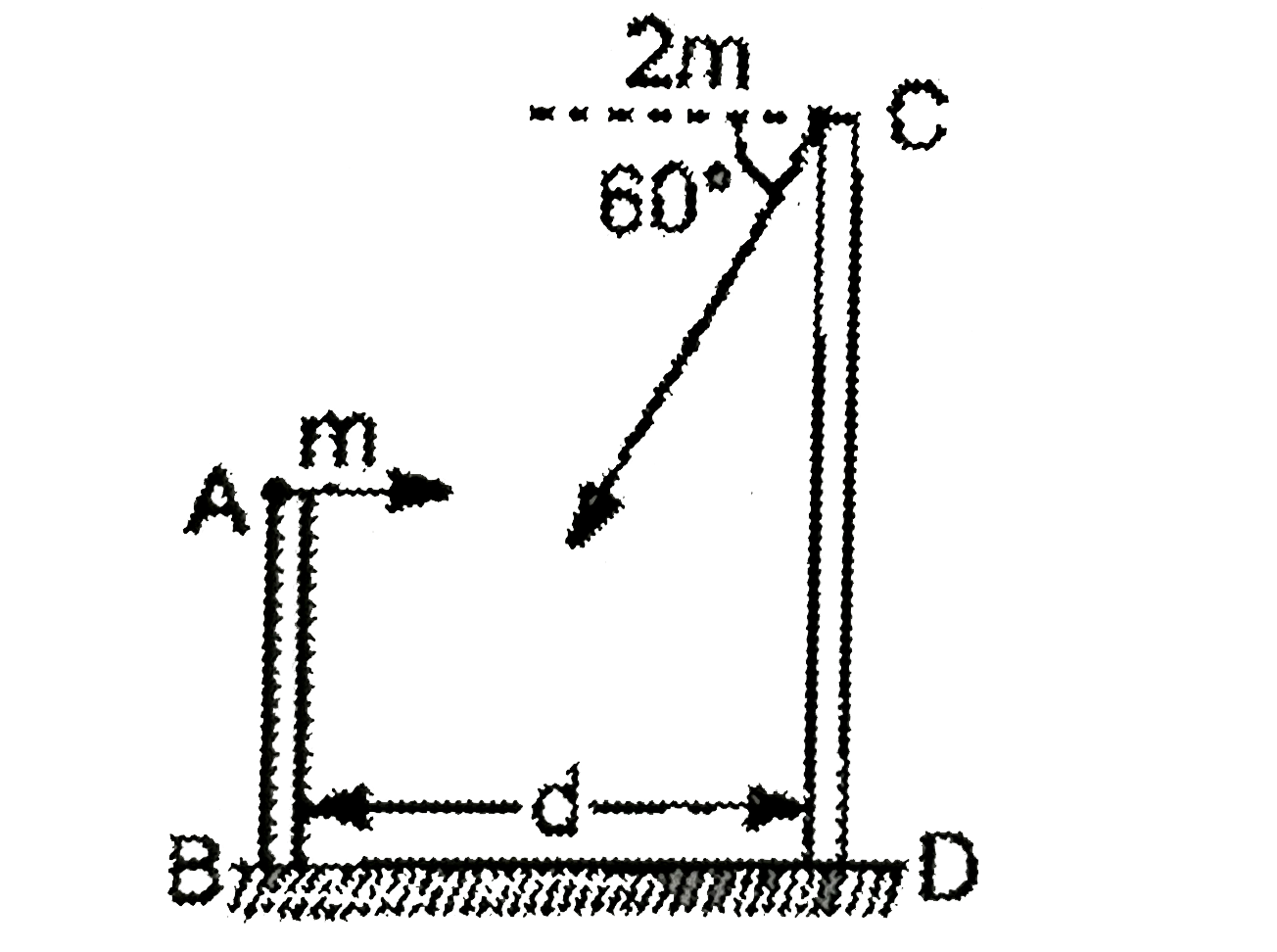
View SolutionTwo towers AB and CD are situated a distance d apart as shown in Fig. 5.45. AB is 20m high and
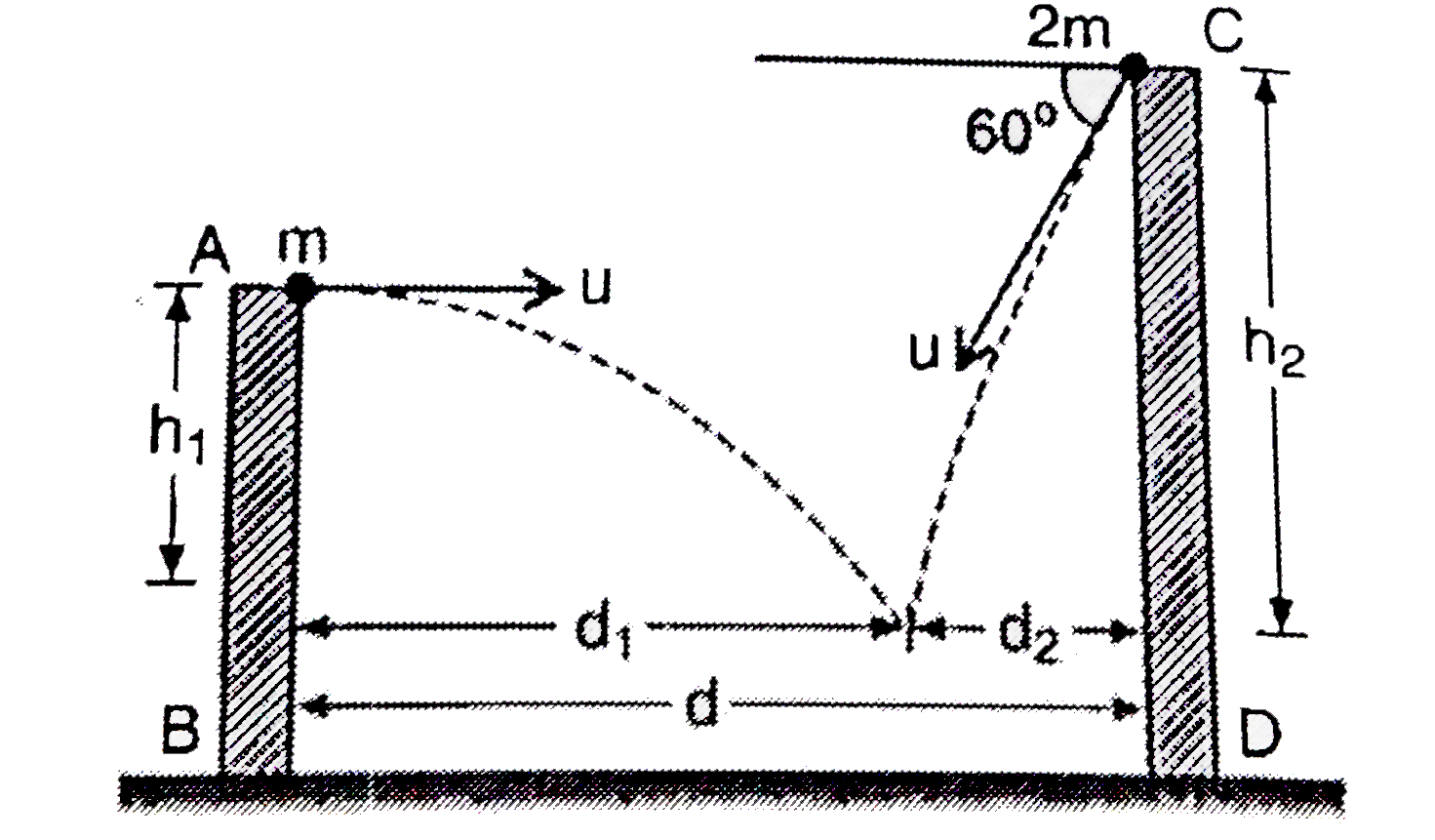
CD is 30m highfrom the ground . An object of mass m is thrown from the top of AB horizontally with a velocity 10m/s towards CD. simu ltaneously another object of mass 2 m is thrown from the top of CD at an angle of 60∘ to the horizotnal towards AB with the same magnitude of initial velocity as that of the first object. the two objects move in the same vertical plane, clollide in mid air and stick to each other, (a) Calcu late the distance d between the towers and (b) fin the position where the objects hit the ground.
View SolutionTwo towers AB and CD are situated a distance d apart as shown in figure. AB is 20 m high and CD is 30 m high from the ground. An object of mass m is thrown from the top of AB horizontally with a velocity of 10 m/s towards CD. Simultaneously another object of mass 2 m is thrown from the top of CD at an angle 60∘ below the horizontal towards AB with the same magnitude of initial velocity as that of the first object. The two objects move in the same vertical plane, collide in mid-air and stick to each other.

Find the distance from B where the objects hit the ground.
View SolutionA ball of mass m is thrown at an angle of 45∘ to the horizontal,, from the top of a 65m high tower AB as shown in Fig. at t=0. Another identical ball is thrown with velocity 20m/s horizontally towards AB from the top of a 30m high tower CD1s after the projection of the first ball. Both the balls move the same vertical plane. If they collide in mid-air,

the distance AC is
View SolutionA particle of mass m is thrown horizontally from the top of a tower and anoher particle of mass 2m is thrown vertically upward. The acceleration of centre of mass is
View SolutionA particle of mass m is thrown horizontally from the top of a tower and anoher particle of mass 2m is thrown vertically upward. The acceleration of centre of mass is
View SolutionA particle of mass m is thrown horizontally from the top of a tower and anoher particle of mass 2m is thrown vertically upward. The acceleration of centre of mass is
View Solution
