A man directly crosses a river in time t1 and swims down the current a distance equal to the width of the river I time t2. If uandv be the speed of the current and the man respectively, show that : t1:t2=√v+u:√v−u).
To solve the problem, we need to analyze the motion of a man crossing a river and swimming downstream. Let's break it down step by step.
Step 1: Define the variables
Let:
- d = width of the river
- u = speed of the current
- v = speed of the man in still water
- t1 = time taken to cross the river directly
- t2 = time taken to swim downstream a distance equal to the width of the river
Step 2: Calculate time t1
When the man swims directly across the river, he must swim at an angle to counteract the current. The effective velocity of the man across the river can be calculated using the Pythagorean theorem. The effective velocity veff when swimming directly across is given by:
veff=√v2−u2
This is because the man's velocity v and the current's velocity u form a right triangle where v is the hypotenuse.
The time taken t1 to cross the river is:
t1=dveff=d√v2−u2
Step 3: Calculate time t2
When the man swims downstream, his effective velocity is the sum of his swimming speed and the current speed:
vdownstream=v+u
The time taken t2 to swim downstream a distance equal to the width of the river is:
t2=dv+u
Step 4: Find the ratio t1t2
Now we can find the ratio of the two times:
t1t2=d√v2−u2dv+u=v+u√v2−u2
Step 5: Simplify the expression
We know that:
√v2−u2=√(v+u)(v−u)
Substituting this into our ratio gives:
t1t2=v+u√(v+u)(v−u)
This can be simplified further:
t1t2=√v+u√v−u
Conclusion
Thus, we have shown that:
t1t2=√v+u√v−u
Let:
- d = width of the river
- u = speed of the current
- v = speed of the man in still water
- t1 = time taken to cross the river directly
- t2 = time taken to swim downstream a distance equal to the width of the river
When the man swims directly across the river, he must swim at an angle to counteract the current. The effective velocity of the man across the river can be calculated using the Pythagorean theorem. The effective velocity veff when swimming directly across is given by:
When the man swims downstream, his effective velocity is the sum of his swimming speed and the current speed:
Now we can find the ratio of the two times:
We know that:
Thus, we have shown that:
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.4
11 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Subjective
40 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.2
25 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A man swims across a river with speed of Vm perpendicular to the flow direction of river. If the water flows with a speed Vw with what resullant velocity does the man cross the river ?
View SolutionA man in a boat crosses a river from point A. If he rows perpendicular to the banks he reaches point C (BC=120m) in 10 min. If the man heads at a certain angle α to the straight line AB (AB is perpendicular to the banks) against the current he reaches point B in 12.5 min. Find the width of the river w, the rowing velocity u, the speed of the river current v and the angle α. Assume the velocity of the boat relative to water to be constant and the same magnitude in both cases.

View SolutionA man can swim in still water at a speed of 4 kmph. He desires to cross a river flowing at a speed of 3 kmph in the shortest time interval. If the width of the river is 3km time taken to cross the river (in hours) and the horizontal distance travelled (in km) are respectively
View SolutionA man crosses the river perpendicular to river in time t seconds and travels an equal distance down the stream in T seconds. The ratio of man's speed in still water to the river water will be:
View SolutionA man wants to swim in a river from A→B and back from B→A always following line AB (Fig. 5.94). The distance between points AandB is S. The velocity of the river current v is constant over the entire width of the river. The line AB makes an angle ∝ with the direction of current. The man moves with velocity u at angle β to the line AB. The man swim to cover distance AB and back, find the time taken to complete the journey.
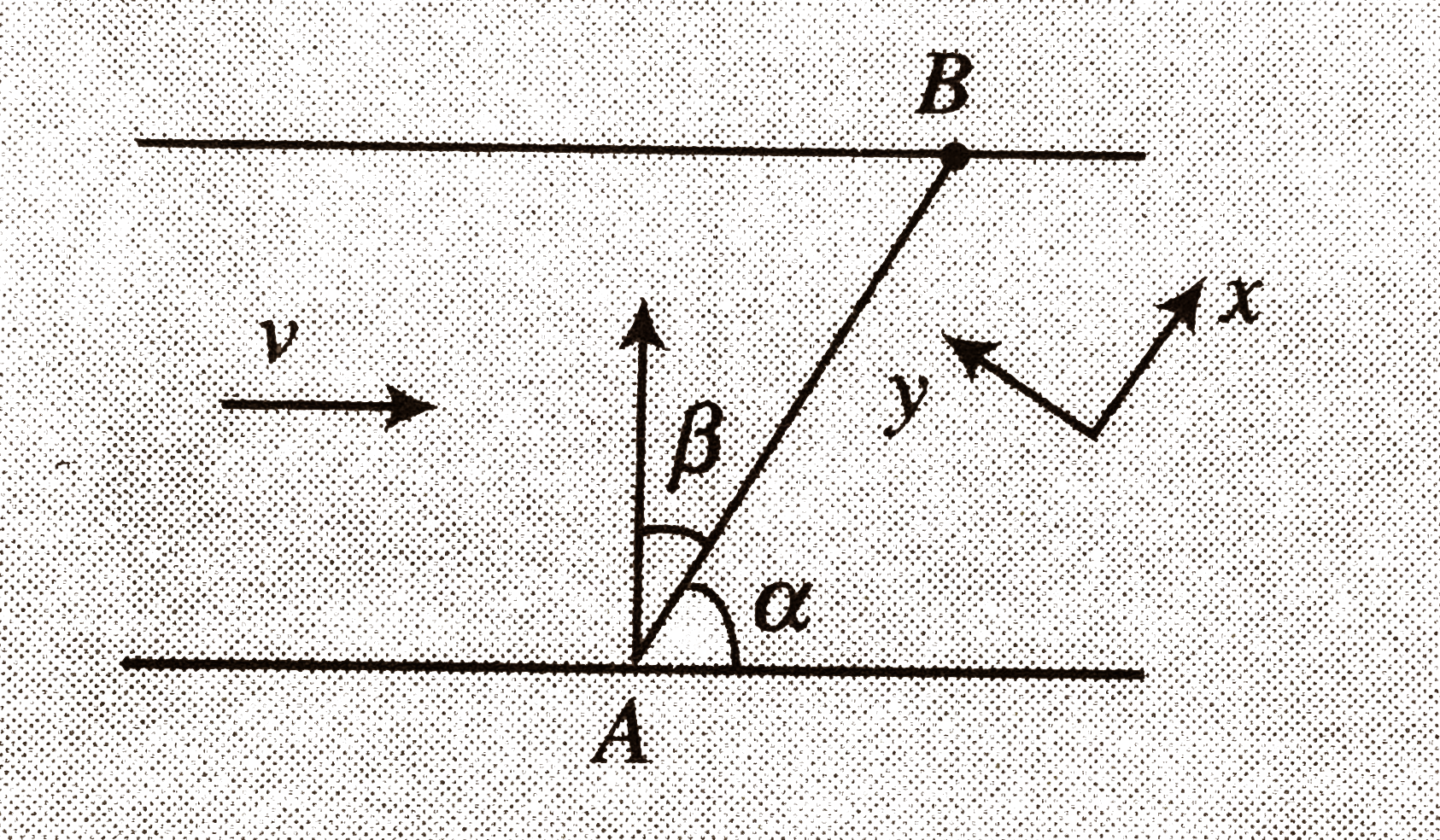 .
.
View SolutionThe ratio of downstream drift of a person in crossing a river making same angles with downstream and upstream are respectively 2 : 1. The ratio of the speed of river u and the swimming speed of person v is:
View SolutionA man can swim with speed u with respect to river. The widith of river is d. The speed of the river is zero at the banks and increses linearly to V0 till mid stream of the river then decreases to zero to the other bank. When man crosses the river in shoetest time, drift is equal to: (givenu>v0)
View SolutionIf velocity v varies with time(t) as v=2t−3, then the plot between v and t is best represented by :
View SolutionA ,man wishing to cross a river flowing with velocity u jumps at an angle θ with the river flow.
(a) Find the net velocity of the man with respect to ground if he can swim with speed v in still water.
(b) In what direction does the boat actually move ?
( c) Find how far from the point directly opposite to the starting point does the boat reach the opposite bank, if the width of the river is d.
View SolutionA swimmer crosses a flowing stream of width ω to and fro in time t1. The time taken to cover the same distance up and down the stream is t2. If t3 is the time the swimmer would take to swim a distance 2ω in still water, then
View Solution
