A man in a boat crosses a river from point A. If he rows perpendicular to the banks he reaches point C (BC=120m) in 10 min. If the man heads at a certain angle α to the straight line AB (AB is perpendicular to the banks) against the current he reaches point B in 12.5 min. Find the width of the river w, the rowing velocity u, the speed of the river current v and the angle α. Assume the velocity of the boat relative to water to be constant and the same magnitude in both cases.

The correct Answer is:A, B, C
In the first case, BC=vt1andw=ut1

In the second case,
usinα=vandw=(ucosα)t2
Solving these four equations with proper substitutions, we get
w=200m,
u=20m/min,
v=12m/min
and α=36∘50′
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - SCQ_TYPE
39 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - MCQ_TYPE
23 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Comprehension
7 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
A ball is hit by a batsman at an angle of 37∘ as shown in figure. The man standing at P should run at what minimum velocity so that he catches the ball before it strikes the ground. Assume that height of man is negligible in comparison to maximum height of projectile.

View SolutionIn a projectile motion let tOA=t1 and tAB=t2.The horizontal displacement from O to A is R1 and from A to B is R2.Maximum height is H and time of flight is T.If air drag is to be considered, then choose the correct alternative(s).
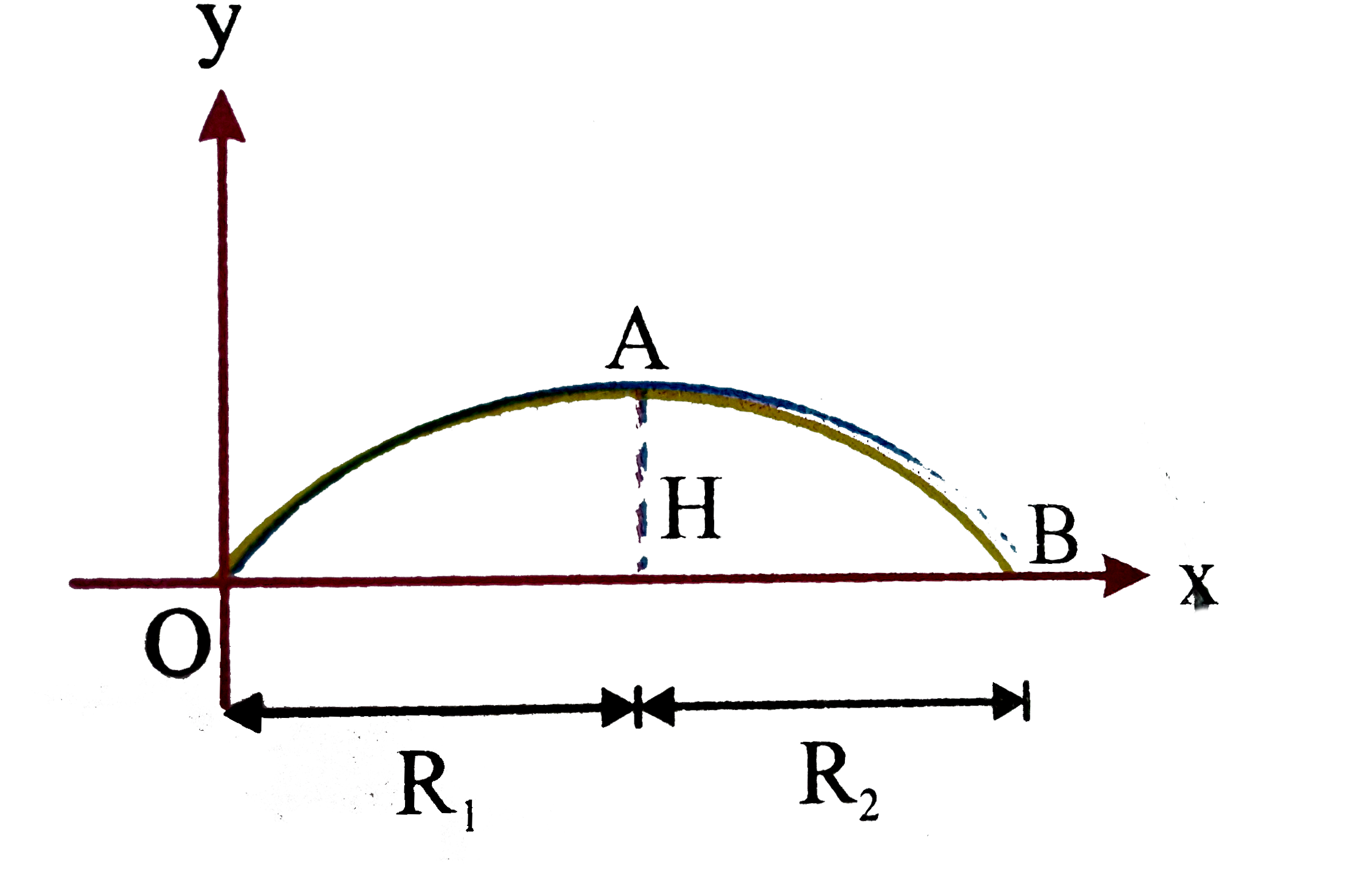
View SolutionAn elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
1. The time in which the ball strikes the floor of elevator is given by
View SolutionStarting from the centre of the earth having radius R, the variation of g (acceleration due to gravity) is shown by
View SolutionA stone is dropped from a certain height which can reach the ground in 5s. It is stopped after 3s of its fall and then it is again released. The total time taken by the stone to reach the ground will be .
View SolutionA man crosses a river in a boat. If he cross the river in minimum time he takes 10 min with a drift 120 m. If he crosses the river taking shortest path, he takes 12.5 min, find (a) width of the river (b) velocity of the boat with respect to water (c) speed of the current
View SolutionA man in a boat crosses a river from point A. If he rows perpendicular to the banks he reaches point C (BC=120m) in 10 min. If the man heads at a certain angle α to the straight line AB (AB is perpendicular to the banks) against the current he reaches point B in 12.5 min. Find the width of the river w, the rowing velocity u, the speed of the river current v and the angle α. Assume the velocity of the boat relative to water to be constant and the same magnitude in both cases.

View SolutionA man swims from a point A on the bank of a river if width 100 m . When he swims perpendicular to the water current, he reaches the other bank 50 m downstream. The angle to the bank at which he should swim, to reach the directly opposite point B on the other bank is. .
View SolutionA river is flowing steradily with a speed 5kmh−1 . A boat man can row with a speed of 10kmh−1 in still water. He rows his boat in river at right angles to the bank of river, If width of river is 800m, (i) how much time the boat man will take to cross the river ? (ii) How far away from a point just opposite to the bank of river he will be reaching there ? (ii) What will be his effective speed gt
View SolutionA man in a row boat must get from point A to point B on the opposite bank of the river (see figure).The distance BC=a .The width of the river AC=b .At what minimum speed u relative to the still water should the boat travel to reach the point B ?The velocity of flow of the river is v_(0)
View SolutionA man in a boat crosses a river from point A. if the rows perpendicu lar to the bank he reaches point C(BC=120m) in 10 minutes. If the the man heads at a certain angle alpha to the straight line AB(AB is perpendicualr to the banks) against the current be reaches point B in12.5 minutes.
View SolutionA man is boat intends to cross river from A. If he rows perpendicular to the banks then he takes t1 = 10 minutes to reach the other bank and he reaches point C at a distance l = 120 m down the stream from the point B which is exactly opposite to A on the other bank. If he heads at a certain angle α to the straight path AB against the current he will reach point B in t2 = 12.5 minutes.
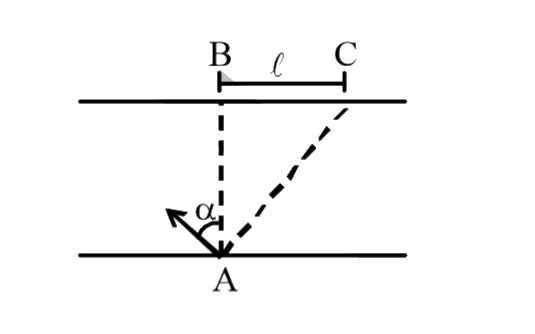
The width of river is-
View SolutionA man crosses a river in a boat. If he crosses the river in minimum time he takes 10 min with a drift 120 m . If he crosses the river taking the shortest path, he takes 12.5 min. what is the width of the river ?
View SolutionA man crosses a river in a boat. If he crosses the river in minimum time he takes 10 min with a drift 120 m . If he crosses the river taking the shortest path, he takes 12.5 min.
What is the velocity of the boat in still water ?
View SolutionA man crosses a river in a boat. If he crosses the river in minimum time he takes 10 min with a drift 120 m . If he crosses the river taking the shortest path, he takes 12.5 min.
What is the speed of the current ?
View Solution
