A ball is thrown from a point with a speed 'v^(0)' at an elevation angle of θ . From the same point and at the same instant , a person starts running with a constant speed 'v0'2 to catch the ball . Will the person be able to catch the ball ? If yes, what should be the angle of projection θ ?
Yes,60∘
Yes,30∘
No
Yes,45∘
The correct Answer is:A
To determine whether the person can catch the ball and at what angle of projection θ this can happen, we can analyze the motion of both the ball and the person.
1. Understand the Motion of the Ball:
The ball is thrown with an initial speed v0 at an angle θ. The horizontal and vertical components of the ball's velocity can be expressed as:
- Horizontal component: vx,ball=v0cosθ
- Vertical component: vy,ball=v0sinθ
2. Determine the Horizontal Motion of the Person:
The person starts running with a constant speed of v02. The horizontal displacement of the person after time T is:
xperson=(v02)T
3. Calculate the Horizontal Displacement of the Ball:
The horizontal displacement of the ball after time T is:
xball=(v0cosθ)T
4. Set the Horizontal Displacements Equal:
For the person to catch the ball, their horizontal displacements must be equal at time T:
xperson=xball
Substituting the expressions we derived:
(v02)T=(v0cosθ)T
5. Simplify the Equation:
We can cancel T from both sides (assuming T≠0):
v02=v0cosθ
Dividing both sides by v0 (assuming v0≠0):
12=cosθ
6. Find the Angle θ:
To find θ, we take the inverse cosine:
θ=cos−1(12)
This gives us:
θ=60∘
Conclusion:
Yes, the person will be able to catch the ball if the angle of projection θ is 60∘.
---
The ball is thrown with an initial speed v0 at an angle θ. The horizontal and vertical components of the ball's velocity can be expressed as:
- Horizontal component: vx,ball=v0cosθ
- Vertical component: vy,ball=v0sinθ
The person starts running with a constant speed of v02. The horizontal displacement of the person after time T is:
xperson=(v02)T
The horizontal displacement of the ball after time T is:
xball=(v0cosθ)T
For the person to catch the ball, their horizontal displacements must be equal at time T:
xperson=xball
Substituting the expressions we derived:
(v02)T=(v0cosθ)T
We can cancel T from both sides (assuming T≠0):
v02=v0cosθ
Dividing both sides by v0 (assuming v0≠0):
12=cosθ
To find θ, we take the inverse cosine:
θ=cos−1(12)
This gives us:
θ=60∘
Yes, the person will be able to catch the ball if the angle of projection θ is 60∘.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct11videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Assertion - Reasoning5videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Subjective40videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
Similar Questions
A boy throws a ball with a velocity u at an angle θ with the horizontal. At the same instant he starts running with uniform velocity to catch the ball before it hits the ground. To achieve this he should run with a velocity of
View SolutionA ball is fired from point P, with an initial speed of 50ms−1 at an angle of 53∘, with the horizontal. At the same time, a long wall ABat200m from point P starts moving toward P with a constant speed of 10ms−1. Find
(a) the time when the ball collides with wall AB.
(b) the coordinate of point C, where the ball xollides, taking point P as origin.
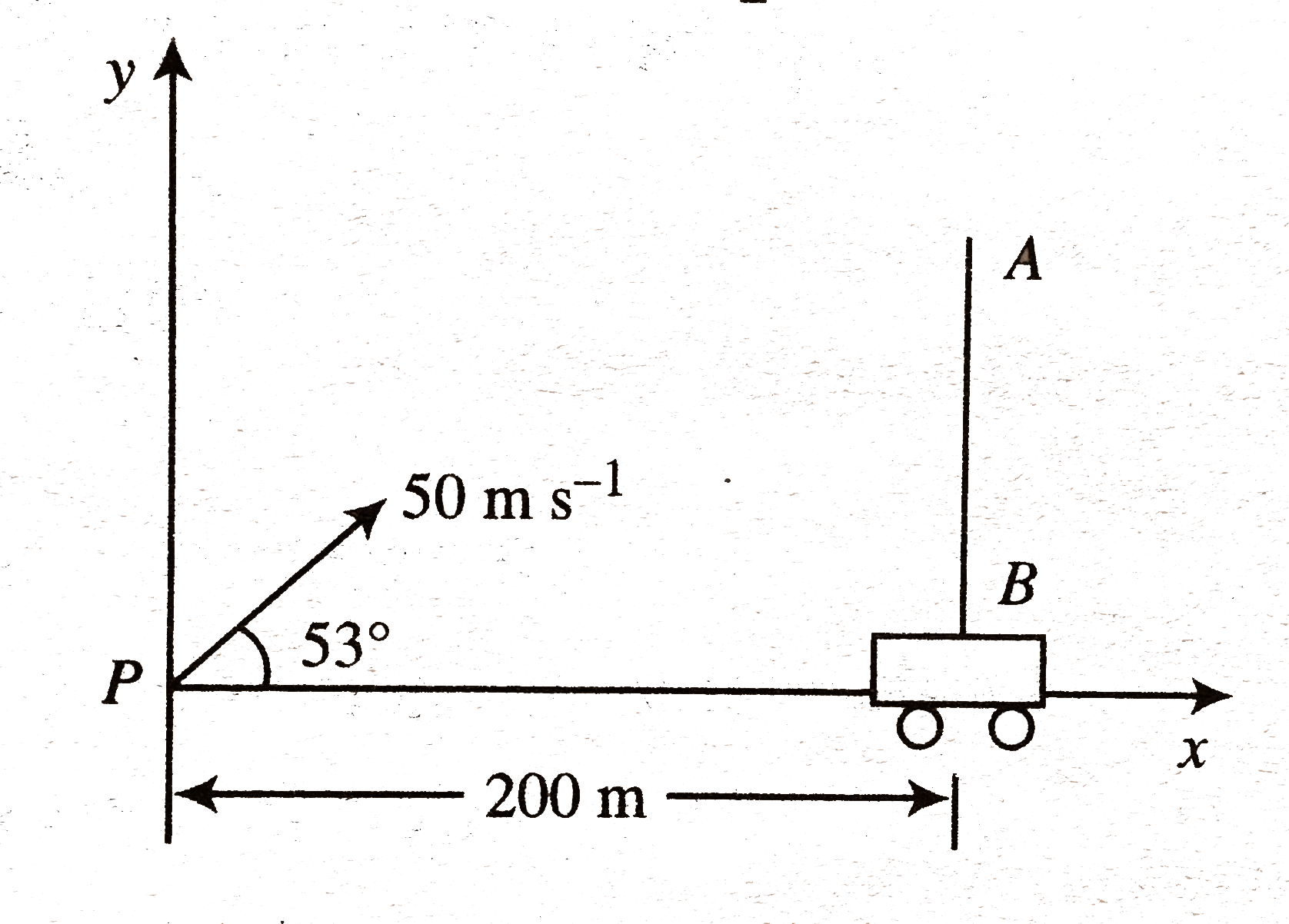 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One
A ball A is thrown up vertically with a speed u and at the same instant another ball B is released from a height h. At time t, the speed A relative to B is
AuBu - 2gtC√u2−2ghDu - gt
A ball is thrown onto a smooth floor with speed u at angle θ=45∘. If it rebounds with a speed v at the same angle ϕ=45∘. Then the coefficient of restitution is
 View Solution
View SolutionA ball is projected from top of the table with initial speed u at an angle of inclination θ, motion of image of ball w.r.t ball
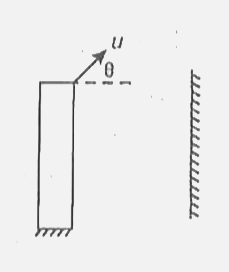 View Solution
View SolutionA ball is thrown downward In a viscous fluid with speed V. Terminal speed of ball is V0
 View Solution
View SolutionA projectile thrown with a speed v at an angle θ has a range R on the surface of earth. For same v and θ, its range on the surface of moon will be
View SolutionA ball is thrown horizontally from a point O with speed 20 m/s as shown. Ball strikes the incline along normal after two seconds
The speed of ball just before striking the plane is:
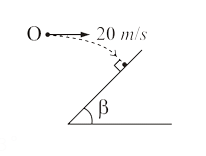 View Solution
View SolutionA projectile is thrown with a speed v at an angle θ with the vertical. Its average velocity between the instants it crosses half the maximum height is
View SolutionA foot ball is kicked of with an inirial speed of 19.6 m/sec at a projection angle 45∘ . A receiver on the goal line 67.4 m away in the direction of the kick starts running to meet the ball at that in stant. What must his speed be if he is to catch the ball before it hits the ground?
View Solution

