Two paper screens A and B are separated by 150m. A bullet pierces A and B. The hole in B in 15 cm below the hole in A. If the bullet is travelling horizontally at the time of hitting A, then the velocity of the bullet at A is: (g=10ms−2)
100√3ms−1
200√3ms−1
300√3ms−1
500√3ms−1
The correct Answer is:D
To solve the problem step by step, we will analyze the motion of the bullet as it travels horizontally and vertically between the two screens A and B.
Step 1: Understand the scenario
The bullet travels horizontally and pierces through two screens A and B, which are separated by a vertical distance of 15 cm (or 0.15 m) and a horizontal distance of 150 m.
Step 2: Calculate the time of flight
Since the bullet is traveling horizontally, we can use the equations of motion to find the time it takes for the bullet to fall 0.15 m vertically due to gravity. The vertical motion can be described by the equation:
h=12gt2
Where:
- h=0.15m (the vertical distance fallen)
- g=10m/s2 (acceleration due to gravity)
- t is the time of flight.
Rearranging the equation to solve for t:
t2=2hg
Substituting the values:
t2=2×0.1510=0.310=0.03
Taking the square root:
t=√0.03=√3×10−2=√3/10s
Step 3: Calculate the horizontal velocity
The horizontal distance traveled by the bullet is 150 m. The horizontal velocity u can be calculated using the formula:
u=distancetime=150t
Substituting t:
u=150√3/10=150×10√3=1500√3m/s
Step 4: Simplify the expression
To express the velocity in a more standard form, we can multiply the numerator and the denominator by √3:
u=1500√33=500√3m/s
Final Answer
Thus, the velocity of the bullet at screen A is:
u=500√3m/s
The bullet travels horizontally and pierces through two screens A and B, which are separated by a vertical distance of 15 cm (or 0.15 m) and a horizontal distance of 150 m.
Since the bullet is traveling horizontally, we can use the equations of motion to find the time it takes for the bullet to fall 0.15 m vertically due to gravity. The vertical motion can be described by the equation:
- h=0.15m (the vertical distance fallen)
- g=10m/s2 (acceleration due to gravity)
- t is the time of flight.
The horizontal distance traveled by the bullet is 150 m. The horizontal velocity u can be calculated using the formula:
To express the velocity in a more standard form, we can multiply the numerator and the denominator by √3:
Thus, the velocity of the bullet at screen A is:
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct11videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Assertion - Reasoning5videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Subjective40videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
Similar Questions
Two paper screens A and B are separated by a distance of 100m. A bullet pierces A and B. The hole in B is 10cm below the hole in A. If the bullet is travelling horizontally at the time of hitting the screen A, calculate the velocity of the bullet when it hits the screen A. Neglect resistance of paper and air.
View SolutionA bullet fired vertically up from the ground reaches a point in its path after 3s and 13 s, both times being taken from the instant of firing the bullet. The velocity of projection of the bullet is (g=10ms−2)
View SolutionA bullet is projected upwards from the top of a tower of height 90 m with the velocity 30ms−1 making an angle 30∘ with the horizontal. Find the time taken by it to reach the ground is (g=10ms−2)
View SolutionTwo thin wood screens A and B are separated by 200m. A bullet travelling horizontally at a speed of 600ms−1 hits the screen A, penetrates through it and finally emerges out from B making holes in A and B. If the resistance of air and wood arc negligible, the difference of heights of the holes in A and B is
View SolutionPoints A and C are on the horizontal ground and A and B are in same vertical plane at a distance of 1500m. Simultaneously bullets are fired from A,Bll and C and they collide at O. The bullets at B is fired at an angle of 30∘with horizontal towards the ground iat velocity 100m/s. the bullet at C is projected vertically upwards at velocity of 100m/s. the bullet projected from A reaches its maximum height at O.
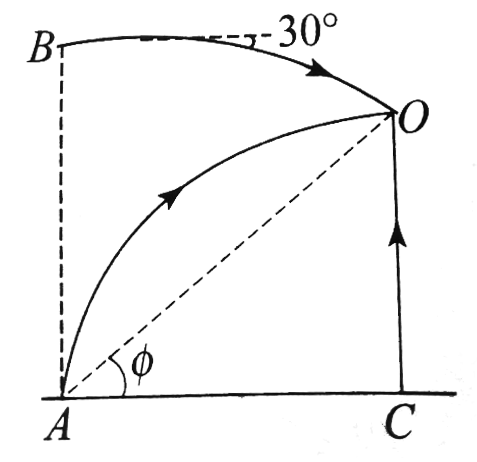
Find the time in which bullets will collide (seconds ):View SolutionPoints A and C are on the horizontal ground and A and B are in same vertical plane at a distance of 1500m. Simultaneously bullets are fired from A,Bll and C and they collide at O. The bullets at B is fired at an angle of 30∘with horizontal towards the ground iat velocity 100m/s. the bullet at C is projected vertically upwards at velocity of 100m/s. the bullet projected from A reaches its maximum height at O.
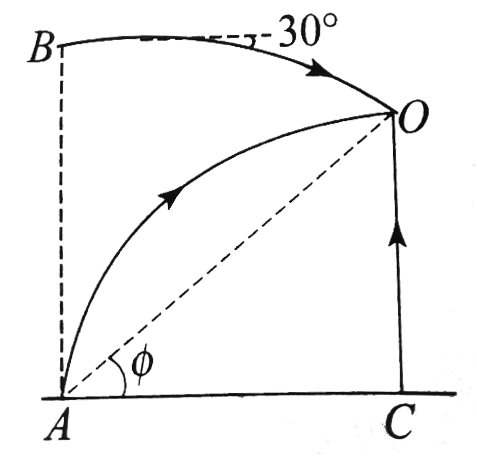
Find the velocity of bullet at A:View SolutionPoints A and C are on the horizontal ground and A and B are in same vertical plane at a distance of 1500m. Simultaneously bullets are fired from A,Bll and C and they collide at O. The bullets at B is fired at an angle of 30∘with horizontal towards the ground iat velocity 100m/s. the bullet at C is projected vertically upwards at velocity of 100m/s. the bullet projected from A reaches its maximum height at O.
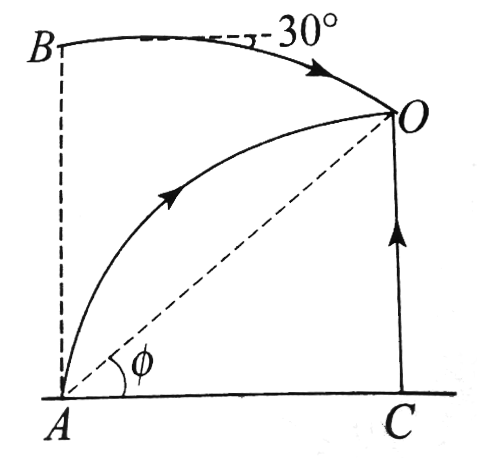
Find the elevation angle ∠θ=∠OAC:View SolutionIn the given figure points A and C are on the horizontal ground & A and B are in same vertical plane. Simultaneously bullets are fired from A, B and C and they collide at D. The bullet at B is fired horizontally with speed of 725km/hr and the bullet at C is projected vertically upward at velocity of 545km/hr. Find velocity of the bullet projected from A in m/s.
 View Solution
View SolutionThe level of water in a tank is 5 m high. A hole of area of cross section 1 cm2 is made at the bottom of the tank. The rate of leakage of water for the hole in m3s−1 is (g=10ms−2)
View SolutionAn open vessel containing the liquid upto a height of 15 m. A small hole is made at height of 10 m from the base of the vessel then the initial velocity of efflux is (g = 10 m/s2)
View Solution

