Suppose two particles 1and2 are projected in vertical plane simultaneously.
Their angles of projection are 30∘andθ, respectively, with the horizontal. Let they collide after a timet in air. Then
 .
.
θ=sin−1(4/5) and they will have same speed just before the collision.
θ=sin−1(4/5) and they will have different speed just before the collision.
x<1280√3−960m.
It is possible that the particles collide when both of them are at their highest point.
The correct Answer is:C, D
(b.,c.,d.) If they collide, their vertical component of velocities should be same, i.e.,
100sinθ=160sin30∘
⇒sinθ=4/5
Their vertical components will always be same. Horizontal components :
160cos30=80√3ms−1
and 100cosθ=100×3/5=60ms−1
They are not same, hence their velocities will not be same at any time. So (b) is correct.
x=x1−x2=160cos30∘t−100cosθt
⇒x=(80√3−60)t
Time of flight : T=2×160×sin30g=16s (same for both)
Now t<Tx→ to collide in air
⇒x80√3−60<16⇒x<1280√3−960
Since their times of flight are same, they will simultaneously reach their maximum height. So it is possible to collide at the highest point for certain values of x.
 .
.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Assertion - Reasoning
5 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Comprehension
21 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Single Correct
76 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
Two particles are projected simultaneously in the same vertical plane, with speed u1 and u2 at angle of projection θ1 and θ2 respectively with the horizontal. The path followed by one, as seen by other (as long as both are in flight), is
View SolutionTwo particles are projected with same velocity but at angles of projection 25° and 65° with horizontal. The ratio of their horizontal ranges is
View SolutionTwo particles are projected simultaneously with same speed V0 in same vertical plane at angle 30∘and60∘ With the horizontal .The time at which their velocities becomes parallel is
View SolutionTwo particles P & Q are projected simultaneously from a point O on a level ground in the same vertical plane with the same speed in directions making angle of 30∘ and 60∘ respectively with the horizontal.
View SolutionFigure shows that particle A is projected from point P with velocity u along the plane and simultaneously another particle B with velocity v at an angle α with vertical. The particles collide at point Q on the plane. Then
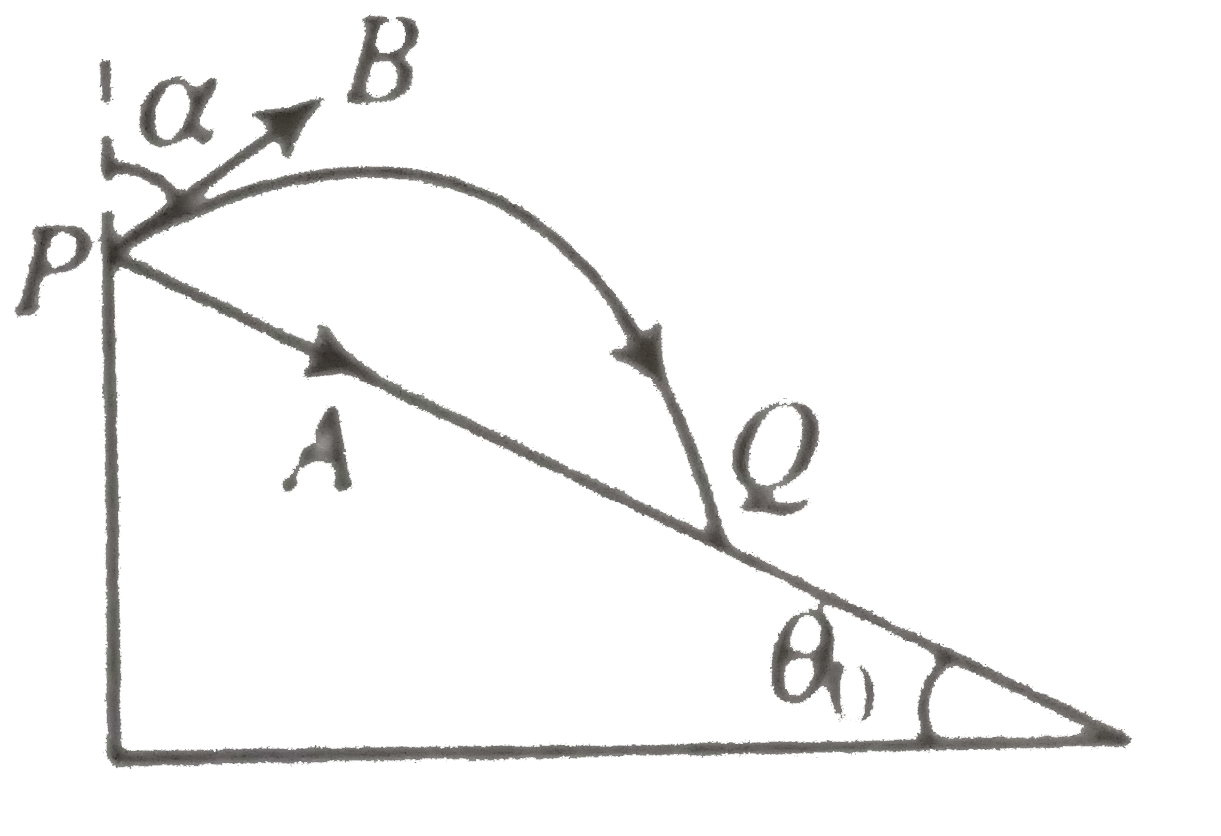
View SolutionTwo particles A and B are projected simultaneously from a fixed point of the ground. Particle A is projected on a smooth horizontal surface with speed v, while particle B is projected in air with speed v, while particle B is projected in air with speed 2v√3. If particle B hits the particle A, the angle of projection of B with the vertical is
View SolutionA particle is projected with a speed u. If after 2 seconds of projection it is found to be making an angle of 45∘ with the horizontal and 0∘ after 3 sec, then:
View SolutionTwo identical balls P and Q are projected with same speeds in a vertical plane from the same point O making projection angles with horizontal 30∘ and 60∘, respectively and they fall directly on the plane AB at points P' and Q' respectively. Which of the following statement is true about distances as given in options ?
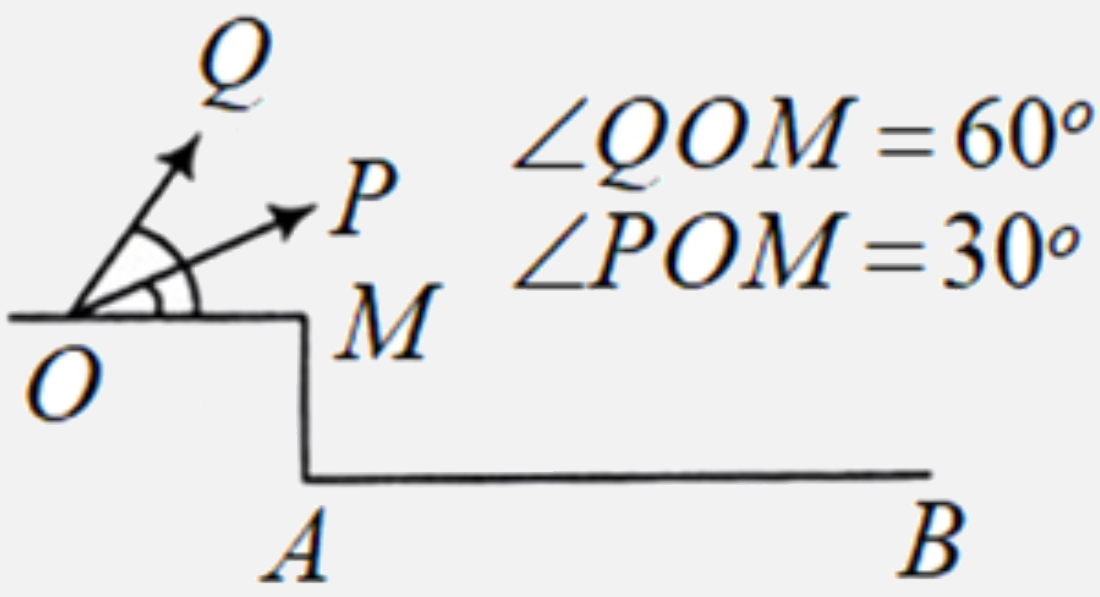
View SolutionTwo particles A and B are projected simultaneously in a vertical plane as shown in figure. They collide at time t in air. Write down two necessary equations for collision to take place.

View SolutionTwo particles are simultaneously projected in the same vertical plane from the same point with velocities u and v at angles αandβ with horizontal. Find the time that elapses when their velocities are parallel.
View Solution
