Two particles A and B are projected simultaneously from a fixed point of the ground. Particle A is projected on a smooth horizontal surface with speed v, while particle B is projected in air with speed v, while particle B is projected in air with speed 2v√3. If particle B hits the particle A, the angle of projection of B with the vertical is
30∘
60∘
Both (a) and (b)
45∘
The correct Answer is:A
To solve the problem, we need to determine the angle of projection of particle B with respect to the vertical when it hits particle A. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the motion of both particles
- Particle A is projected horizontally with speed v.
- Particle B is projected at an angle θ with speed 2v√3.
Step 2: Set up the equations for horizontal displacement
- The horizontal displacement of particle A after time t is given by:
xA=vt
- The horizontal displacement of particle B is given by:
xB=(2v√3cosθ)t
Step 3: Set the horizontal displacements equal to each other
Since both particles hit each other at the same horizontal position, we can equate their displacements:
vt=(2v√3cosθ)t
Step 4: Simplify the equation
We can cancel t from both sides (assuming t≠0):
v=2v√3cosθ
Dividing both sides by v (assuming v≠0):
1=2√3cosθ
Step 5: Solve for cosθ
Rearranging gives:
cosθ=√32
Step 6: Find the angle θ
The angle θ for which cosθ=√32 is:
θ=30∘
Step 7: Find the angle with respect to the vertical
Since the angle of projection is given with respect to the horizontal, to find the angle with respect to the vertical, we subtract θ from 90∘:
Angle with vertical=90∘−30∘=60∘
Final Answer
The angle of projection of particle B with the vertical is 60∘.
---
- Particle A is projected horizontally with speed v.
- Particle B is projected at an angle θ with speed 2v√3.
- The horizontal displacement of particle A after time t is given by:
xA=vt
- The horizontal displacement of particle B is given by:
xB=(2v√3cosθ)t
Since both particles hit each other at the same horizontal position, we can equate their displacements:
vt=(2v√3cosθ)t
We can cancel t from both sides (assuming t≠0):
v=2v√3cosθ
Dividing both sides by v (assuming v≠0):
1=2√3cosθ
Rearranging gives:
cosθ=√32
The angle θ for which cosθ=√32 is:
θ=30∘
Since the angle of projection is given with respect to the horizontal, to find the angle with respect to the vertical, we subtract θ from 90∘:
Angle with vertical=90∘−30∘=60∘
The angle of projection of particle B with the vertical is 60∘.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - B. Medical entrance1videos
MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrance12videos
MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - A. Taking it together1videos
MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective19videos
MEASUREMENT AND ERRORS
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery32videos
MOTION IN A PLANE
Similar Questions
Two particles A and B are projected simultaneously from two towers of heights 10 m and 20m respectively. Particle A is projected with an initial speed of 10√2m/s at an angle of 45∘ with horizontal, while particle B is projected horizontally with speed 10m/s. If they collide in air, what is the distance d between the towers?
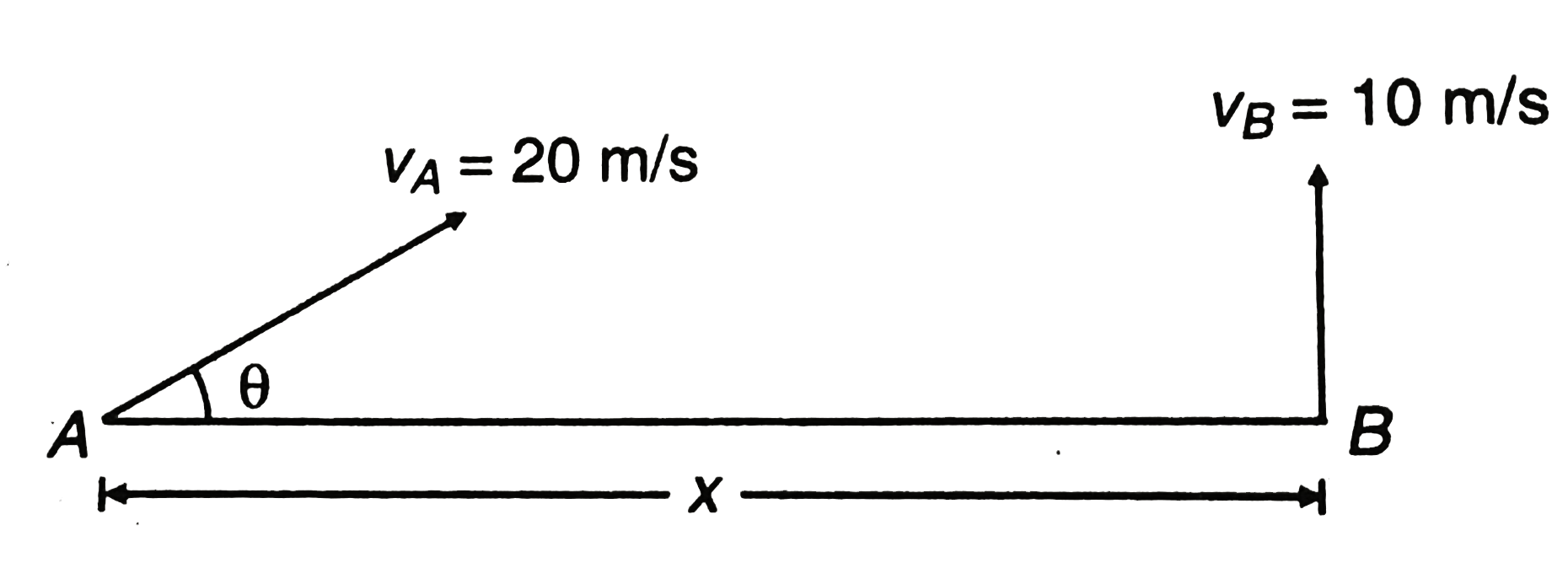 View Solution
View SolutionA particle is projected vertically upwards in vacuum with a speed u.
View SolutionA particle is projected in gravity with a speed v0. Using W-E theorem, find the speed of the particle as the function of vertical distance y.
View SolutionA particle is projected at an angle θ with an initial speed u.
View SolutionTwo particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then:
 View Solution
View SolutionTwo particles are projected simultaneously from two towers of different heights,one is horizontal with speed 10 m/s and the other at an angle 45° below the horizontal with speed v as shown in figure. The velocity v for which particles collides in air is
 View Solution
View SolutionIf a charged particle is projected on a rough horizontal surface with speed v0. Find the value of dynamic coefficient of friction, if the kinetic energy of system is constant.
 View Solution
View SolutionTwo particles A and B are placed as shown in figure. The particle A, on the top of tower, is projected horizontally with a velocity u and particle B is projected along the surface towards the tower, simultaneously. If both particles meet each other, then the speed of projection of particles B is [ignore any friction]
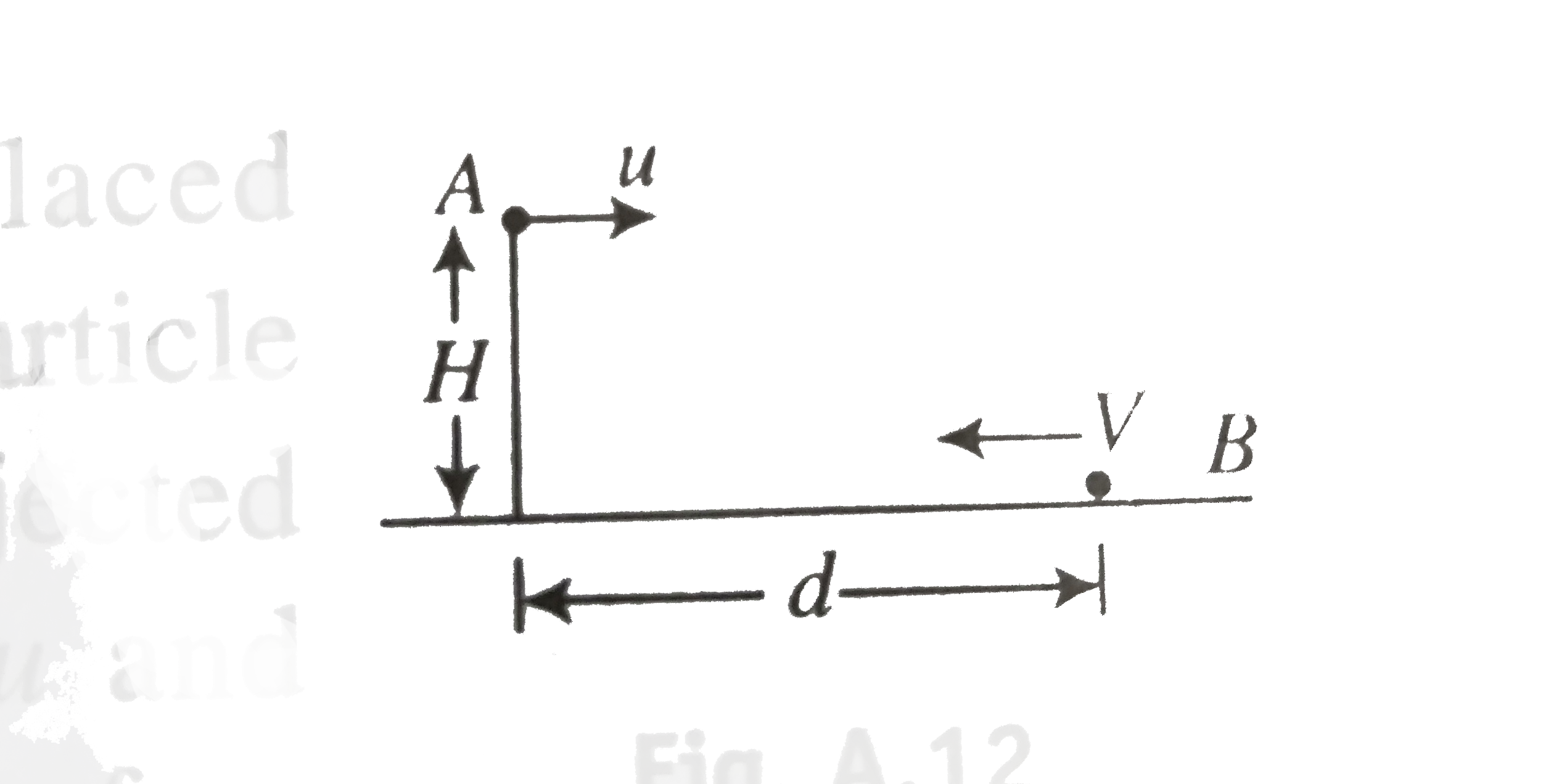 View Solution
View SolutionA particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View Solution

