What is the radius of curvature of the parabola traced out by the projectile in the previous problem projected with speed v at an angle of theta with the horizontal at a point where the particle velocity makes an angle θ2 with the horizontal?
u2cos2sec3(θ2)g
u2cos2sec3(θ2)2g
2u2cos2θsec3(θ2)g
u2cos2θsec3(θ2)√3g
The correct Answer is:A
(a) We know that ac=v2r⇒r=v2ac, where r is known as radius of curvature. At the highest point, v=ucosθ,
ac=g⇒r=u2cos2θg
Similarly, find the velocity and ac at the given point and then find r.ac will be component of g perpendicular to velocity at that point (Fig. S5.93).
vcos(θ/2)=ucosθ
⇒v=ucosθsec(θ/2)
ac=gcos(θ/2)
Now find r=v2ac
h=H/2,vcosϕ=ucosθ ...(i)
v2sin2ϕ=u2sin2θ−2g(H)2...(ii)
Squaring Eq. (i) and adding in Eq. (ii), we get
v2=u2−gH where H=u2sinθ2g
ac=gcosϕ=gucosθv
Now r=v2ac.
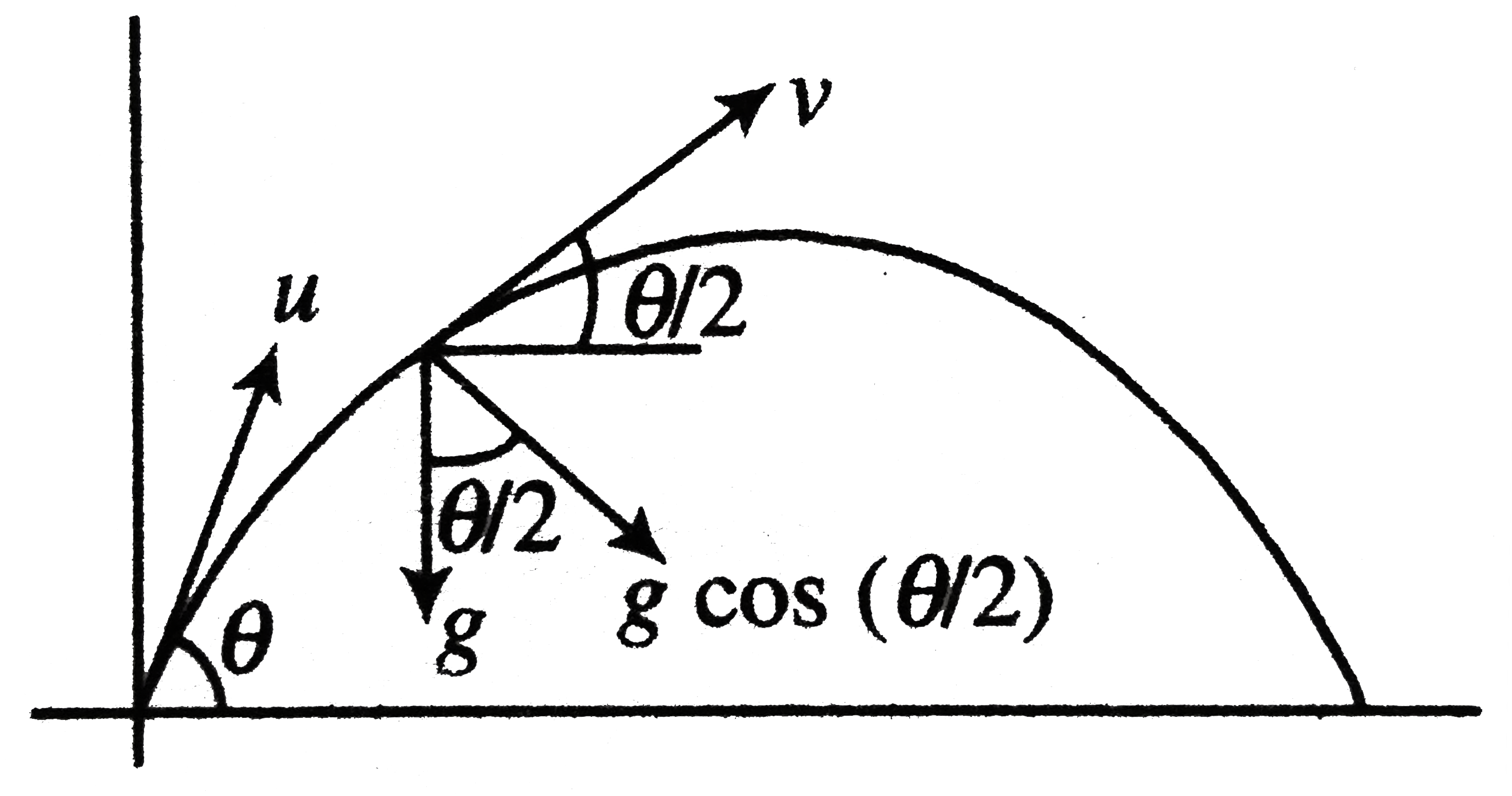 ,
,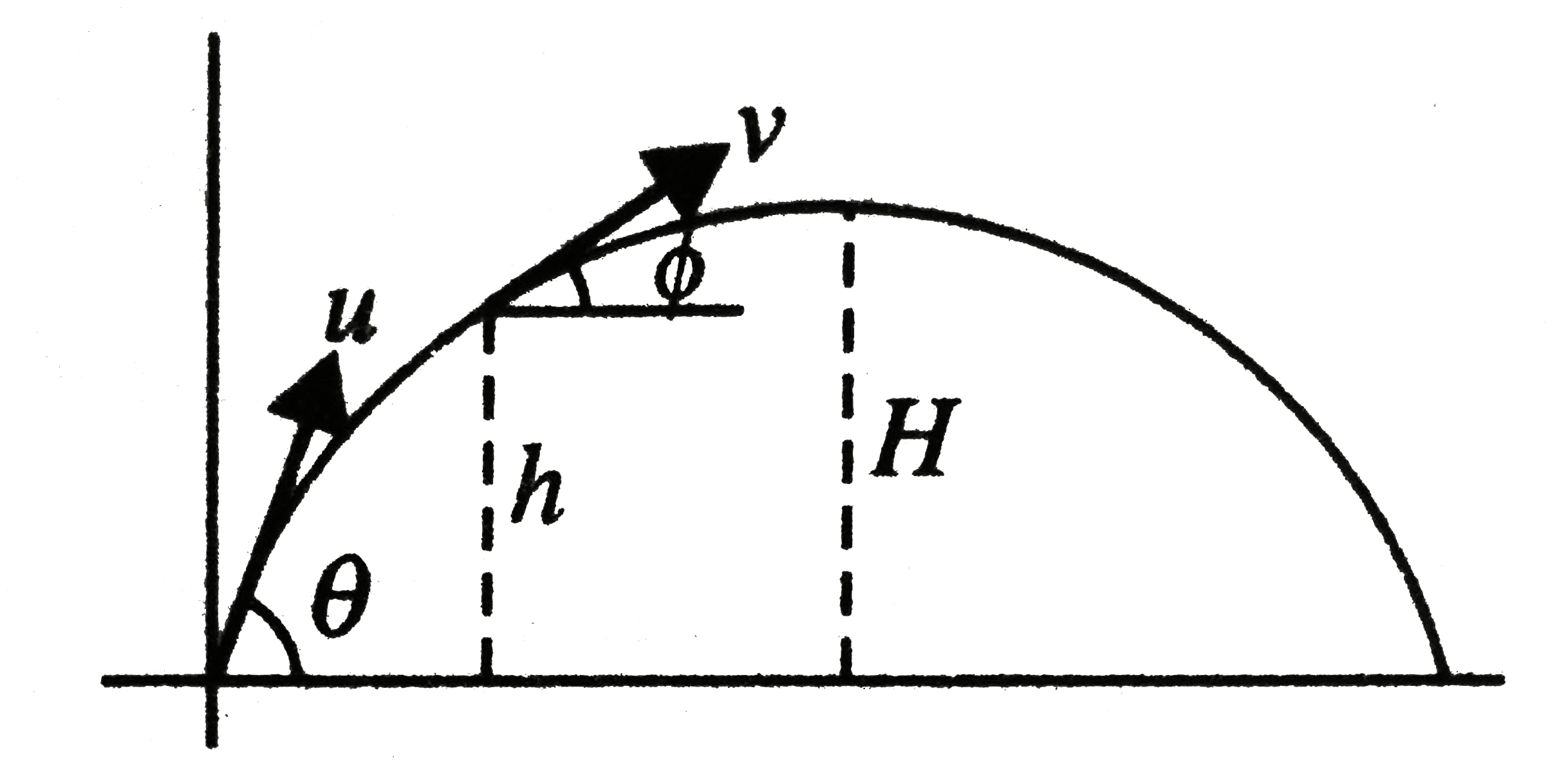 .
.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer9videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Assertion - Reasoning5videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
Similar Questions
What is the radius of curvature of the parabola traced out by the projectile in which a particle is projected by a speed u at an angle 'theta' with the horizontal, at a point where the particle velocity makes and angle θ2 with the horizontal?
View SolutionWhat is the radius of curvature of the parabola traced out by the projectile in which a particle is projected with a speed u at an angle θ with the horizontal, at a point where the velocity of particle makes an angle θ/2 with the horizontal.
View Solution
Knowledge Check
- Question 1 - Select One
If a body is projected with an angle θ to the horizontal, then
Aits velocity is always perpendicular to its acceleration thenBits velocity becomes zero at its maximum height.Cits velocity makes zero angle with the horizontal at its maximum height.Dthe body just before hitting the ground, the direction of velocity coincides with the acceleration. - Question 2 - Select One
A particle is thrown with a speed is at an angle θ with the horizontal. When the particle makes an angle ϕ with the horizontal, its speed changes to v, then
Av=v0cosθBv=v0cosθ⋅cosϕCv=v0cosθ⋅secϕDv=v0secθ⋅cosϕ
A projectile is fired with a speed u at an angle θ with the horizontal. Find its speed when its direcrtion of motion makes an angle α with the horizontal.
View SolutionA projectile is fired with a speed u at an angle θ with the horizontal. Find its speed when its direction of motion makes an angle α with the horizontal.
View SolutionA particle is thrown with a speed u at an angle θ with the horizontal. When the particle makes an angle ϕ with the horizontal. Its speed changes to v :
View SolutionA particle is fired from a point on the ground with speed u making an angle θ with the horizontal.Then
View SolutionA particle is projected with velocity 50 m/s at an angle 60∘ with the horizontal from the ground. The time after which its velocity will make an angle 45∘ with the horizontal is
View SolutionA projectile is projected with speed u at an angle θ with the horizontal . The average velocity of the projectile between the instants it crosses the same level is
View Solution

