From a tower of height 40m, two bodies are simultaneously projected horizontally in opposite direction, with velocities 2ms−1and8ms−1. respectively.
The horizontal distance between two bodies, when their velocity are perpendicular to each other, is.
1 m
0.5 m
2 m
4 m
The correct Answer is:D
To solve the problem, we need to find the horizontal distance between two bodies projected horizontally from a height of 40 m when their velocities become perpendicular to each other. Let's break it down step by step.
Step 1: Identify the initial conditions
- Height of the tower (h) = 40 m
- Velocity of body A (v_A) = 2 m/s (to the left)
- Velocity of body B (v_B) = 8 m/s (to the right)
Step 2: Determine the vertical motion
Since both bodies are projected horizontally, their initial vertical velocities are zero. The vertical motion of both bodies is influenced by gravity. The vertical velocity (v_y) at any time (t) can be calculated using the formula:
vy=g⋅t
where g is the acceleration due to gravity (approximately 10m/s2).
Step 3: Calculate the time taken to fall 40 m
Using the equation of motion for vertical displacement:
h=12gt2
we can rearrange this to find the time t it takes for the bodies to fall 40 m:
40=12⋅10⋅t2
40=5t2
t2=405=8
t=√8=2√2s
Step 4: Write the expressions for the velocities
The velocities of the two bodies at time t can be expressed as:
- Velocity of body A:
→vA=−2^i−gt^j
- Velocity of body B:
→vB=8^i−gt^j
Step 5: Determine when the velocities are perpendicular
The velocities are perpendicular when their dot product is zero:
→vA⋅→vB=0
Calculating the dot product:
(−2^i−gt^j)⋅(8^i−gt^j)=−16+g2t2=0
This simplifies to:
g2t2=16
Substituting g=10:
100t2=16
t2=16100=0.16
t=0.4s
Step 6: Calculate the horizontal distance
Now, we can calculate the horizontal distance traveled by both bodies in this time:
- Distance traveled by body A:
dA=vA⋅t=2⋅0.4=0.8m
- Distance traveled by body B:
dB=vB⋅t=8⋅0.4=3.2m
Step 7: Find the total horizontal distance between the two bodies
The total horizontal distance between the two bodies when their velocities are perpendicular is:
dtotal=dA+dB=0.8+3.2=4m
Final Answer
The horizontal distance between the two bodies when their velocities are perpendicular to each other is 4 meters.
---
- Height of the tower (h) = 40 m
- Velocity of body A (v_A) = 2 m/s (to the left)
- Velocity of body B (v_B) = 8 m/s (to the right)
Since both bodies are projected horizontally, their initial vertical velocities are zero. The vertical motion of both bodies is influenced by gravity. The vertical velocity (v_y) at any time (t) can be calculated using the formula:
vy=g⋅t
where g is the acceleration due to gravity (approximately 10m/s2).
Using the equation of motion for vertical displacement:
h=12gt2
we can rearrange this to find the time t it takes for the bodies to fall 40 m:
40=12⋅10⋅t2
40=5t2
t2=405=8
t=√8=2√2s
The velocities of the two bodies at time t can be expressed as:
- Velocity of body A:
→vA=−2^i−gt^j
- Velocity of body B:
→vB=8^i−gt^j
The velocities are perpendicular when their dot product is zero:
→vA⋅→vB=0
Calculating the dot product:
(−2^i−gt^j)⋅(8^i−gt^j)=−16+g2t2=0
This simplifies to:
g2t2=16
Substituting g=10:
100t2=16
t2=16100=0.16
t=0.4s
Now, we can calculate the horizontal distance traveled by both bodies in this time:
- Distance traveled by body A:
dA=vA⋅t=2⋅0.4=0.8m
- Distance traveled by body B:
dB=vB⋅t=8⋅0.4=3.2m
The total horizontal distance between the two bodies when their velocities are perpendicular is:
dtotal=dA+dB=0.8+3.2=4m
The horizontal distance between the two bodies when their velocities are perpendicular to each other is 4 meters.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Assertion - Reasoning
5 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
From a tower of height 40m, two bodies are simultaneously projected horizontally in opposite direction, with velocities 2ms−1and8ms−1. respectively.
The time taken for the displacement vectors of two bodies to be come perpendicular to each other is.
View SolutionFrom a tower of height 40m, two bodies are simultaneously projected horizontally in opposite direction, with velocities 2ms−1and8ms−1. respectively.
The time taken for the velocity vectors of two bodies to become perpendicular to each other is :
View SolutionTwo particles are thrown horizontally in opposite directions from the same point from a height h with velocities 4ms−1and3ms−1 . What is the separation between them when their velocities are perpendicular to each other?
View SolutionTwo particles are projected from a tower horizontally in opposite directions with velocities 10m/sand20m/s. Find the time when their velocity vectors are mutually perpendicular. Take g=10m/s2.
View SolutionTwo particles are projected with speeds u1 and u2 in mutually opposite directions from top of a tower horizontally. Find the time after which their velocity becomes perpendicular to each other.
View SolutionTwo particles are located on a horizontal plane at a distance 60m. At t=0 both the particles are simultaneously projected at angle 45∘ with velocities 2ms−1and14ms−1, respectively. Find
(a) Minimum separation between them during motion.
(b) At what time is the separation between them minimum ?
 .
.
View SolutionTwo bodies are thrown simultaneously from a tower with same initial velocity v0: one vertically upwards, the other vertically downwards. The distance between the two bodies after time t is
View SolutionTwo bodies of same mass are projected with the same velocity at an angle 30∘ and 60∘ respectively.The ration of their horizontal ranges will be
View SolutionTwo stones are projected from the top of a tower in opposite directions, with the same velocity V but at 30∘ & 60∘ with horizontal respectively. The relative velocity of first stone relative to second stone is
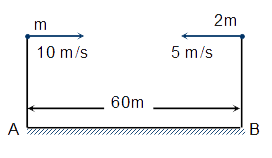
View SolutionTwo particles, one of mass m and the other of mass 2m, are projected horizontally towards each other from the same level above the ground with velocities 10 m/s and 5 m/s, respectively. They collide in air and stick to each other. The distance of the combined mass from point A is
View Solution
