You are designing an elevator for a hospital. The force exerted on a passenger by the floor of the elevator is not to exceed 1.60 times the passenger's weight. The elevator accelerates upwards with constant accelerates upwards with constant acceleration for a distance of 3.0 m and then starts to slow down. What is the maximum speed (in ) of the elevator?
The correct Answer is:6
To solve the problem step by step, we will follow these steps:
Step 1: Understand the forces acting on the passenger
The forces acting on the passenger in the elevator are:
- The weight of the passenger acting downwards, which is W=mg (where m is the mass of the passenger and g is the acceleration due to gravity).
- The normal force N exerted by the floor of the elevator acting upwards.
Step 2: Set up the inequality for the normal force
According to the problem, the normal force N should not exceed 1.6 times the weight of the passenger:
N≤1.6mg
Step 3: Apply Newton's second law
When the elevator accelerates upwards, we can apply Newton's second law:
N−mg=ma
Where a is the acceleration of the elevator. Rearranging gives:
N=mg+ma
Substituting the inequality for N:
mg+ma≤1.6mg
Step 4: Solve for the maximum acceleration
Rearranging the inequality:
ma≤1.6mg−mg
ma≤0.6mg
Dividing both sides by m (assuming m≠0):
a≤0.6g
Step 5: Substitute the value of g
Using g≈9.8m/s2:
a≤0.6×9.8m/s2
a≤5.88m/s2
Step 6: Calculate the maximum speed after accelerating for 3 meters
Using the kinematic equation:
v2=u2+2as
Where:
- v is the final velocity,
- u is the initial velocity (which is 0 since the elevator starts from rest),
- a is the maximum acceleration (5.88m/s2),
- s is the distance (3m).
Substituting the values:
v2=0+2×5.88×3
v2=35.28
v=√35.28
v≈5.94m/s
Final Answer:
The maximum speed of the elevator is approximately 5.94m/s.
---
The forces acting on the passenger in the elevator are:
- The weight of the passenger acting downwards, which is W=mg (where m is the mass of the passenger and g is the acceleration due to gravity).
- The normal force N exerted by the floor of the elevator acting upwards.
According to the problem, the normal force N should not exceed 1.6 times the weight of the passenger:
N≤1.6mg
When the elevator accelerates upwards, we can apply Newton's second law:
N−mg=ma
Where a is the acceleration of the elevator. Rearranging gives:
N=mg+ma
Substituting the inequality for N:
mg+ma≤1.6mg
Rearranging the inequality:
ma≤1.6mg−mg
ma≤0.6mg
Dividing both sides by m (assuming m≠0):
a≤0.6g
Using g≈9.8m/s2:
a≤0.6×9.8m/s2
a≤5.88m/s2
Using the kinematic equation:
v2=u2+2as
Where:
- v is the final velocity,
- u is the initial velocity (which is 0 since the elevator starts from rest),
- a is the maximum acceleration (5.88m/s2),
- s is the distance (3m).
v2=0+2×5.88×3
v2=35.28
v=√35.28
v≈5.94m/s
The maximum speed of the elevator is approximately 5.94m/s.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Linked Comperhension46videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
Consider an elevator moving downwards with an acceleration a, the force exerted by a passenger of mass m on the floor of the elevator is :
View SolutionWhat normal force does the floor of an elevator exert on a 90 kg person if the person / elevator system accelerates upward at 1m/s2 ?
View SolutionAn elevator is moving vertically up with a acceleration a the force exerted on the floor by a passenger of mass m is
View SolutionA man of mass m is standing in an elevator moving downward with an acceleration g4. The force exerted by the bottom surface of the elevator on the man will be
View SolutionA spring of force constant 200Nm−1 has a block of mass 10 kg hanging at its one end and the other end of the spring is attached to the celling of an elevator. The elevator is rising upwards with an acceleration of g4 and the block is in equilibrium with respect to the elevator . when the acceleration of the elevator suddenly ceases , the block starts oscillating . What is the amplitude (in m) of these oscillations ?
View SolutionA man is standing on a weighing machine kept on the floor of an elevator. The ratio of measured weight of the man when elevator is at rest and when it is moving with downward acceleration a is 3 : 2. The value of a is :
View SolutionIf the elevator in shown figure is moving upwards with constant acceleration 1ms−2, tension in the string connected to block A of mass 6 kg would be ( take, g=10ms−2)
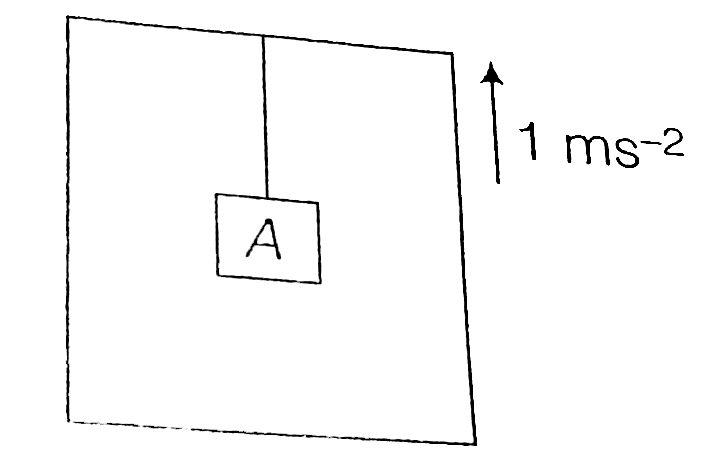 View Solution
View SolutionA cubical block of density ρ is floating on the surface of water. Out of its height L, fraction x is submerged in water. The vessel is in an elevator accelerating upward with acceleration a. What is the fraction immersed ?
View SolutionA spring mass system is hanging from the celling of an elevator in equilibrium. The elevator suddenly starts accelerating upwards with acceleration a. Find

(a) the frequency and
(b) the amplitude of the resulting SHM.View SolutionA block of mass m is suspended by a light thread from an elevator. The elevator is accelerating upward with uniform acceleration a. The work done by tension on the block during t seconds is (u = 0)
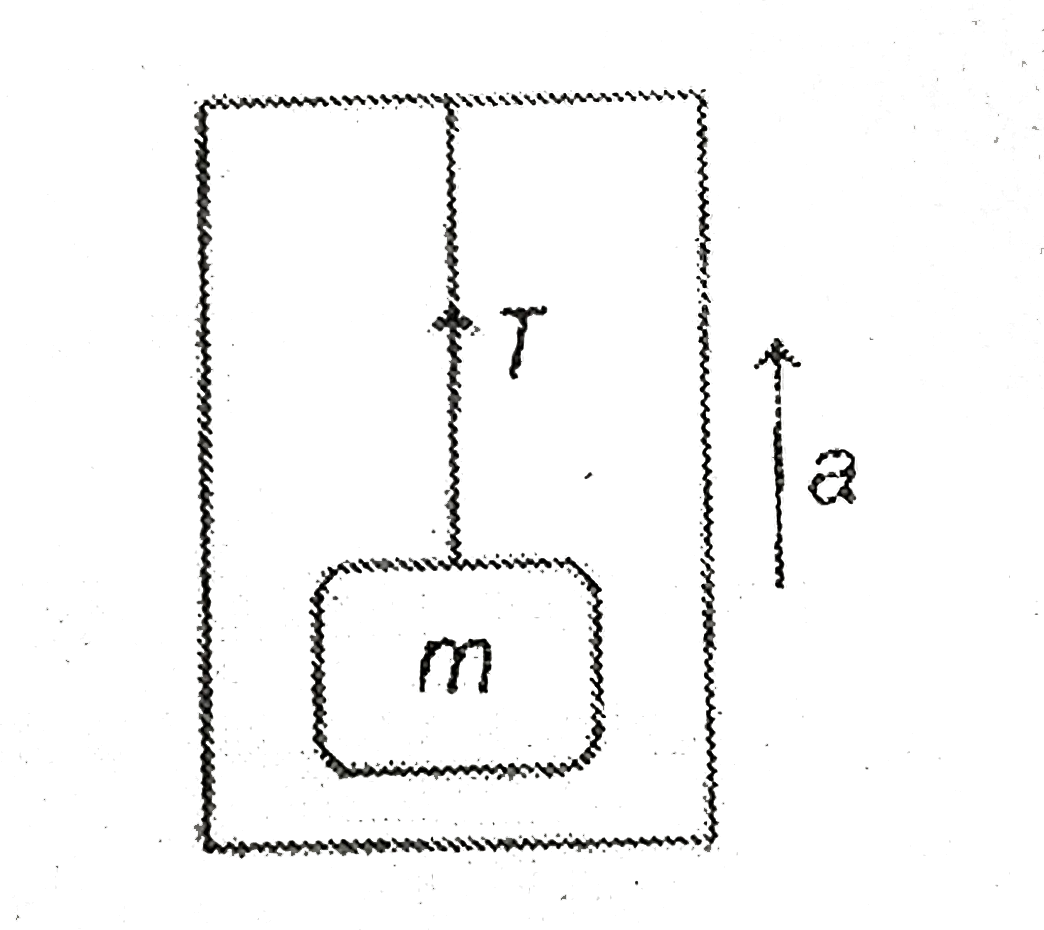 View Solution
View Solution

