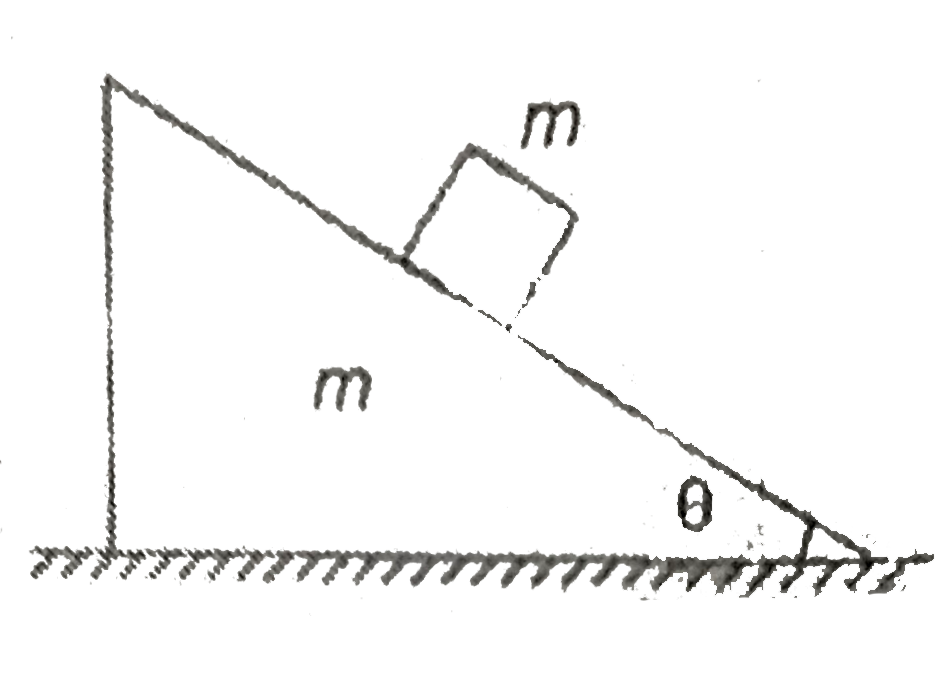
A block of mass as placed on a wedge of mass rest on a smooth flooras shpwn in Fig (a) . Friction exists between block and wedge.
a. Find the acceleration of each block if (i) and (ii)
b. Solve the problem if force is direction upwards as shown in Fig (b)

a. Assume that the system move together and friction between is static nature
Common acceleration
For block
For wedge
From (i) and (ii)
If friction is of static nature
For case (i) ,
Hence friction will be of static nature and will move with common acceleration
For case (ii)
The friction will be of kinetic nature both the block and the wedge will move with different acceleration .The friction between the block and wedges
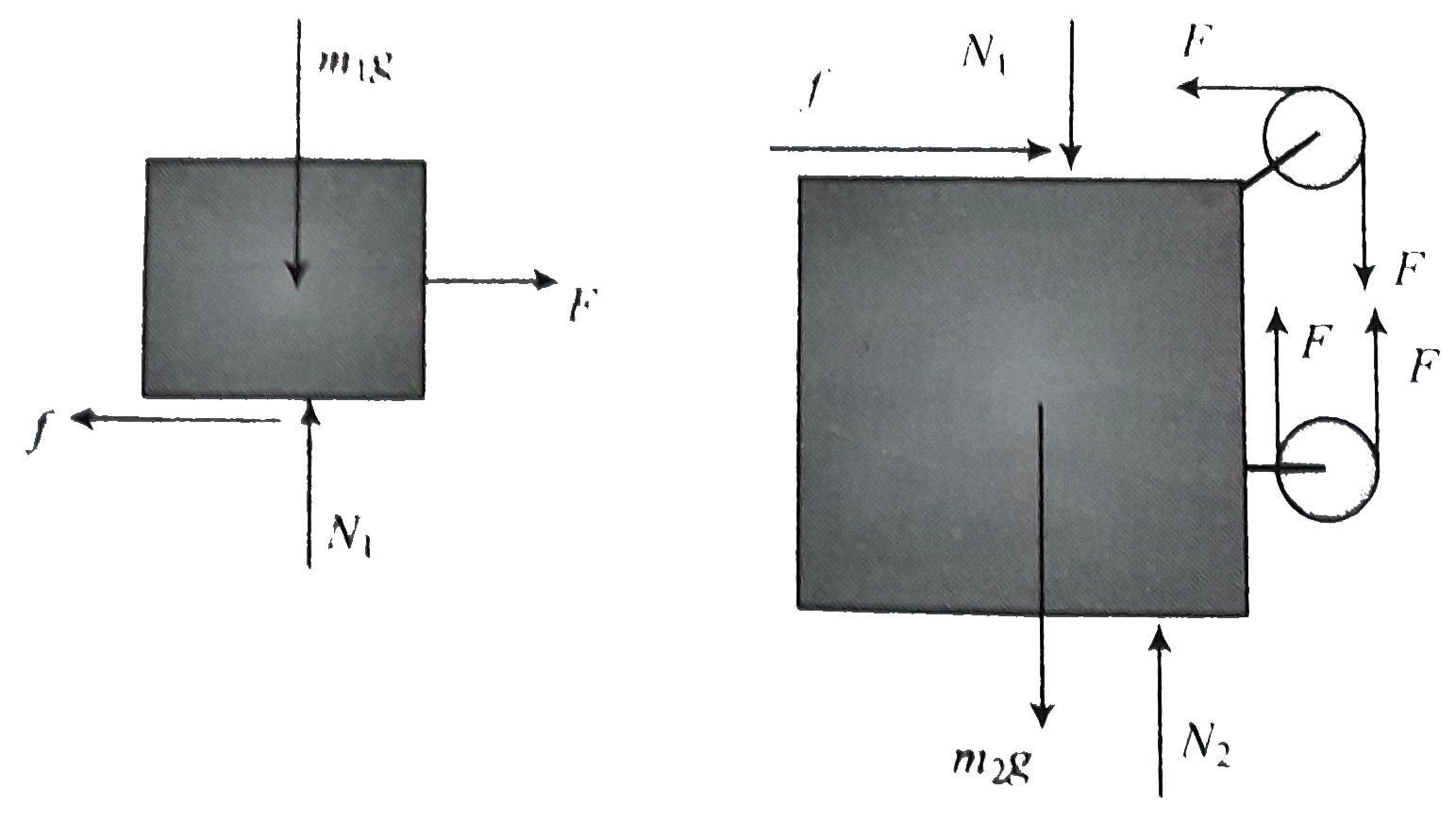
Acceleration of block,
Acceleration of wedge,
b. First we will determine the force for which block and wedge move in combination .From Newton's acceond law the equation are
Block
On solving the above equation simulaneously , we obtain
For no sliding
or
Here is greater than therefore occure New equation are
Block :
Wedge:
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.125videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.216videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
Two blocks of mass m and 2m are arranged on a wedge that is fixedd on a horizontal surface. Friction coefficient between the block and wedge are shown . Find the magnitude of acceleration of two blocks.
 View Solution
View SolutionBlock B rests on surface . If the coefficient of static friction between A and B is μ=0.4. Determine the acceleration of each , if
(a) F=30N and
(b) F=250N(g=10m/s2)
 View Solution
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released
 View Solution
View SolutionTwo block of masses m1andm2 are placed side by side on a smooth horizontal surface as shown in fig. A horizontal force F is applied on the block .

(a) Find the acceleration of each block.
(b) Find the normal reaction between the two blocks.View SolutionBlock B rests on a smooth surface .The coefficient of static friction between A and B is μ=0.4 where F=30N then

Acceleration of upper block isView SolutionA block of mass "5kg" is placed on a wedge having inclination of 37∘ with the horizontal. Coefficient of friction between block and wedge is 0.8. Then select the correct statement.
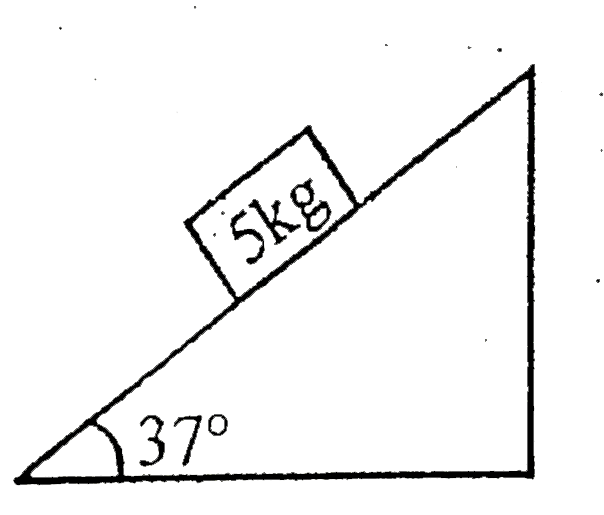 View Solution
View SolutionTwo block A and B are arrenged as shown in figure (mA=5kgandmB=10kg) Find the acceleration of blocks if F=40N
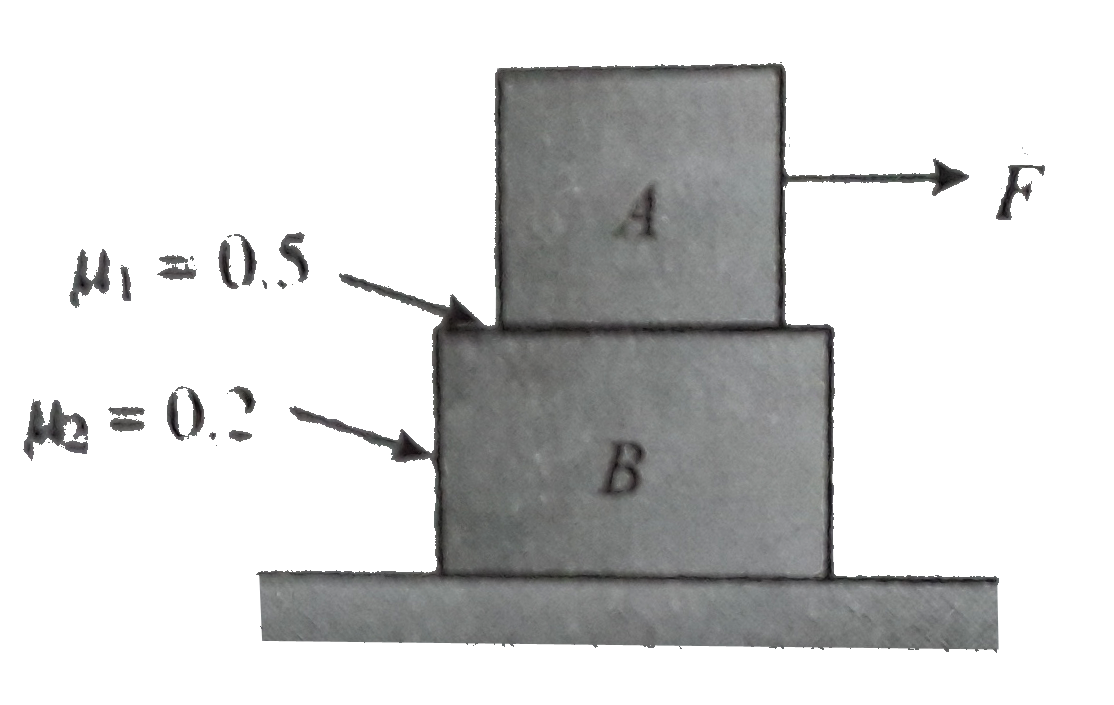 View Solution
View SolutionTwo blocks of masses 1 kg and 2 kg are placed in contact on a smooth horizontal surface as shown in fig. A horizontal force of 6N is applied d(a) on a 1-kg block. Find the force of interaction of the blocks.
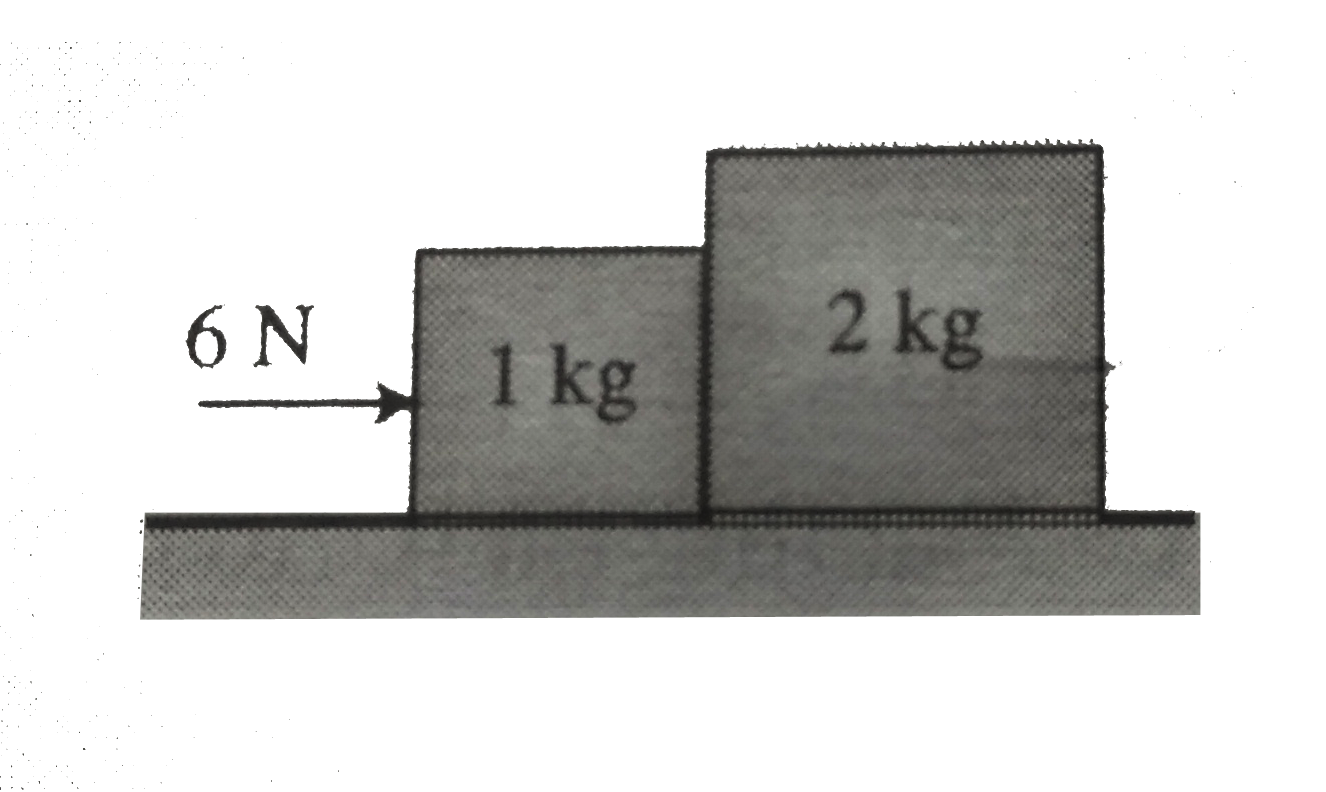
 .View Solution
.View SolutionA block mass m=2kg is accelerating by a force F=20N applied on a smooth light pully as shown in fig 7.86 If the coefficient of kinetic friction between the block and the surface is μ=0.3 find its acceleration
 View Solution
View SolutionA block of mass m slides down on inclined wedge of same mass m as shown in figure . Friction is absent everywhere . Acceleration of centre of mass of the block and wedge is
 View Solution
View Solution

