A bullet leaving the muzzle of a rifle barrel with a velocity v penetrates a plank and loses one-fifth of its velocity. It then strikes second plank, which it just penetrates through. Find the ratio of the thickness of the planks, supposing the average resistance to the penetration is same in both the cases.
To solve the problem, we need to find the ratio of the thickness of the two planks (let's denote them as S1 for the first plank and S2 for the second plank) based on the bullet's penetration and the loss of velocity.
1. Determine the initial velocity:
Let the initial velocity of the bullet as it leaves the rifle barrel be v=u.
2. Calculate the velocity after penetrating the first plank:
The bullet loses one-fifth of its velocity when it penetrates the first plank. Therefore, the final velocity after penetrating the first plank is:
v1=u−15u=45u
3. Use the equation of motion for the first plank:
We apply the equation of motion:
v2=u2−2as1
Substituting v1 and u:
(45u)2=u2−2as1
Simplifying this gives:
1625u2=u2−2as1
Rearranging the equation:
2as1=u2−1625u2=925u2
Thus, we find:
s1=950au2
4. Calculate the velocity after penetrating the second plank:
The bullet comes to a stop after penetrating the second plank, so its final velocity v2=0 and initial velocity u2=45u.
5. Use the equation of motion for the second plank:
Again applying the equation of motion:
v2=u2−2as2
Substituting v2 and u2:
0=(45u)2−2as2
Simplifying gives:
0=1625u2−2as2
Rearranging:
2as2=1625u2
Thus, we find:
s2=825au2
6. Find the ratio of the thickness of the planks:
Now we can find the ratio s1s2:
s1s2=950au2825au2
The u2 and a cancel out:
s1s2=950⋅258=9⋅2550⋅8=225400=916
Final Answer:
The ratio of the thickness of the planks s1s2=916.
Let the initial velocity of the bullet as it leaves the rifle barrel be v=u.
The bullet loses one-fifth of its velocity when it penetrates the first plank. Therefore, the final velocity after penetrating the first plank is:
v1=u−15u=45u
We apply the equation of motion:
v2=u2−2as1
Substituting v1 and u:
(45u)2=u2−2as1
Simplifying this gives:
1625u2=u2−2as1
Rearranging the equation:
2as1=u2−1625u2=925u2
Thus, we find:
s1=950au2
The bullet comes to a stop after penetrating the second plank, so its final velocity v2=0 and initial velocity u2=45u.
Again applying the equation of motion:
v2=u2−2as2
Substituting v2 and u2:
0=(45u)2−2as2
Simplifying gives:
0=1625u2−2as2
Rearranging:
2as2=1625u2
Thus, we find:
s2=825au2
Now we can find the ratio s1s2:
s1s2=950au2825au2
The u2 and a cancel out:
s1s2=950⋅258=9⋅2550⋅8=225400=916
The ratio of the thickness of the planks s1s2=916.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples15videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.125videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
Having gone through a plank of thickness h, a bullet changed its velocity from v0 to v1. Find the time of motion of the bullet on the plank, assuming the resistance force to be proportional to the square of the velocity.
View SolutionA 10 g bullet is fried at a plank od wood with a speed of 200m/s. After passing through the plank which is 1.0 m thick the speed of the bullet reduces to 100m/s. Find the average resistance offered by the plank.
View SolutionA bullet fired into a fixed target loses half of its velocity after penetrating 3 cm . How much further it will penetrate before coming to rest assuming that it faces constant resistance to motion?
View SolutionA bullet loses 1/20 of its velocity in passing through a plank. What is the least number of plank required to stop the bullet .
View SolutionA bullet of mass 5 g moving at a speed of 200 m/s strikes a rigidly fixed wooden plank of thickness 0.2m normally and passes through it losing half of its kinetic energy. If it again strikes an identical rigidly fixed wooden plank and passes through it, assuming the same resistance in the two planks the ratio of the thermal energies produced in the two planks is
View SolutionA bullet when fixed at a target with a velocity of 100ms−1, penetrates one metre into it. If the bullet is fired with the same velocity as a similar target with a thickness 0.5 metre, then it will emerge from it with a velocity of
View SolutionA bullet moving with a speed of 100 m/s can just penetrate two planks of equal thickness. Now if the speed is doubled, then the number of such planks required to stop the bullet will be
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
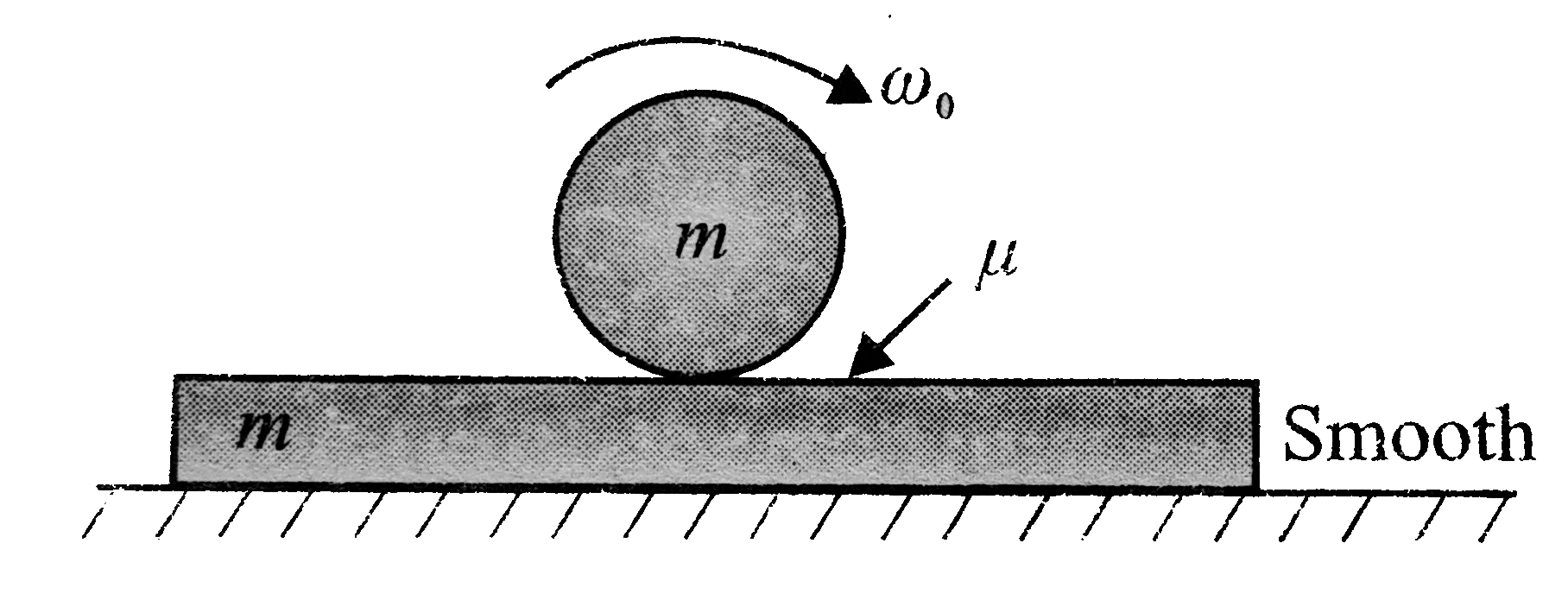
Find the time t at which the pure roiling startsView SolutionA plank of mass M and length L is placed at rest on a smooth horizontal surface. A small block of mass m is projected with a velocity v0 from the left end of it as shown in figure. The coefficient of friction between the block and the plank is m, and its value is such that the block becomes stationary with respect to the plank before it reaches the other end.

a. Find the time and common velocity when relative sliding between the block and the plank stops.
b. Find the work done by the friction force on the block during the period it slides on the plank. Is the work positive or negative?
c. Calculate the work done on the plank during the same period. Is the work positive or negative?
d. Also, determine the net work done by friction, Is it positive or negative?View SolutionA bullet moving with a speed of 100ms−1 can just penetrate into two planks of equal thickness. Then the number of such planks, if speed is doubled will be .
View Solution

