Having gone through a plank of thickness h, a bullet changed its velocity from v0 to v1. Find the time of motion of the bullet on the plank, assuming the resistance force to be proportional to the square of the velocity.
The correct Answer is:t=h(v0−v)v0V In (v0V)
To solve the problem of finding the time of motion of a bullet as it passes through a plank of thickness h, we will follow these steps:
Step 1: Understand the relationship between force and velocity
The resistance force F acting on the bullet is proportional to the square of its velocity v. Therefore, we can express this as:
F=−kv2
where k is a constant of proportionality, and the negative sign indicates that the force opposes the motion.
Step 2: Relate force to acceleration
Using Newton's second law, we know that:
F=ma
where m is the mass of the bullet and a is its acceleration. Since F=−kv2, we can write:
ma=−kv2
This implies:
a=−kmv2
Step 3: Express acceleration in terms of velocity
We can express acceleration a as:
a=dvdt
Thus, we have:
dvdt=−kmv2
Step 4: Rearrange and integrate
Rearranging the equation gives:
dvv2=−kmdt
Now, we will integrate both sides. The left side will be integrated from v0 to v1 (initial to final velocity), and the right side will be integrated from 0 to T (time of motion):
∫v1v0dvv2=−km∫T0dt
Step 5: Perform the integration
The integral on the left side yields:
(−1v)v1v0=−kmT
This simplifies to:
−1v1+1v0=−kmT
or:
1v0−1v1=kmT
Step 6: Relate displacement to velocity
Next, we relate the displacement ds to the velocity:
a=dvdt=vdvds
Thus, we can write:
−kv2=vdvds
This simplifies to:
−kv=dvds
Step 7: Integrate with respect to displacement
Rearranging gives:
dvv=−kds
Integrating from v0 to v1 and 0 to h:
∫v1v0dvv=−k∫h0ds
This yields:
ln(v1v0)=−kh
or:
k=−ln(v1v0)h
Step 8: Substitute k back into the time equation
Substituting k into the time equation gives:
1v0−1v1=−ln(v1v0)h⋅T
Rearranging for T:
T=h(1v0−1v1)−ln(v1v0)
Final Result
Thus, the time of motion of the bullet through the plank is given by:
T=h(v1−v0)v1v0ln(v0v1)
The resistance force F acting on the bullet is proportional to the square of its velocity v. Therefore, we can express this as:
F=−kv2
where k is a constant of proportionality, and the negative sign indicates that the force opposes the motion.
Using Newton's second law, we know that:
F=ma
where m is the mass of the bullet and a is its acceleration. Since F=−kv2, we can write:
ma=−kv2
This implies:
a=−kmv2
We can express acceleration a as:
a=dvdt
Thus, we have:
dvdt=−kmv2
Rearranging the equation gives:
dvv2=−kmdt
Now, we will integrate both sides. The left side will be integrated from v0 to v1 (initial to final velocity), and the right side will be integrated from 0 to T (time of motion):
∫v1v0dvv2=−km∫T0dt
The integral on the left side yields:
(−1v)v1v0=−kmT
This simplifies to:
−1v1+1v0=−kmT
or:
1v0−1v1=kmT
Next, we relate the displacement ds to the velocity:
a=dvdt=vdvds
Thus, we can write:
−kv2=vdvds
This simplifies to:
−kv=dvds
Rearranging gives:
dvv=−kds
Integrating from v0 to v1 and 0 to h:
∫v1v0dvv=−k∫h0ds
This yields:
ln(v1v0)=−kh
or:
k=−ln(v1v0)h
Substituting k into the time equation gives:
1v0−1v1=−ln(v1v0)h⋅T
Rearranging for T:
T=h(1v0−1v1)−ln(v1v0)
Thus, the time of motion of the bullet through the plank is given by:
T=h(v1−v0)v1v0ln(v0v1)
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -J ) Aakash Challengers Questions
12 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Example
24 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -H ) Multiple True - False Type Questions (Identify the correct combination of true (T) and false (F) of the given three statements.)
8 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
A motor boat of mass m moves along a lake with velocity V0. At the moment t=0 the engine of the boat is shut down. Assuming the resistance of water is proportional to the velocity of the boat →F=−r→v
Q. The velocity (v) of the motor boat as a function of the distance (s) covered with the shutdown engine is
View SolutionA bullet leaving the muzzle of a rifle barrel with a velocity v penetrates a plank and loses one-fifth of its velocity. It then strikes second plank, which it just penetrates through. Find the ratio of the thickness of the planks, supposing the average resistance to the penetration is same in both the cases.
View SolutionA gun fires N bullets per second, each of mass m with velocity v. The force exerted by the bullets on the gun is :
View SolutionA bullet losses 1/n of its velocity in passing through a plank. What is the least number of plancks required to stop the bullet ? (Assuming constant retardation)
View SolutionA body of mass m = 4 kg starts moving with velocity v0 in a straight line is such a way that on the body work is being done at the rate which is proportional to the square of velocity as given by P=βv2 where β=0.6932. Find the time elapsed in seconds before velocity of body is doubled.
View SolutionA plank of mass M and length L is placed at rest on a smooth horizontal surface. A small block of mass m is projected with a velocity v0 from the left end of it as shown in figure. The coefficient of friction between the block and the plank is m, and its value is such that the block becomes stationary with respect to the plank before it reaches the other end.

a. Find the time and common velocity when relative sliding between the block and the plank stops.
b. Find the work done by the friction force on the block during the period it slides on the plank. Is the work positive or negative?
c. Calculate the work done on the plank during the same period. Is the work positive or negative?
d. Also, determine the net work done by friction, Is it positive or negative?
View SolutionA 5.0g bullet moving at 100m/s strikes a log. Assume that the bullet undergoes uniform deceleration and stops in 6.0cm. Find (a) the time taken for the bullet to stop, (b) the impulse on the log and (c) the average force experienced by the log.
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.
View SolutionA bullet travelling with a velocity of 16 m/s penetrates a tree trunk and comes to rest in 0.4 m. Find the time taken during the retardation.
View SolutionA small block of mass m is plced over a long plank of mass M the coefficient of friction between then is μ ground is smooth At t=0m is given a velocity v1 and M a velocity v2(>v1) as shown in figure After this M is maintained at constant celeration a(<μg)
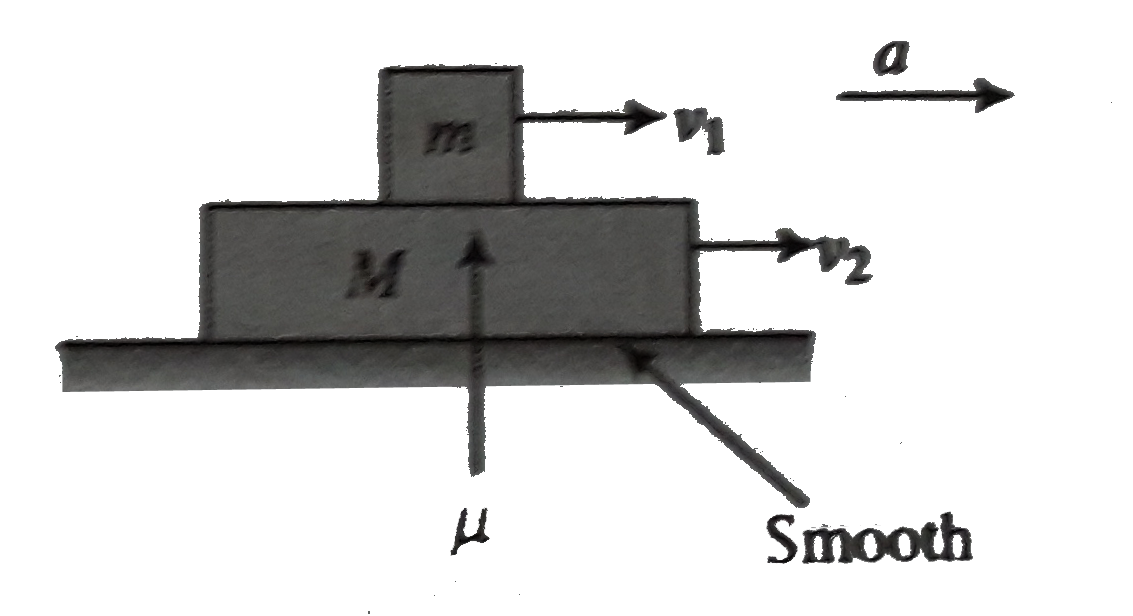
Initially there will be some relative motion between the block and the plank ,but after some time relative motion will cease and velocities of both will become
Draw the velocity of block as a function of time.
View Solution
