A small sphere tied to the string of length $0.8 m$ is describing a vertical circle so that the maximum and minimum tensions in the string are in the ratio $3 : 1$ . The fixed end of the string is at a height of $5.8 m$ above ground.
(a) Find the velocity of the sphere at the lowest position.

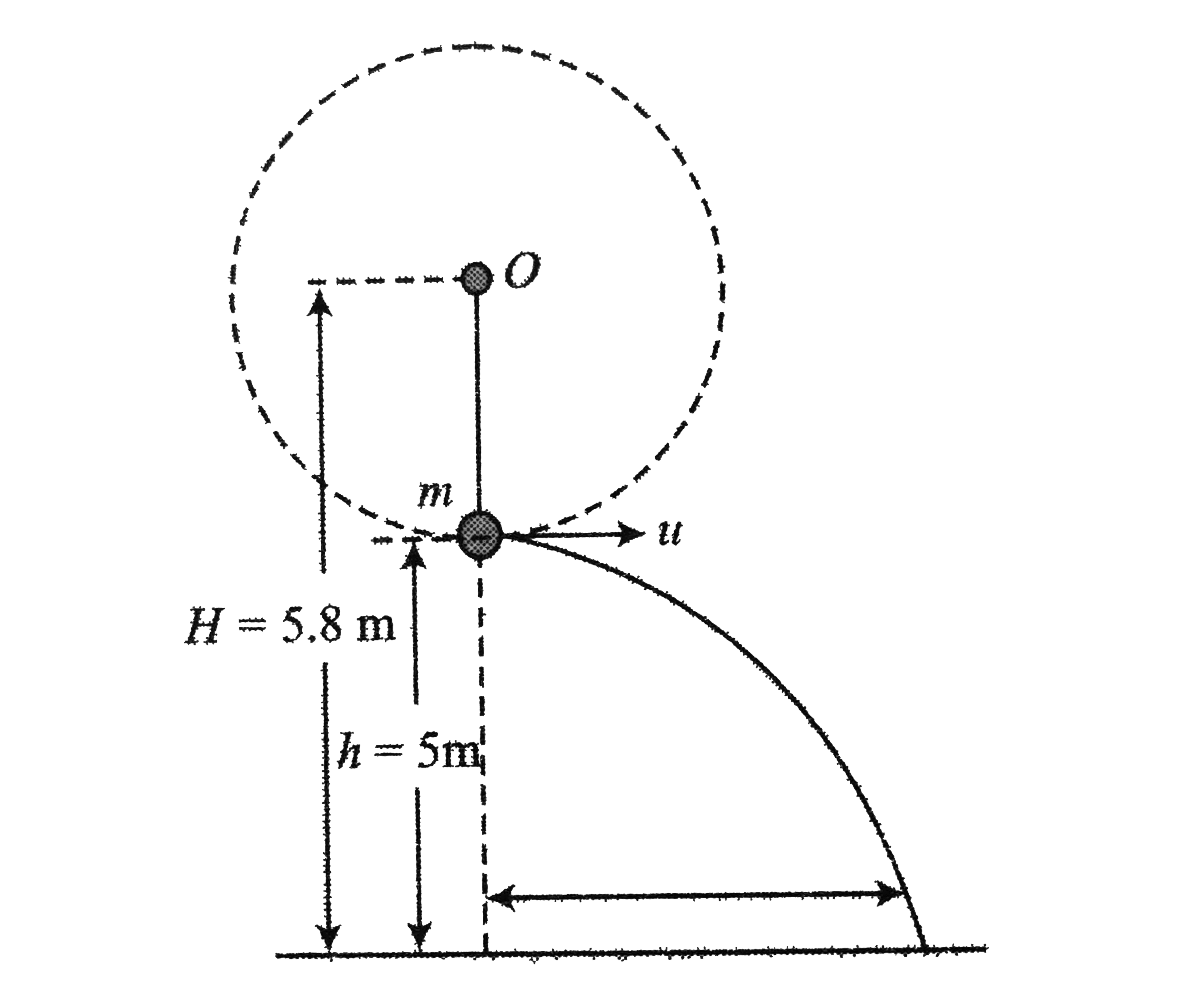
(b) If the string suddenly breaks at the lowest position, when and where will the sphere hit the ground?

Video Solution

Text Solution

Verified by Experts

a. Let $u$ and $v$ the speeds of sphere at the bottom and the top positions and $m$ be the mass.
radius of circle=length of string $= r = 0.8 m$ .
$T_{b} =$ tension at the bottom or the maximum tension
$T_{t} =$ tension at the top or the minimum tension

$T_{b} - m g = \frac{m v^{2}}{r}$
$T_{t} + m g = \frac{m v^{2}}{r} \Rightarrow T_{b} = 3 T_{t}$
$(\frac{μ^{2}}{r} + m g) = 3 (\frac{m v^{2}}{r} - m g)$
$\Rightarrow (3 v^{2} - u^{2}) = 4 r g$ (i)
Using conservation of energy,
loss in KE from bottom to the top=gain in GPE
$\frac{1}{2} μ^{2} - \frac{1}{2} m v^{2} = m g (2 r)$
$\Rightarrow v^{2} = u^{2} - 4 r g$ (ii)
Using (i) and (ii), we get
$3 (u^{2} - 4 g r) - u^{2} = 4 g r$
$\Rightarrow 2 u^{2} = 16 r g$
$\Rightarrow u = \sqrt{8 r g} \Rightarrow \sqrt{8 (0.8) 10} = 8 m s^{- 1}$
b. After breaking away from the string, the sphere moves along a parabolic path, and strikes the ground at G.
Vertical displacement of sphere
$S_{y} = 5.8 - 0.8 = 5 m$
Let t=time after which the sphere hits the ground.
$\Rightarrow S_{y} = 0 t + \frac{1}{2} g t^{2} \Rightarrow t = \sqrt{\frac{2 S_{y}}{g}} = 1 s$
The horizontal displacement $= x = u t = 8 \times 1 = 8 m$ .
Hence, the sphere hits the ground $1 s$ after breaking off the string and at the poing G.

Updated on:21/07/2023