The maximum and minimum tension in the string whirling in a circle of radius 2.5 m with constant velocity are in the ratio 5:3 then its velocity is
10ms
7ms
15ms
5ms
The correct Answer is:A
To solve the problem, we need to analyze the forces acting on the mass at the highest and lowest points of the circular motion and use the given ratio of tensions to find the velocity. Here’s the step-by-step solution:
Step 1: Understand the Forces Acting on the Mass
When the mass is at the lowest point:
- The tension in the string (T1) acts upwards.
- The weight of the mass (mg) acts downwards.
- The centripetal force required for circular motion is provided by the net force, which is T1 - mg.
At the lowest point, the equation of motion can be written as:
T1=mg+m⋅r⋅ω2
where r is the radius and ω is the angular velocity.
When the mass is at the highest point:
- The tension in the string (T2) acts upwards.
- The weight of the mass (mg) acts downwards.
- The centripetal force is provided by the tension and the weight, so we have:
T2+mg=m⋅r⋅ω2
This can be rearranged to:
T2=m⋅r⋅ω2−mg
Step 2: Set Up the Ratio of Tensions
We know from the problem that the ratio of maximum tension (T1) to minimum tension (T2) is given as:
T1T2=53
Substituting the expressions for T1 and T2, we have:
mg+m⋅r⋅ω2m⋅r⋅ω2−mg=53
Step 3: Cross Multiply and Simplify
Cross multiplying gives us:
3(mg+m⋅r⋅ω2)=5(m⋅r⋅ω2−mg)
Expanding both sides:
3mg+3m⋅r⋅ω2=5m⋅r⋅ω2−5mg
Step 4: Rearranging the Equation
Rearranging the terms gives:
3mg+5mg=5m⋅r⋅ω2−3m⋅r⋅ω2
8mg=2m⋅r⋅ω2
Step 5: Cancel Out m and Solve for ω²
Dividing both sides by 2m:
8g2=r⋅ω2
4g=r⋅ω2
Thus, we find:
ω2=4gr
Step 6: Relate Velocity to Angular Velocity
We know that:
v=r⋅ω
Squaring both sides gives:
v2=r2⋅ω2
Substituting ω2 from above:
v2=r2⋅4gr
This simplifies to:
v2=4g⋅r
Taking the square root:
v=√4g⋅r
Step 7: Substitute Values for g and r
Given:
- g=10m/s2
- r=2.5m
Substituting these values:
v=√4⋅10⋅2.5
v=√100
v=10m/s
Final Answer
The velocity of the whirling mass is 10m/s.
---
When the mass is at the lowest point:
- The tension in the string (T1) acts upwards.
- The weight of the mass (mg) acts downwards.
- The centripetal force required for circular motion is provided by the net force, which is T1 - mg.
T1=mg+m⋅r⋅ω2
where r is the radius and ω is the angular velocity.
- The tension in the string (T2) acts upwards.
- The weight of the mass (mg) acts downwards.
- The centripetal force is provided by the tension and the weight, so we have:
T2+mg=m⋅r⋅ω2
This can be rearranged to:
T2=m⋅r⋅ω2−mg
We know from the problem that the ratio of maximum tension (T1) to minimum tension (T2) is given as:
T1T2=53
mg+m⋅r⋅ω2m⋅r⋅ω2−mg=53
Cross multiplying gives us:
3(mg+m⋅r⋅ω2)=5(m⋅r⋅ω2−mg)
3mg+3m⋅r⋅ω2=5m⋅r⋅ω2−5mg
Rearranging the terms gives:
3mg+5mg=5m⋅r⋅ω2−3m⋅r⋅ω2
8mg=2m⋅r⋅ω2
Dividing both sides by 2m:
8g2=r⋅ω2
4g=r⋅ω2
Thus, we find:
ω2=4gr
We know that:
v=r⋅ω
Squaring both sides gives:
v2=r2⋅ω2
Substituting ω2 from above:
v2=r2⋅4gr
This simplifies to:
v2=4g⋅r
Taking the square root:
v=√4g⋅r
Given:
- g=10m/s2
- r=2.5m
v=√4⋅10⋅2.5
v=√100
v=10m/s
The velocity of the whirling mass is 10m/s.
Similar Questions
For a particle rotating in a vertical circle with uniform speed, the maximum and minimum tension in the string are in the ratio 5 : 3. If the radius of vertical circle is 2 m, the speed of revolving body is (g=10m/s2)
View SolutionA particle of mass m attached to an inextensible light string is moving in a vertical circle of radius r. The critical velocity at the highest point is v0 to complete the vertical circle. The tension in the string when it becomes horizontal is
View SolutionA small sphere tied to the string of length 0.8m is describing a vertical circle so that the maximum and minimum tensions in the string are in the ratio 3:1. The fixed end of the string is at a height of 5.8m above ground.
(a) Find the velocity of the sphere at the lowest position.
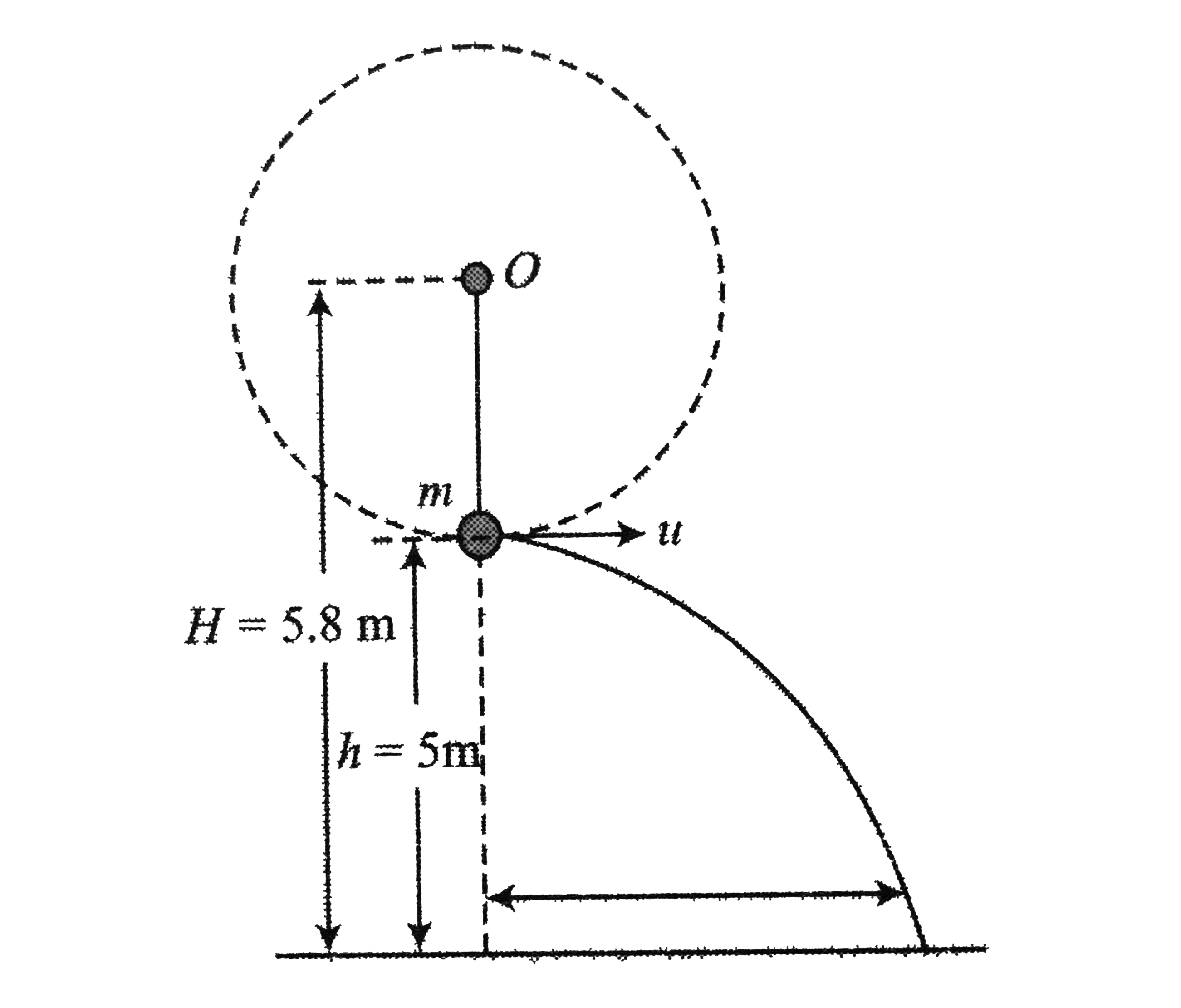
(b) If the string suddenly breaks at the lowest position, when and where will the sphere hit the ground?
View SolutionA particle is moving along a circle of radius 20cm, with a linear velocity of 2m//s. Calculate the angular velocity of the particle.
View SolutionA particle is moving along a circle of radius 20cm, with a linear velocity of 2m//s. Calculate the angular velocity of the particle.
View SolutionA stone of of mass 0.25 kg tied to the end of a string is whirled round in a circle of radius 1.5 m with a speed of 40rev/min in a horizontal plane What is the tension in the string ? What is the maximum speed with which the stone can be whirled around If the string can withstand a maximum tension of 200 N ?
View SolutionA stone of mass 1kg is tied with a string and it is whirled in a vertical circle of radius 1 m. If tension at the highest point is 14 N, then velocity at lowest point will be
View SolutionA stone of 1 kg tied up with 10/3 m long string rotated in a vertical circle. If the ratio of maximum and minimum tension in string is 4 then speed of stone at highest point of circular path will be ( g=10ms2)
View SolutionWhen tension of a string is increased by 2.5 N, the initial frequency is altered in the ratio of 3:2. The initial tension in the string is
View SolutionCalculate the magnitude of linear acceleration of a particle moving in a circle of radius 0.5 m at the instant when its angular velocity is 2.5 rad s–1 and its angular acceleration is 6rads−2.
View Solution
