A block A of mass is attached with a spring having force constant . The other end of the spring is fixed to a rough plane, inclined at with horizontal and having coefficient of friction . Block A is gently placed on the plane such that the spring has no tension. Then block A is released slowly. Calculate elongation of the spring when equilibrium is achieved. Now an inextensible thread is connected with block A and passes below pulley C and over pulley D, as shown in figure. Other end of the thread is connected with another block B of mass . Block B is resting over a table and thread is loose. If the table collapse suddenly and B falls freely through , the thread becomes taut, calculate combined speed of blocks at that instant, and maximum elongation of spring in the process of motion. .
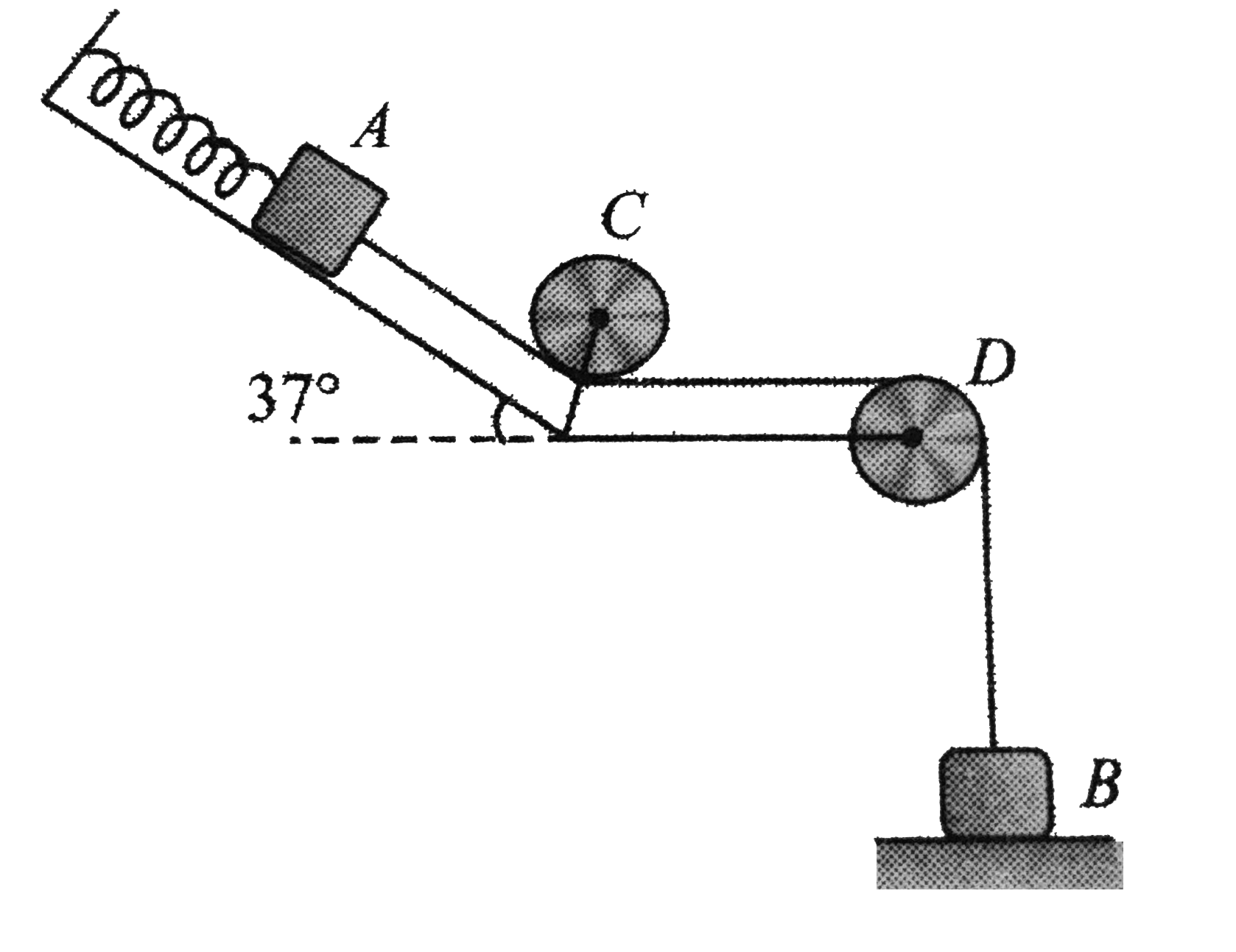
Since the block is released slowly, therefore, it starts to slide down the plane till equilibrium of forces is achieved.

Let at that instant elongation of spring be , then tension in it is
Considering free body diagram of block,
(i)
(ii)
From Eq. (i) and (ii),
When table collapses, first block B falls freely under gravity through height . Therefore, its speed just before the string becomes taut is
Now block A is jerked into motion and a large tension (for a very small time interval) is developed in string due to which both the blocks A and B experience numerically equal impulses.
Let its magnitude be J and let the combined speed of blocks be v.
Then for block A, (iii)
for block B, (iv)
From equation (iii) and (iv)
At the instant of maximum elongation of spring, blocks are momentarily at rest.
Let distance moved by the blocks be x from the instant when blocks A was jerked into motion to the instant of maximum elongation of the spring.
According to law of consevation of energy,
Loss of potential energy of A+Loss of potential energy of B+
Loss of kinetic energy of blocks=Increase in energy stored in spring+Work done by the block A against friction.
or
Maximum elongation of spring= Its initial elongation
Further elongation
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.125videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.225videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)4videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
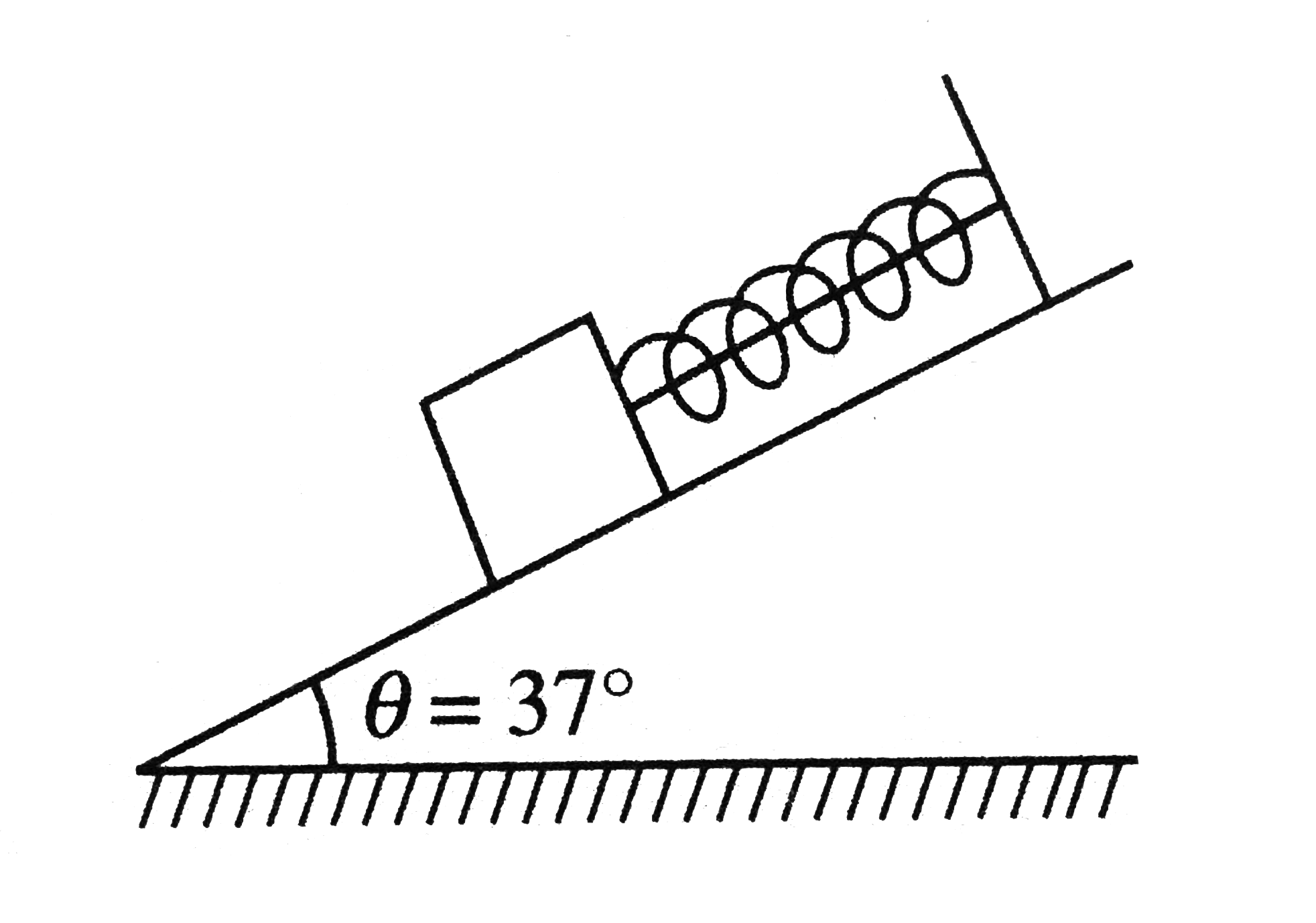
A small block of mass m=1kg is attached with one end of the spring of force constant K=110Nm−1. Other end of the spring is fixed to a rough plane having coefficient of friction μ=0.2. The spring is kept in its natural length by an inextensible thread ties between its ends as shown in figure. If the thread is burnt, calculate the elongation of the spring when the block attains static equilibrium position.
 View Solution
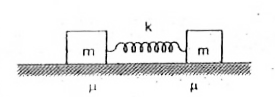
View SolutionTwo blocks each having mass m is attached to each other with a spring having force constant k. The system is placed on a rough horizontal surface having coefficient of friction μ. The maximum initial compression, that can be given to the spring so that when released the blocks do not move is
 View Solution
View SolutionA block of mass m attached with a an ideal spring of force constant k is placed on a rough inclined plane having inclination θ with the horizontal and coefficient of friction μ=1/2tanθ, Initially the block is held stationary with the spring in its relaxed state, find the maximum extension in the spring if the block is released.
 View Solution
View SolutionA block of mass m is attached with a massless spring of force constant k. The block is placed over a rough inclined surface for which the coefficient of friction is μ=34. The minimum value of M required to move the block up the plane is (Neglect mass of string, mass of pulley and friction in pulley)
 View Solution
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionA block of mass m is attached with a massless spring of force constant K. the block is placed over a rough inclined surface for which the coefficient of friction is μ=34 find the minimum value of M required to move the block up the place. (Neglect mass of string and pulley. Ignore friction in pulley).
 . View Solution
. View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is
 View Solution
View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View SolutionA block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
View Solution

