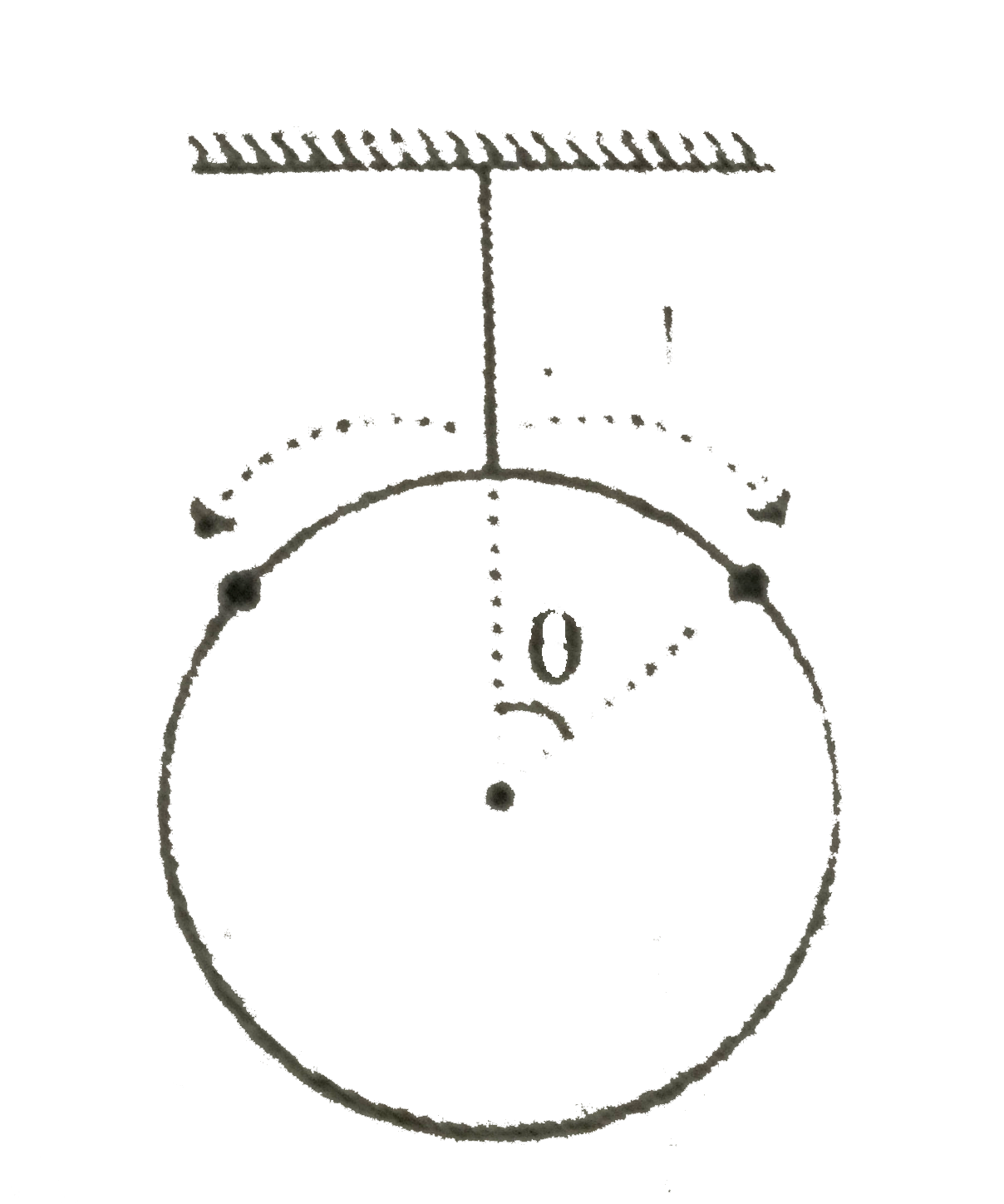
A loop of mass M with two identical rings of mass m at its top hangs from a ceiling by an inextensible string. If the rings gently pushed horizontally in opposite directions, find the angular distance covered by each ring when the tension in the string vanishes for once during their motion.

Video Solution

Text Solution

Verified by Experts

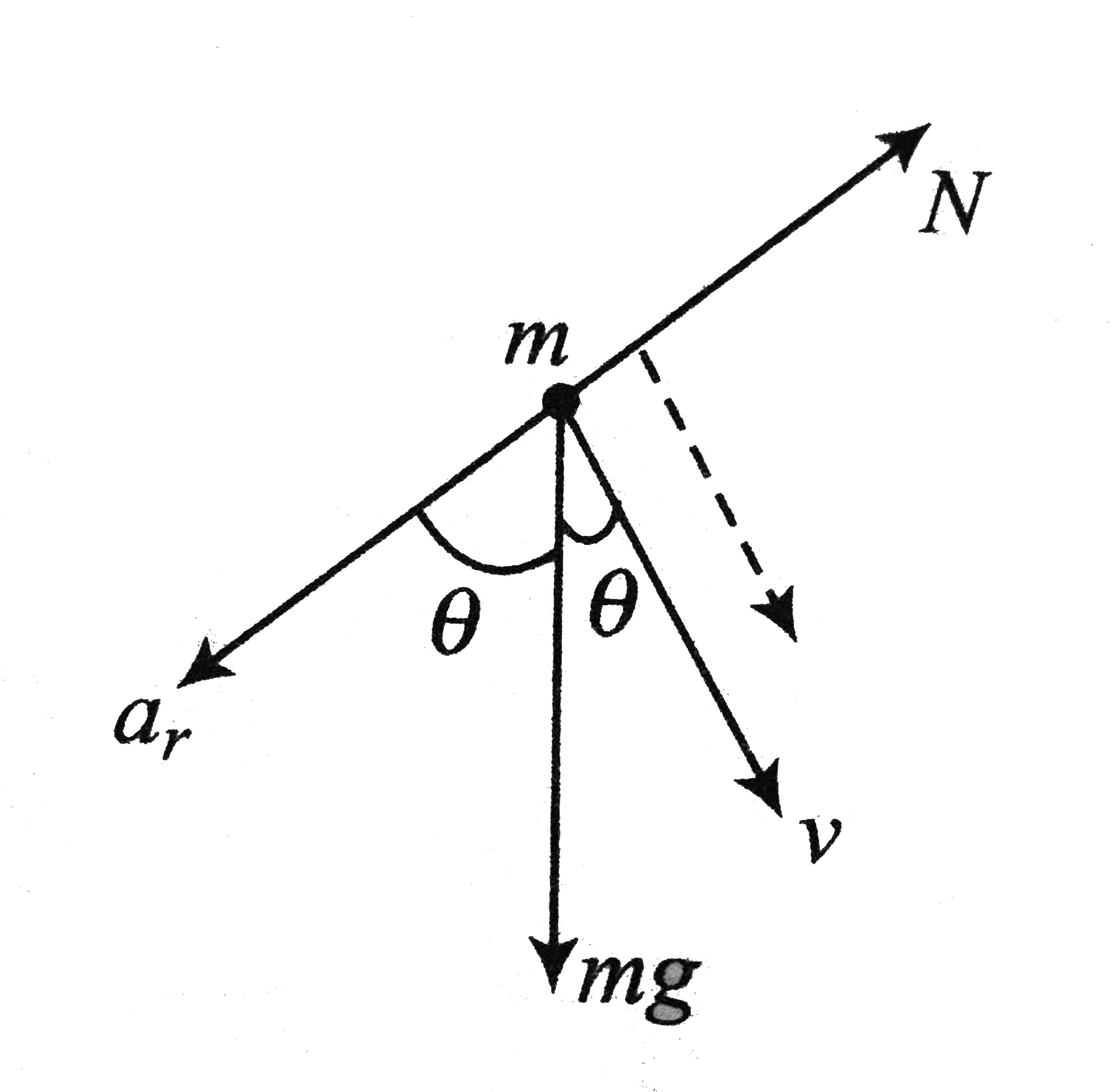
Suppose the string slakens that means its tension T becomes zero when the rings slide through and angle $θ$ with vertical as shown in figure. The speeds of the rings at the angular position $θ$ can be given by conserving its energy between the position 1 and 2

$\Rightarrow Δ P E = Δ K E$
$\Rightarrow m g h = \frac{1}{2} m v^{2}$
$\Rightarrow m g [r - r cos θ] = \frac{1}{2} m v^{2}$
$\Rightarrow v = \sqrt{2 g r (1 - cos θ)}$ (i)
Referring figure, resolving the force acting on the ring radially we obtain

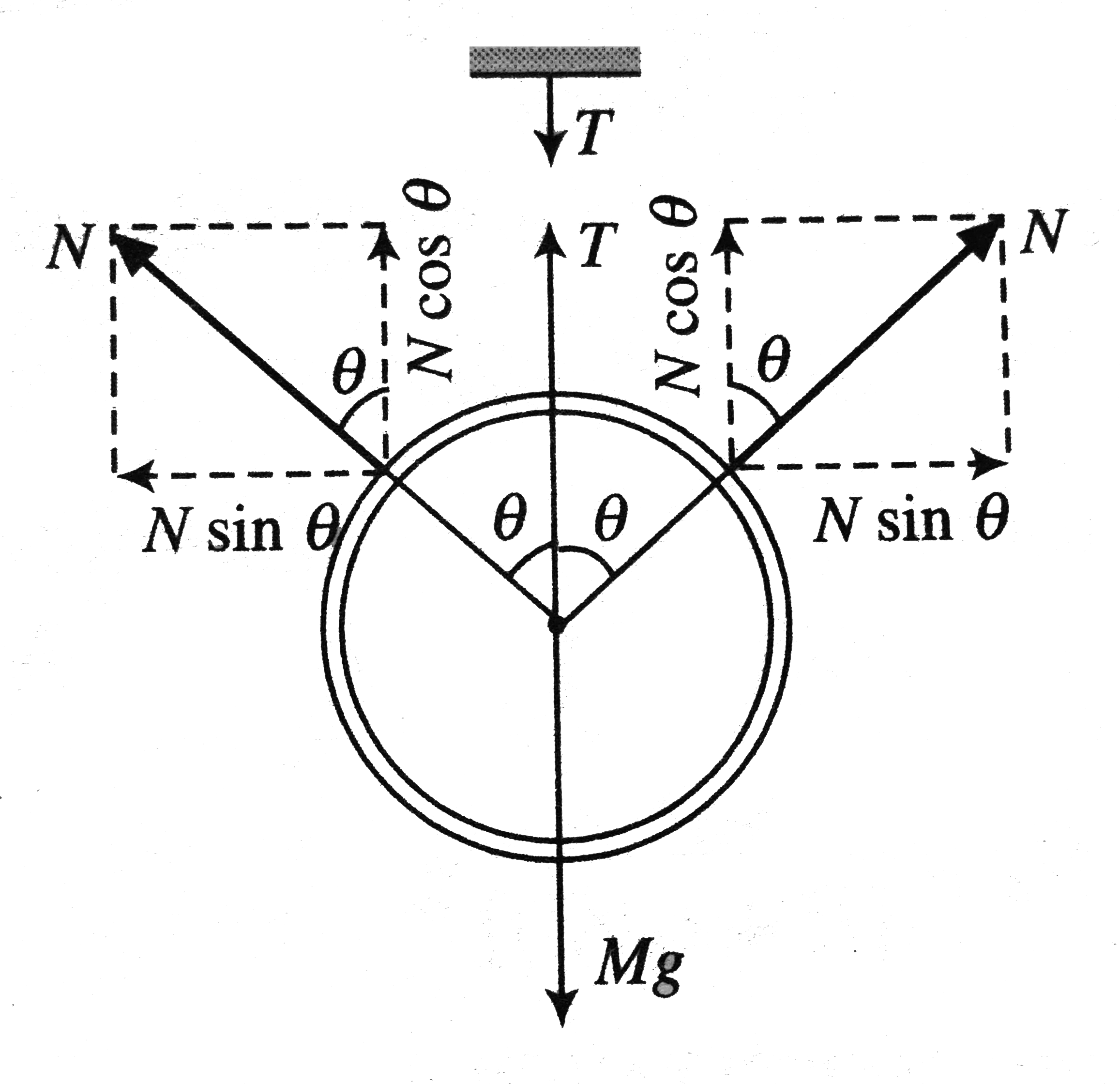
$F_{c p} = m g cos θ + N$
where N is the contacting force between the hoop and the rings.
$m a_{r} = m g cos θ + N$
$\Rightarrow \frac{m v^{2}}{r} = m g cos θ + N$
$\Rightarrow N = \frac{m v^{2}}{r} - m g cos θ$ (ii)
Resolving the forces acting on the hoop for its equilibrium (refer figure we obtain)

$F_{x} = N sin θ - N sin θ = 0$
and $F_{y} = 2 N cos θ + T - M g = 0$
$\Rightarrow 2 N cos θ + T - M g = 0$ ,
Since the string slackens,
$T = 0 \Rightarrow N = \frac{M g}{2 cos θ}$ (iii)
Using Eqs (ii) and (iii),
$\frac{M g}{2 cos θ} = \frac{m v^{2}}{r} - m g cos θ$ (iv)
Using Eqs (i) and (iv),
$\frac{M g}{2 cos θ} = \frac{m}{r} {2 g r (1 - cos θ)} - m g cos θ$
$\Rightarrow 3 {cos}^{2} θ - 2 cos θ + \frac{M}{2 m} = 0$ (v)
$\Rightarrow cos θ = \frac{1}{3} [1 \pm \sqrt{(1 - (3 / 2) (M / m))}$
If $\frac{M}{m} \leq \frac{2}{3}$ , if $\frac{M}{m} > \frac{2}{3}$
$cos θ$ in imaginary, which means the string cannot be slakened.
If $\frac{M}{m} = \frac{2}{3}$ , the quadratic equation (v) has one root, which means the string is slacken at $θ = {cos}^{- 1} (1 / 3)$ .

|

Updated on:21/07/2023

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-WORK, POWER & ENERGY-Solved Examples

Home
Ask Doubt
Profile