Figure shows a smooth track, a part of which is a circle of radius r. A block of mass m is pushed against a spring of spring constant k fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P, where the radius of the track is horizontal.
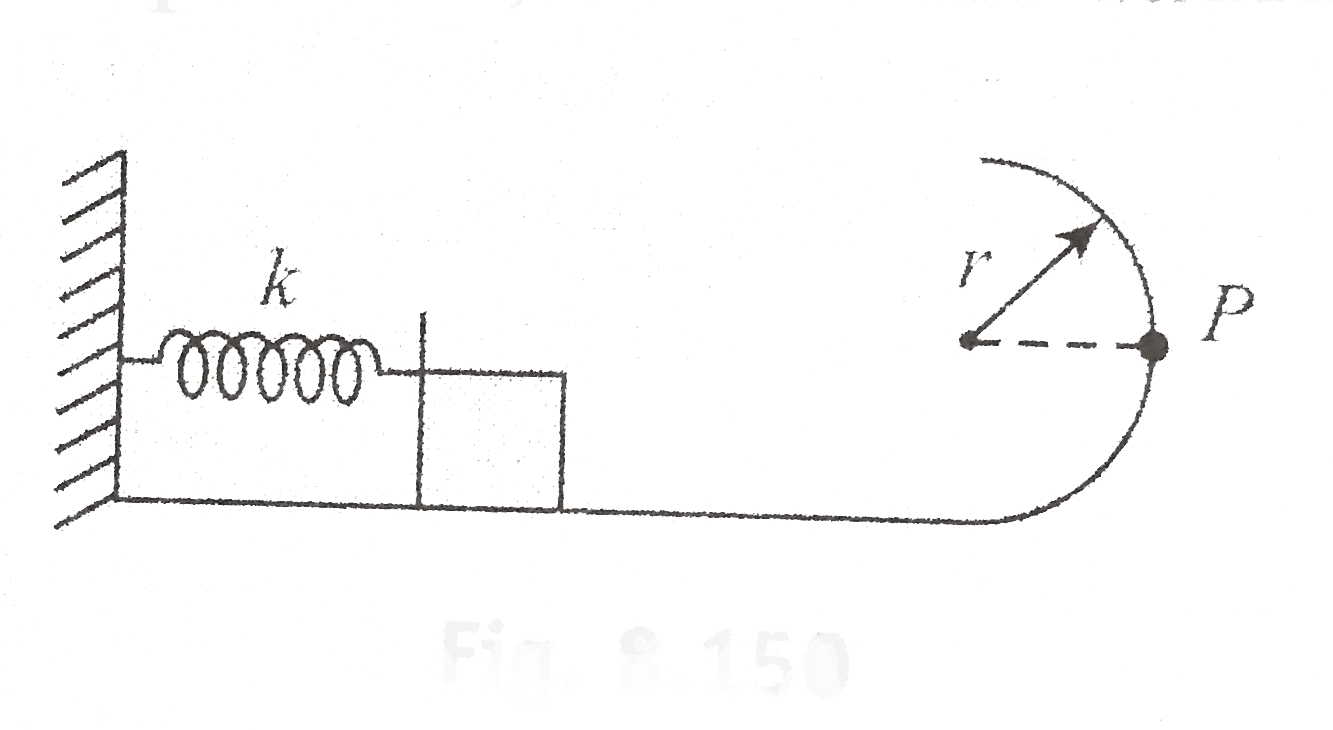
Let the initial compression of the spring be x and when the spring is released, the stored compressional energy in the spring is given to the block and it shoots on the track, which ends in a vertical circle of radius r. When the mass reaches the point P, the weight of block at this point is in vertical downward direction and the block pushes the track with the only force mv2/r.
At P, the force on track should be equal to the weight of the block, thus
(mv2r)=mg or v=√rg
Now we apply work-energy theorem from starting point of the spring to the final P for the block.
As initial kinetic energy of the block is zero and at P for the block.
As initial kinetic energy of the block is zero and at P it is mv2/2,
thus we have
0+12kx2−mgr=12mv2
12kx2−mgr=12m(rg)
kx2=3mgr⇒x=√3mgrk
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.5
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective
23 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.3
26 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A block of mass m is pushed against a spring of spring constant k fixed at the end to a wall. The block can side on a frictionless table as shown in figure. The natural length of the spring is L0 and it is compressed ti half its natural length when the block is relesed. Find teh velocity of the block aa s function of its distance x from the wall .

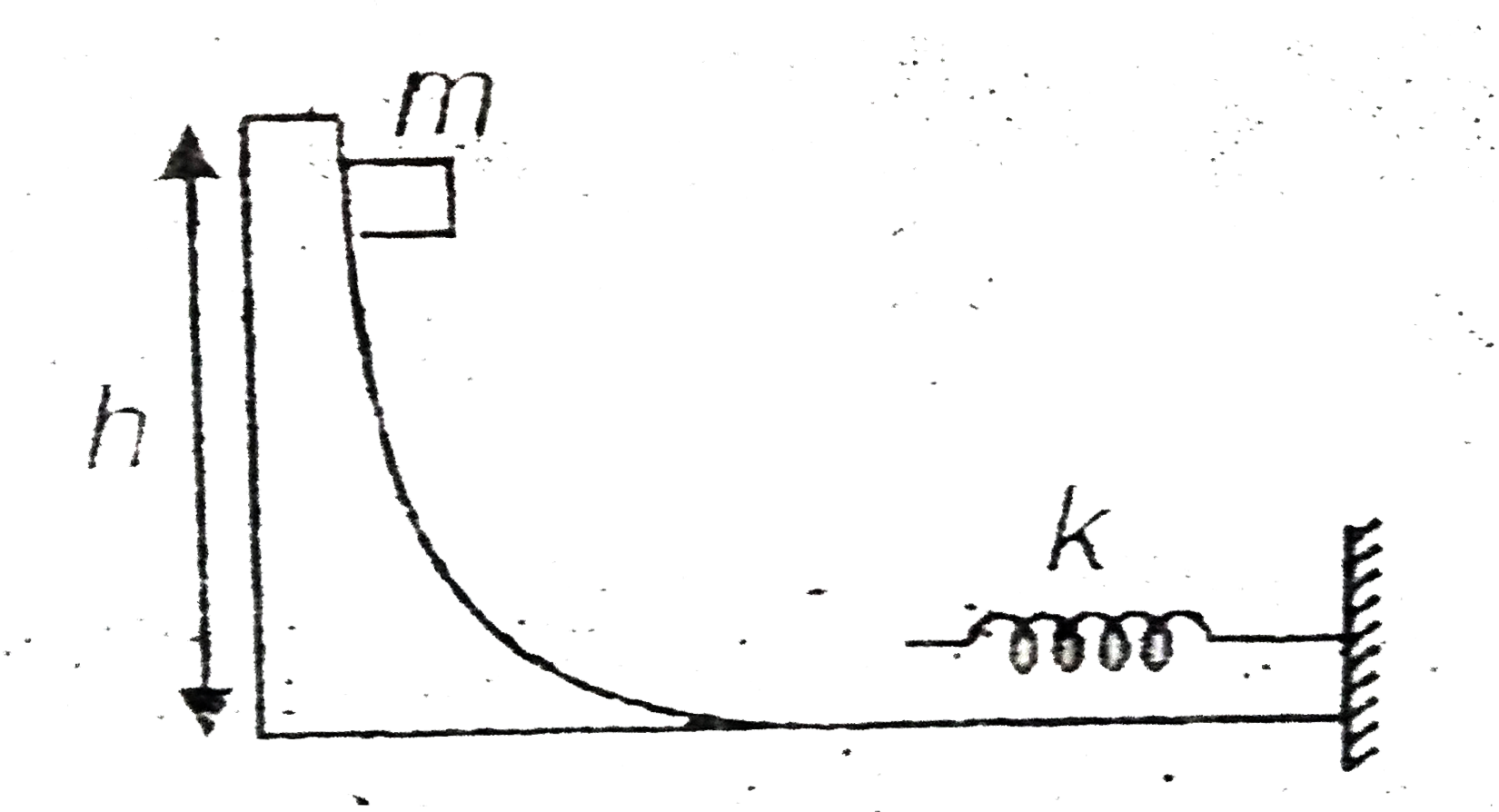
View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)
View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionTwo blocks of masses m and M connected by a light spring of stiffness k, are kept on a smooth horizontal surface as shown in figure. What should be the initial compression of the spring so that the system will be about to break off the surface, after releasing the block m1?
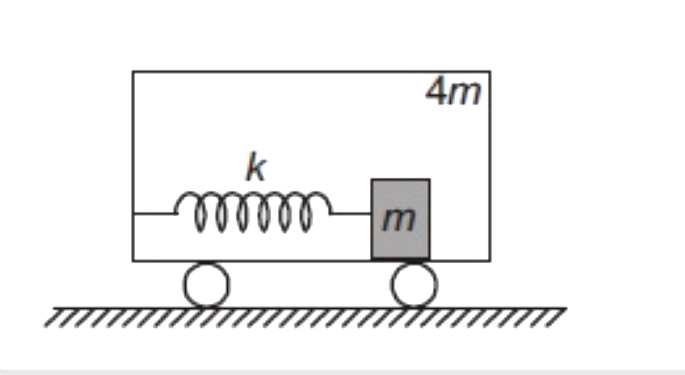
View SolutionA block of mass m is attached to a cart of mass 4m through spring of spring constant k as shown in the figure. Friction is absent everywhere. The time period of oscillations of the system, when spring is compressed and then released, is
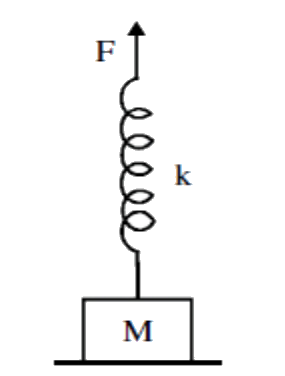
View SolutionA block of mass m is kept on a rough horizontal surface and is attached with a massless spring of force constant k. The minimum constant force applied on the other end of the spring of lift the block is
View SolutionA small block of mass 500 gm is pressed against a horizontal spring fixed at one end to a distance of 10 cm. when released, the block moves horizontally till it leaves the spring. Where it will hit the ground 5 m below the spring. (Take k = 100 N/m of spring)
View SolutionA small block of mass 100 g is pressed again a horizontal spring fixed at one end to compress the sprign through 5.0 cm. The spring constant is 100 N/m. When released, the block moves hroizontally till it leaves the spring. Where will it hit the ground 2 m below the spring?
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionA block of mass m is suddenly released from the top of a spring of stiffness constant k.
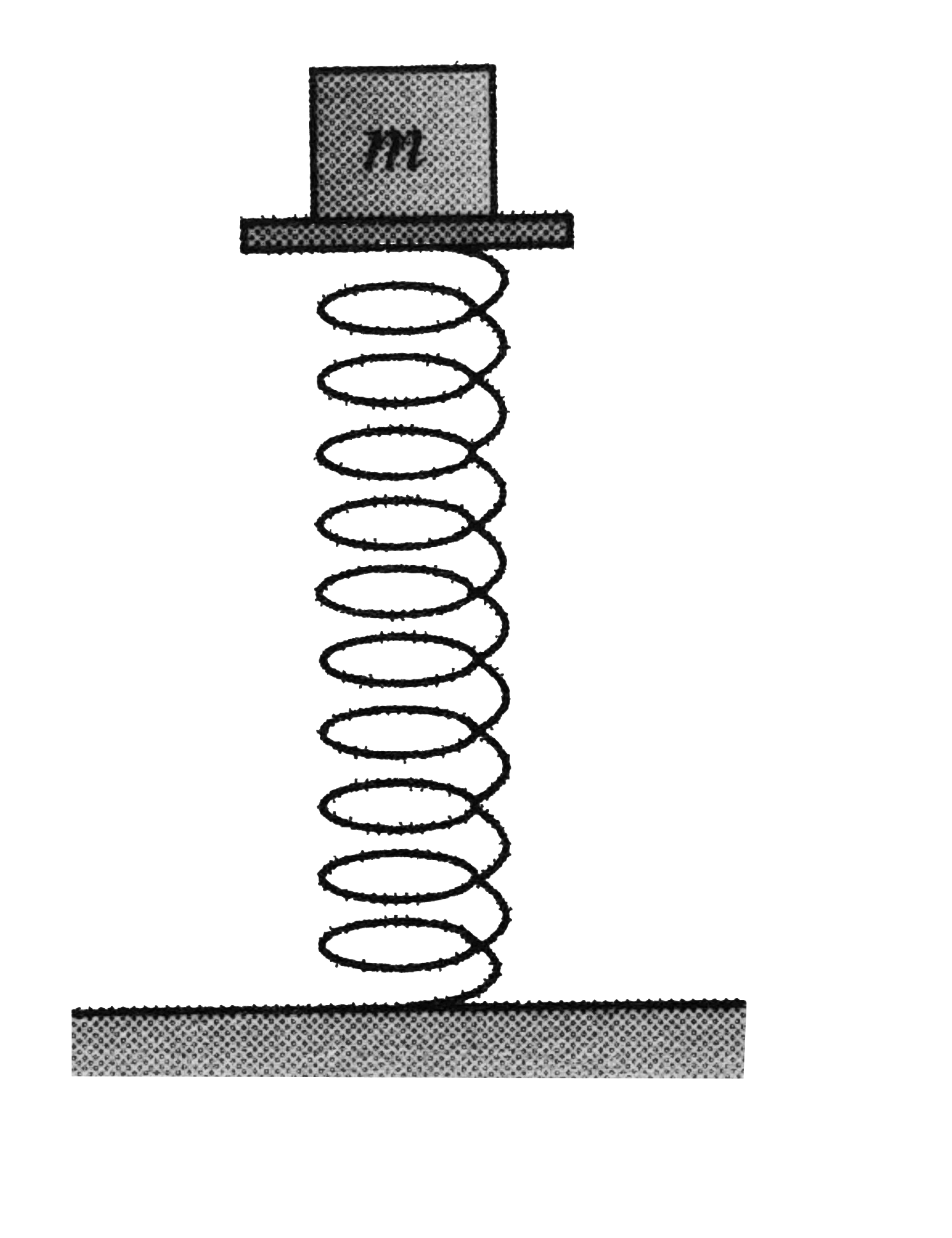
a. Find the acceleration of block just after release.
b. What is the compression in the spring at equilibrium.
c. What is the maximum compression in the spring.
d. Find the acceleration of block at maximum compression in the spring.
View Solution