Two unequal masses are tied together with a cord with a compressed spring in between. The cord is burned.
Which of the following energies is conserved for the system?
(a) Kinetic energy
(b) Potential energy
(c) Mechanical energy
(d) None of these
The correct Answer is:C
To solve the problem, we need to analyze the situation involving two unequal masses tied together with a cord and a compressed spring in between them. When the cord is burned, we need to determine which type of energy is conserved in the system.
1. Understand the Initial State:
- Initially, the two masses m1 and m2 are at rest, meaning their kinetic energy is zero.
- The spring is compressed, which means there is potential energy stored in the spring, given by the formula PE=12kx2, where k is the spring constant and x is the compression distance.
Hint: Identify the initial energies in the system before any action takes place.
2. Action of Burning the Cord:
- When the cord is burned, the spring will decompress, causing the two masses to move apart.
- As the spring decompresses, the potential energy stored in the spring will convert into kinetic energy of the two masses.
Hint: Consider the transformation of energy types when the cord is burned.
3. Kinetic Energy After the Release:
- After the cord is burned, the masses will have some kinetic energy as they move apart. The kinetic energy of the system can be expressed as:
KE=12m1v21+12m2v22
- Here, v1 and v2 are the velocities of masses m1 and m2 respectively.
Hint: Remember that kinetic energy will increase as the spring releases its stored energy.
4. Conservation of Energy:
- The total mechanical energy of the system is the sum of the kinetic energy and the potential energy. Initially, the total mechanical energy is purely potential energy (from the spring).
- After the cord is burned, the potential energy decreases as the spring decompresses, while the kinetic energy of the masses increases.
- Since there are no external forces acting on the system (assuming no friction or air resistance), the total mechanical energy is conserved.
Hint: Think about the principle of conservation of energy in a closed system.
5. Conclusion:
- The potential energy of the spring is converted into kinetic energy of the masses, but the total mechanical energy remains constant throughout the process.
- Therefore, the correct answer is that mechanical energy is conserved in the system.
Final Answer:
The energy that is conserved for the system is mechanical energy.
- Initially, the two masses m1 and m2 are at rest, meaning their kinetic energy is zero.
- The spring is compressed, which means there is potential energy stored in the spring, given by the formula PE=12kx2, where k is the spring constant and x is the compression distance.
- When the cord is burned, the spring will decompress, causing the two masses to move apart.
- As the spring decompresses, the potential energy stored in the spring will convert into kinetic energy of the two masses.
- After the cord is burned, the masses will have some kinetic energy as they move apart. The kinetic energy of the system can be expressed as:
KE=12m1v21+12m2v22
- Here, v1 and v2 are the velocities of masses m1 and m2 respectively.
- The total mechanical energy of the system is the sum of the kinetic energy and the potential energy. Initially, the total mechanical energy is purely potential energy (from the spring).
- After the cord is burned, the potential energy decreases as the spring decompresses, while the kinetic energy of the masses increases.
- Since there are no external forces acting on the system (assuming no friction or air resistance), the total mechanical energy is conserved.
- The potential energy of the spring is converted into kinetic energy of the masses, but the total mechanical energy remains constant throughout the process.
- Therefore, the correct answer is that mechanical energy is conserved in the system.
The energy that is conserved for the system is mechanical energy.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Integer14videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (sinble Correct )19videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct25videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
Two unequal masses are ties together with a cord with a compressed spring in between.
Which one is correct?View SolutionTwo unequal masses are ties together with a cord with a compressed spring in between.
When the cord is burnt with a match releasing the spring, the two masses fly apart with equalView Solution
Knowledge Check
- Question 1 - Select One
In which of the following structures vocal cords are located?
AoesophagusBLarynxCPharynxDBronchi
Which of the following is used in tyre cords ?
View SolutionA shell in its flight, explodes into four unequal parts. Which of the following is conserved?
View SolutionWhich of the following is currently used as a tyre cord?
View SolutionTwo identical blocks each of mass 1kg are joined together with a compressed spring. When the system is released the two blocks appear to be moving with unequal speeds in the opposite directions as shown in fig.
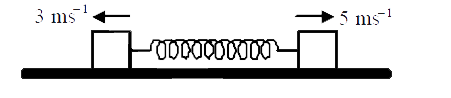
Choose the correct statement -View SolutionTwo blocks A and B are joined together with a compressed spring. When the system is released, the two bloks appear to be moving with unequal speeds in the opposite directions as shown in figure.
Select incorrect statements(s) :
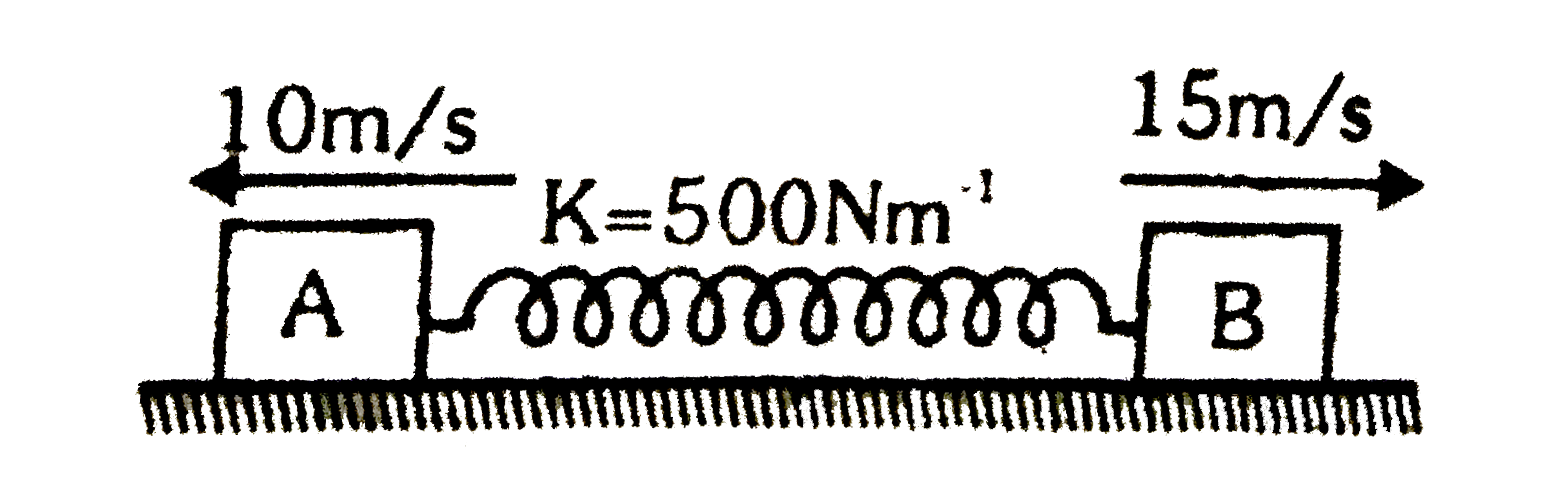 View Solution
View SolutionTwo blocks of masses M and 3M are placed on a horizontal, frictionless surface. A light spring is attached to one of them and the blocks are pushed together with the spring between them. A cord initially holding the blocks together is burned, after that, the block of mass 3M moves to the right with a speed of 2.00m/s. (a) What is the velocity of the block of mass M. (b) Find the system's original elastic potential energy, taking M=0.350kg. (c) Is the original energy in the spring or in the cord? Explain your answer. (d) Is momentum of the system conserved in the bursting apart process? How can it be with large forces acting? How can it be with no motion beforehand and plenty of motion afterward?
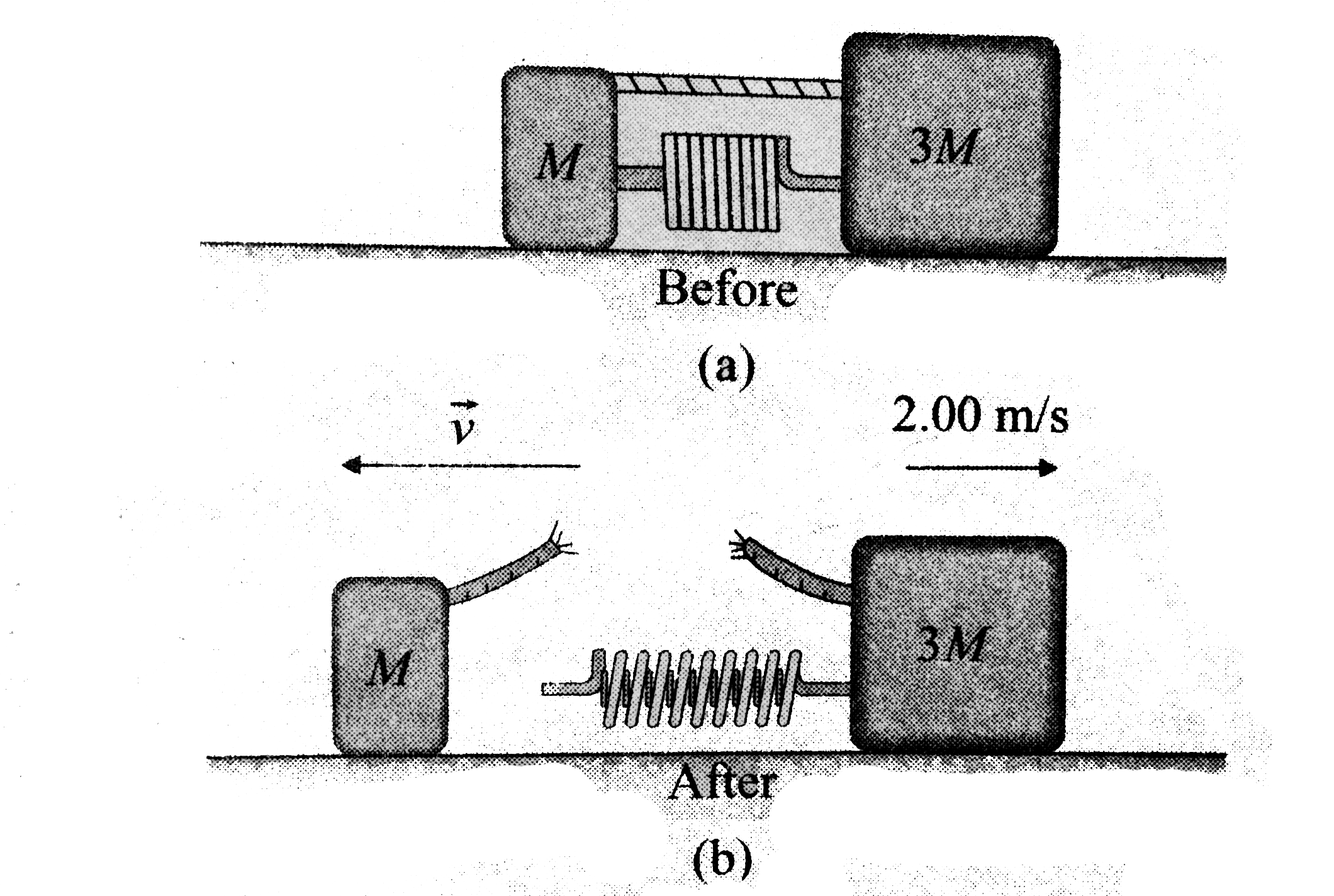 View Solution
View SolutionWhich of the following animals is devoid of notochord and nerve cord in its adult stage ?
View Solution

