A ladder of length l carrying a man of mass m at its end is attached to the basket of a balloon of mass M. The entire system is in equilibrium in the air. As the man climbs up the ladder into the balloon, the balloon descends by a height h.
The potential energy of the man
(a) Increases by mg(l−h)
(b) Increases by mgl
(c) Increases by mgh
(d) Increases by mg(2l−h)
The correct Answer is:A
To solve the problem step by step, we will analyze the situation involving the ladder, the man, and the balloon.
Step 1: Understand the System
We have a ladder of length l with a man of mass m at its end. The ladder is attached to a balloon of mass M. The entire system is in equilibrium in the air.
Hint: Identify the components of the system and their masses.
Step 2: Analyze the Climbing Action
When the man climbs the ladder, he moves upwards. As he climbs, the balloon descends by a height h.
Hint: Consider the conservation of energy and how the movement of the man affects the balloon.
Step 3: Calculate the Potential Energy Change
The potential energy of the man when he climbs to a height l is given by:
ΔPEman=mgh
where h is the height he climbs.
Hint: Remember that potential energy is calculated using the formula PE=mgh.
Step 4: Consider the Balloon's Descent
As the man climbs, the balloon descends by height h. The potential energy lost by the balloon is:
ΔPEballoon=Mgh
Hint: The potential energy change for the balloon is also based on its mass and the height it descends.
Step 5: Set Up the Energy Balance Equation
Since the system is in equilibrium, the work done by the man climbing is equal to the potential energy lost by the balloon:
mgh=Mgh
Hint: This equation represents the balance of energy in the system.
Step 6: Solve for the Potential Energy of the Man
The total potential energy of the man when he climbs up is:
PEman=mgl
The change in potential energy of the man as he climbs is:
ΔPEman=mgl−Mgh
Hint: Calculate the total potential energy considering both the man and the balloon.
Step 7: Conclusion
The potential energy of the man increases by:
ΔPE=mgl−Mgh
Thus, the potential energy of the man increases by this amount as he climbs into the balloon.
Final Answer: The potential energy of the man increases by mgl−Mgh.
We have a ladder of length l with a man of mass m at its end. The ladder is attached to a balloon of mass M. The entire system is in equilibrium in the air.
When the man climbs the ladder, he moves upwards. As he climbs, the balloon descends by a height h.
The potential energy of the man when he climbs to a height l is given by:
ΔPEman=mgh
where h is the height he climbs.
As the man climbs, the balloon descends by height h. The potential energy lost by the balloon is:
ΔPEballoon=Mgh
Since the system is in equilibrium, the work done by the man climbing is equal to the potential energy lost by the balloon:
mgh=Mgh
The total potential energy of the man when he climbs up is:
PEman=mgl
The change in potential energy of the man as he climbs is:
ΔPEman=mgl−Mgh
The potential energy of the man increases by:
ΔPE=mgl−Mgh
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Integer
14 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (sinble Correct )
19 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A ladder of length l carrying a man of mass m at its end is attached to the basket of a balloon of mass M. The entire system is in equilibrium in the air. As the man climbs up the ladder into the balloon, the balloon descends by a height h.
The work done by the man is
View SolutionA man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon
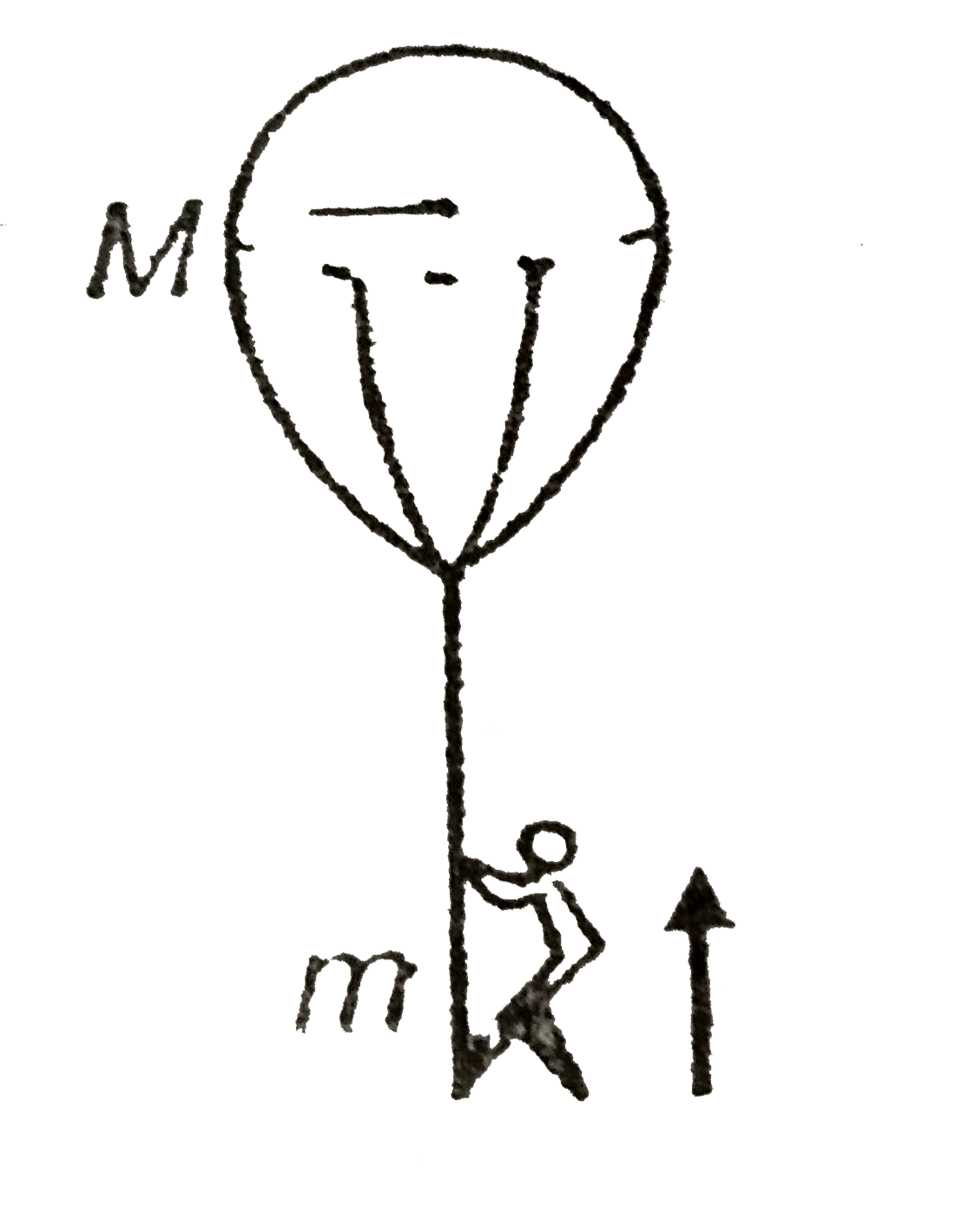
View SolutionA man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon
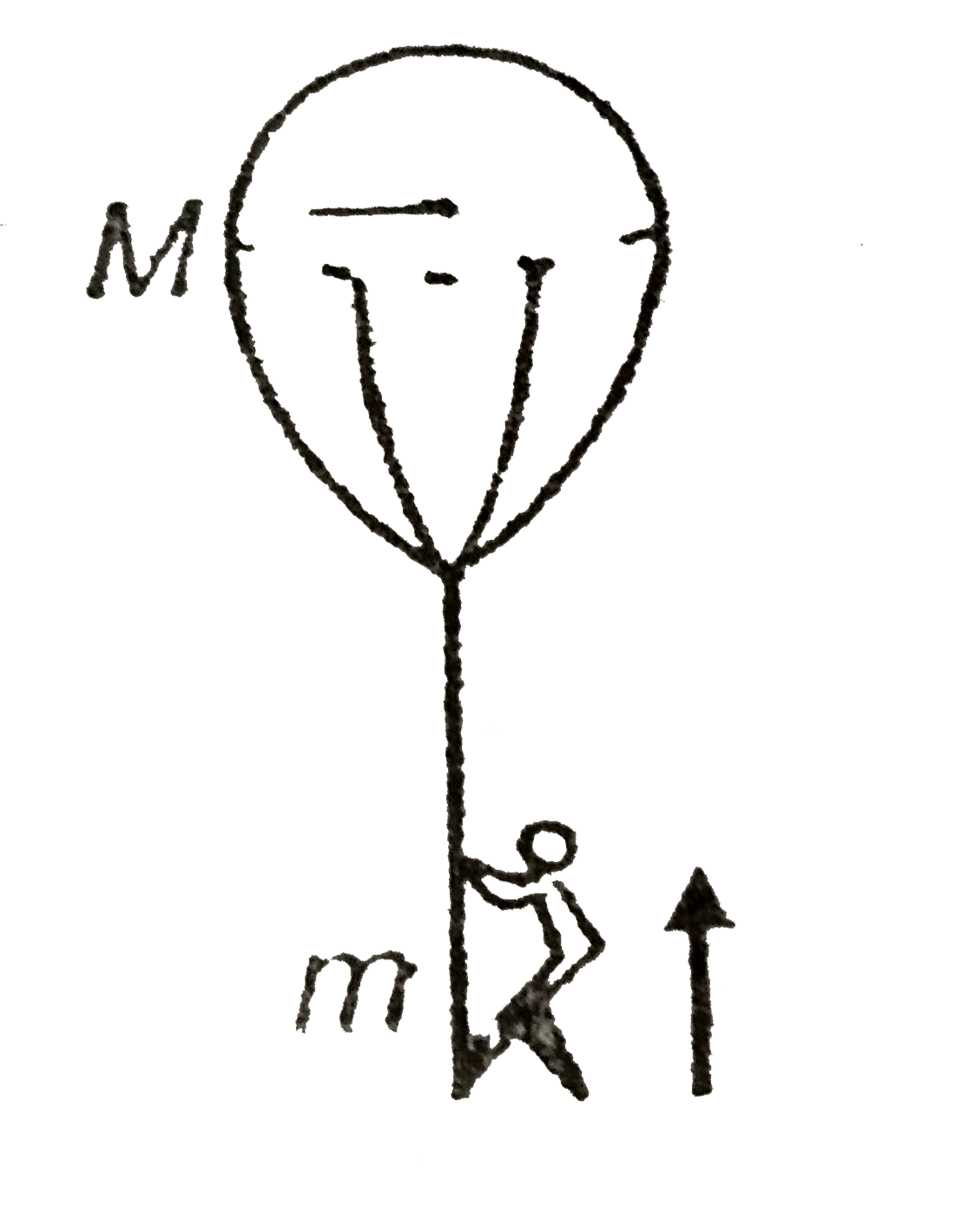
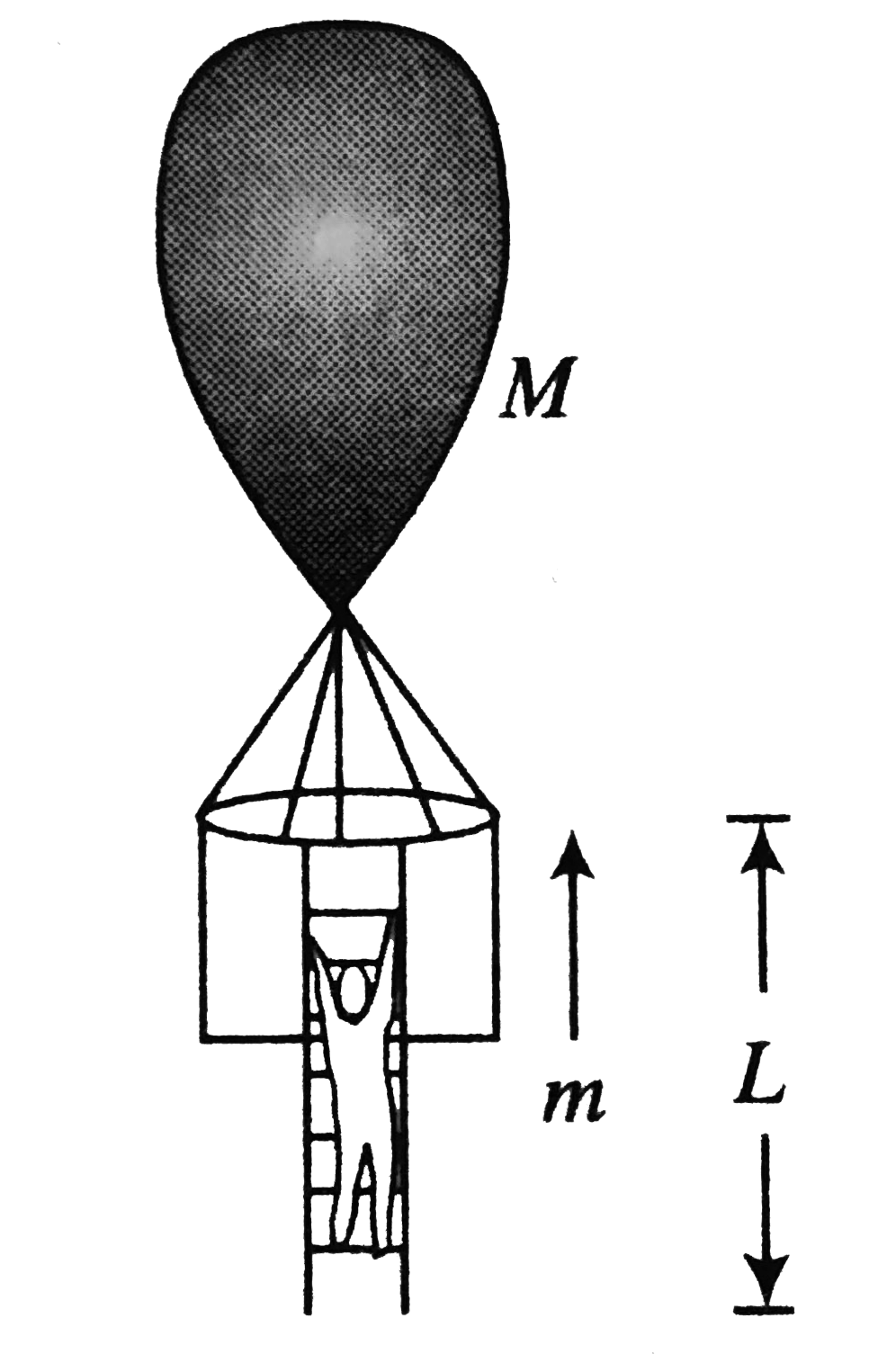
View SolutionA rope ladder of length L is attached to a balloon of mass M. As the man of mass m climbs the ladder into the balloon basket, the balloon comes down by a vertical distance s. Then the increase in potential energy of man divided by the increase in potential energy of balloon is
View SolutionA cart of mass M is tied to one end of a massless rope of length 10m. The other end of the rope is in the hands of a man of mass M2. The entire ststem is on a smooth horizontal surface. If the man pulls the cart by the rope then find the distance by which the man will slip on the horizontal surface before the man and the cart will meet each other.
View SolutionA cart of mass M is tied to one end of a massless rope of length 10m. The other end of the rope is in the hands of a man of mass M. The entire system is on a smooth horizontal surface. The man is at x=0 and the cart at x=10m. If the man pulls the cart by the rope, the man and the cart will meet at the point
View SolutionA man of mass m , standing at the bottom of the staircase of height L climbs it and stands at its top .
View SolutionA man of mass m walks from end A to the other end B of a boat of mass M and length l. The coefficient of friction between the man and the boat is μ an neglect any resistive force between the boat and the water.
View SolutionA man of mass m is standing at one end of of a plank of mass M. The length of the plank is L and it rests on a frictionless horizontal ground. The man walks to the other end of the plank. Find displacement of the plank and man relative to the ground.

View SolutionA man of mass m stands at the left end of a uniform plank of length L and mass M, which lies on a frictionaless surface of ice. If the man walks to the other end of the plank, then by what distance does the plank slide on the ice?
View Solution
