Two graphs of the same projectile motion (in the xy-plane) projected from origin are shown. X-axis is along horizontal direction and y-axis is vertically upwards. Take g=10ms−2.
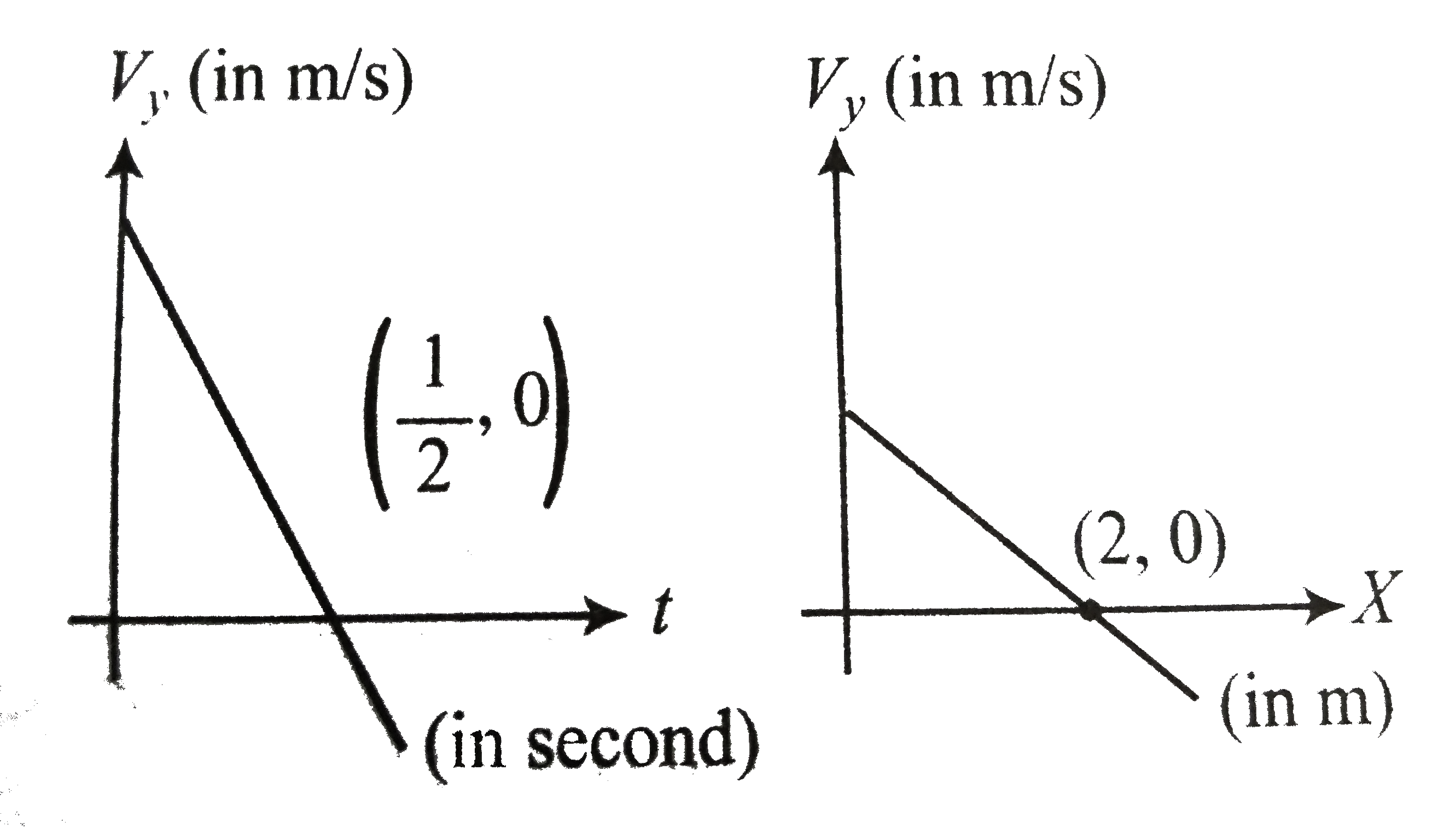 ,
,
Maximum height attained from the point of projection is
1.25 m
12.5 m
2.25 m
None of these
The correct Answer is:A
Time of flight (T) = 1s
2uyg=1s⇒uy=5ms−1
Range (R) = 4m.
(2(ux)(uy)).g=4⇒ux=4ms−1
u=√u2x+u2y=√41ms−1
θ=tan−1(uyux)=tan−1(54)
H=u2y2g=(5)220=54=1.25m.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Integer Type17videos
MISCELLANEOUS KINEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Fill in the blanks4videos
MISCELLANEOUS KINEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Multiple Correct Answer Type26videos
MISCELLANEOUS KINEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type14videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
Similar Questions
Two graphs of the same projectile motion (in the xy-plane) projected from origin are shown. X-axis is along horizontal direction and y-axis is vertically upwards. Take g=10ms−2.
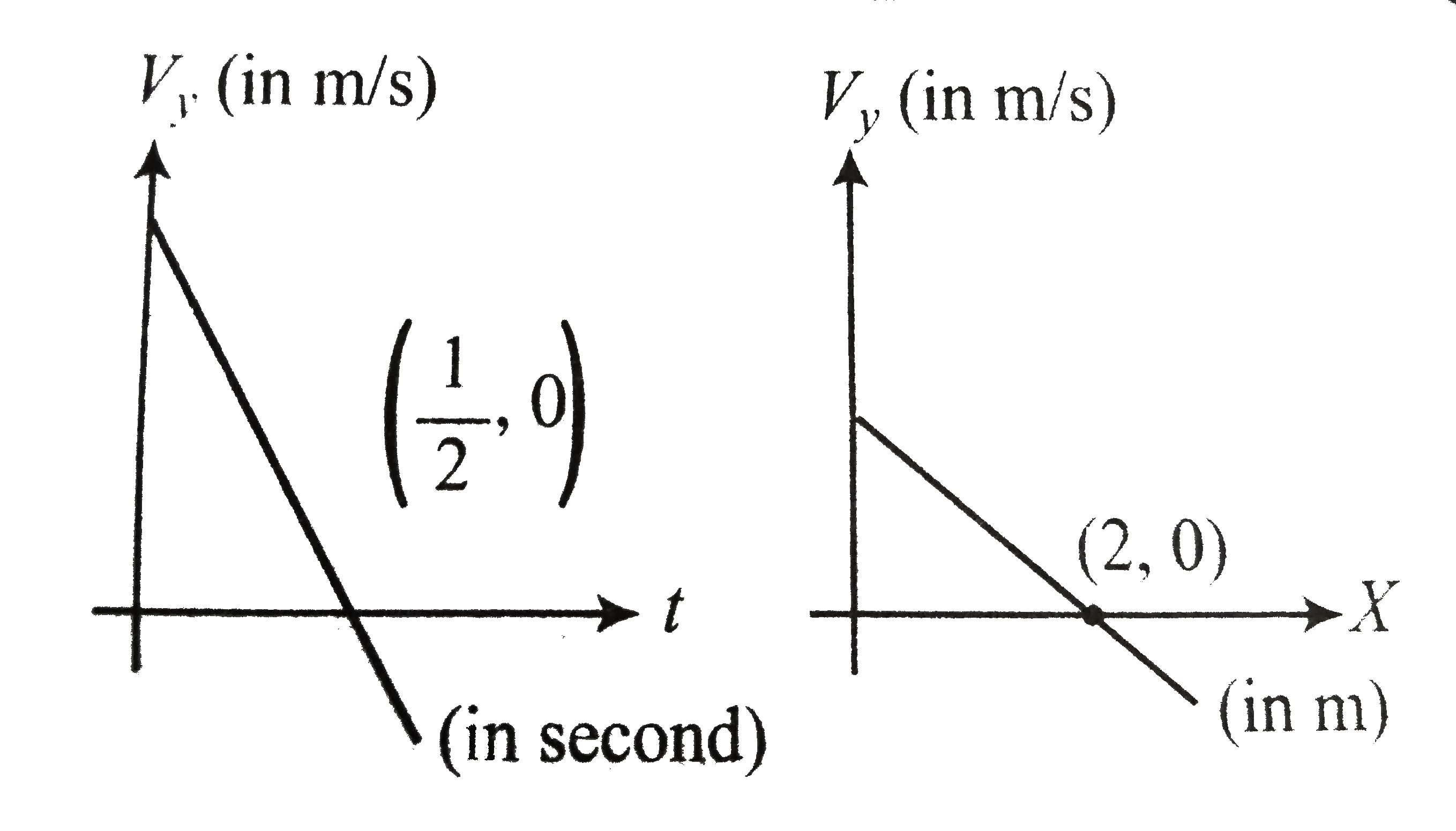 ,
,
The projection speed is :View SolutionTwo graphs of the same projectile motion (in the xy-plane) projected from origin are shown. X-axis is along horizontal direction and y-axis is vertically upwards. Take g=10ms−2.
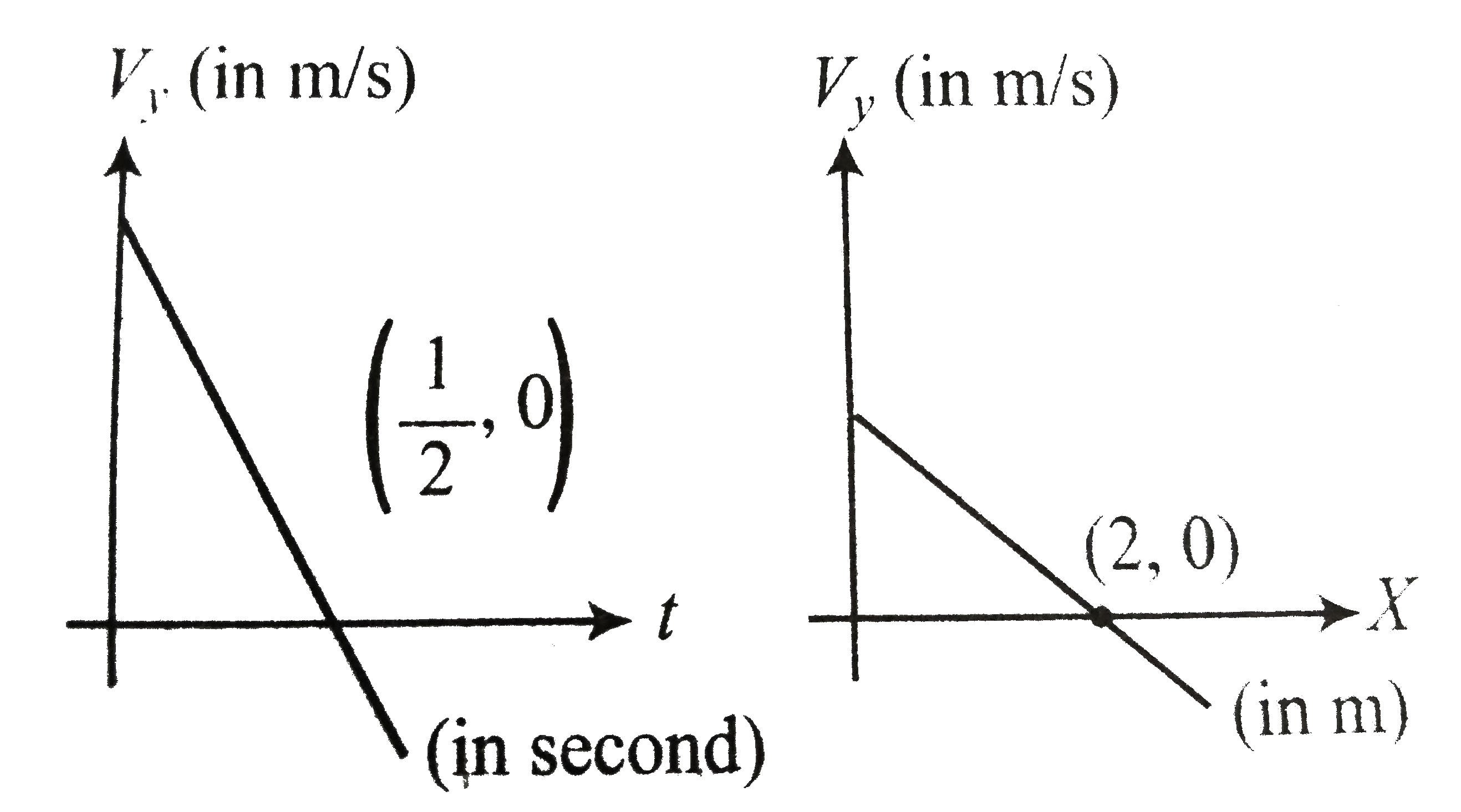
Projection angle with the horizontal is :View SolutionVelocity of a projectile at height 15m from ground is v=(20ˆi+10ˆj)m/s. Here ˆi is in horizontal direction and ˆj is vertically upwards. Then
Maximum height from a ground is ……..mView SolutionA rocket is projected vertically upwards and its time velocity graph is shown in the figure-1.115. The maximum height attained by the rocket is :
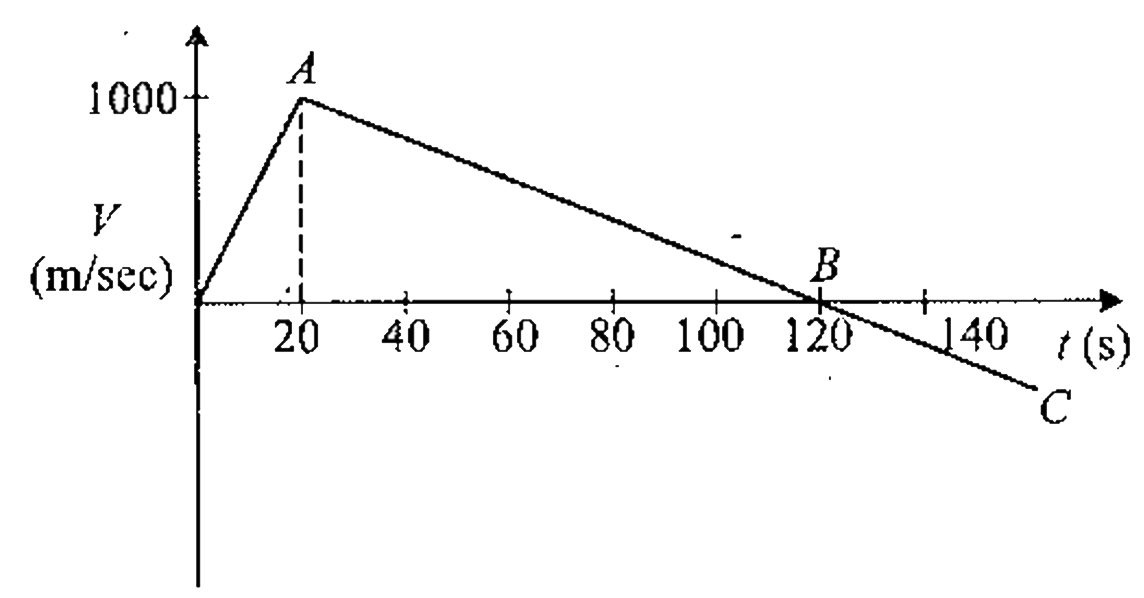 View Solution
View SolutionFor an object projected from ground with speed u horizontal range is two times the maximum height attained by it. The horizontal range of object is
View SolutionA particle is projected from gound At a height of 0.4 m from the ground, the velocity of a projective in vector form is →v=(6ˆi+2ˆj)m/s (the x-axis is horizontal and y-axis is vertically upwards). The angle of projection is (g=10m/s2)
View SolutionMatch the following

A particle is projected from a large fixed incline plane as shown. Here (Vertically downward) take g=10m/s2.
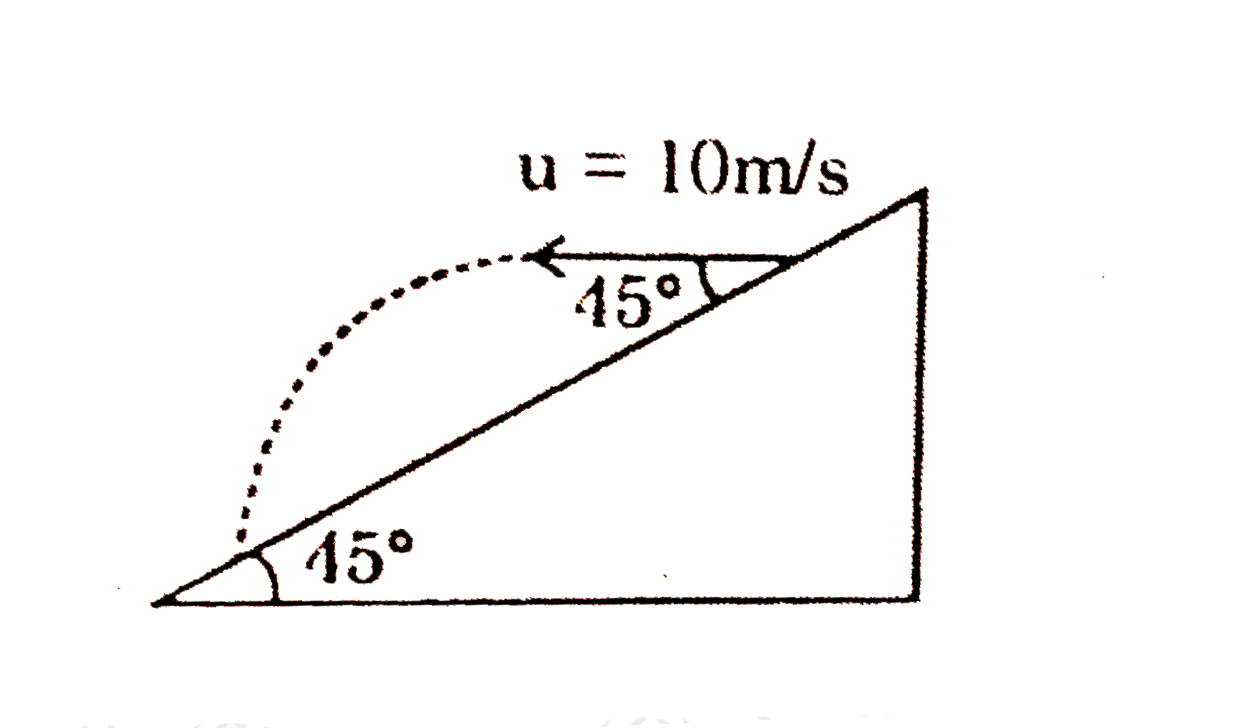 View Solution
View SolutionA projectile is projected from the ground by making an angle of 60∘ with the horizontal. After 1 s projectile makes an angle of 30∘ with the horizontal . The maximum height attained by the projectile is (Take g=10ms−2)
View Solution
A particle is projected from the horizontal x-z plane, in vertical x-y plane where x-axis is horizontal and positive y-axis vertically upwards. The graph of y coordinate of the particle v/s time is as shown . The range of the particle is √3. Then the speed of the projected particle is:View SolutionA regular hexagon of side a=10√3m is kept at horizontal surface as shown in the figure. A particle is projected with velocity Vm/s at an angle θ from point K such that it will just touches the all four corners regular hexagon at B, C, D and E as shown in the figure. If O is the centre of hexagon and x−axis is parallel to horizontal and y−axis is perpendicular to AF and CD side of hexagon then answer the following [take g=10m/s2]
The maximum height from horizontal surface attained by projectile is
 View Solution
View Solution

