A particle is projected from gound At a height of 0.4 m from the ground, the velocity of a projective in vector form is →v=(6ˆi+2ˆj)m/s (the x-axis is horizontal and y-axis is vertically upwards). The angle of projection is (g=10m/s2)
45∘
60∘
30∘
tan−1(3/4)
The correct Answer is:C
To find the angle of projection of the particle, we can follow these steps:
Step 1: Identify the components of the velocity vector
The velocity vector is given as:
→v=6^i+2^jm/s
From this, we can identify the horizontal (x) and vertical (y) components of the velocity:
- vx=6m/s
- vy=2m/s
Step 2: Use the kinematic equation to find the initial vertical velocity
Since the particle is projected from a height of 0.4 m, we can use the kinematic equation:
v2y=u2y−2gh
Rearranging this gives:
u2y=v2y+2gh
Substituting the known values:
- vy=2m/s
- g=10m/s2
- h=0.4m
Calculating uy:
u2y=(2)2+2⋅10⋅0.4
u2y=4+8=12
uy=√12=2√3m/s
Step 3: Find the angle of projection
The angle of projection θ can be found using the tangent function:
tanθ=uyux
Substituting the values:
tanθ=2√36
Simplifying:
tanθ=√33
This implies:
θ=30∘
Final Answer
The angle of projection is 30∘.
---
The velocity vector is given as:
→v=6^i+2^jm/s
From this, we can identify the horizontal (x) and vertical (y) components of the velocity:
- vx=6m/s
- vy=2m/s
Since the particle is projected from a height of 0.4 m, we can use the kinematic equation:
v2y=u2y−2gh
Rearranging this gives:
u2y=v2y+2gh
Substituting the known values:
- vy=2m/s
- g=10m/s2
- h=0.4m
u2y=(2)2+2⋅10⋅0.4
u2y=4+8=12
uy=√12=2√3m/s
The angle of projection θ can be found using the tangent function:
tanθ=uyux
Substituting the values:
tanθ=2√36
Simplifying:
tanθ=√33
This implies:
θ=30∘
The angle of projection is 30∘.
Similar Questions
At a height 0.4m from the ground the velocity of a projectile in vector form is →v=(6ˆi+2ˆj)ms−1. The angle of projection is
View SolutionVelocity of a projectile at height 15m from ground is v=(20ˆi+10ˆj)m/s. Here ˆi is in horizontal direction and ˆj is vertically upwards. Then
Angle of projectile with ground is
View SolutionA particle is projected from ground with velocity 3ˆi+4ˆj m/s. Find range of the projectile :-
View SolutionVelocity of a projectile at height 15m from ground is v=(20ˆi+10ˆj)m/s. Here ˆi is in horizontal direction and ˆj is vertically upwards. Then
Horizontal range of the ground is …………m
View SolutionVelocity of a projectile at height 15m from ground is v=(20ˆi+10ˆj)m/s. Here ˆi is in horizontal direction and ˆj is vertically upwards. Then
Speed with which particle is projected from ground is……… m/s
View SolutionVelocity of a projectile at height 15m from ground is v=(20ˆi+10ˆj)m/s. Here ˆi is in horizontal direction and ˆj is vertically upwards. Then
Maximum height from a ground is ……..m
View SolutionA particle is projected from ground with velocity 40√2m/s at 45∘. At time t=2s
View SolutionAt a height of 15 m from ground velocity of a projectile is v=(10ˆi+10ˆj). Here ˆj is vertically upwards and ˆi is along horizontal direction then (g = 10 ms−1)
View SolutionA body is projected into air with a velocity (3i + 4j + 5k)m/s. Taking x-y plane as base and Z axis as vertical, the range of projectile (g =10m/s2)
View SolutionTwo graphs of the same projectile motion (in the xy-plane) projected from origin are shown. X-axis is along horizontal direction and y-axis is vertically upwards. Take g=10ms−2.
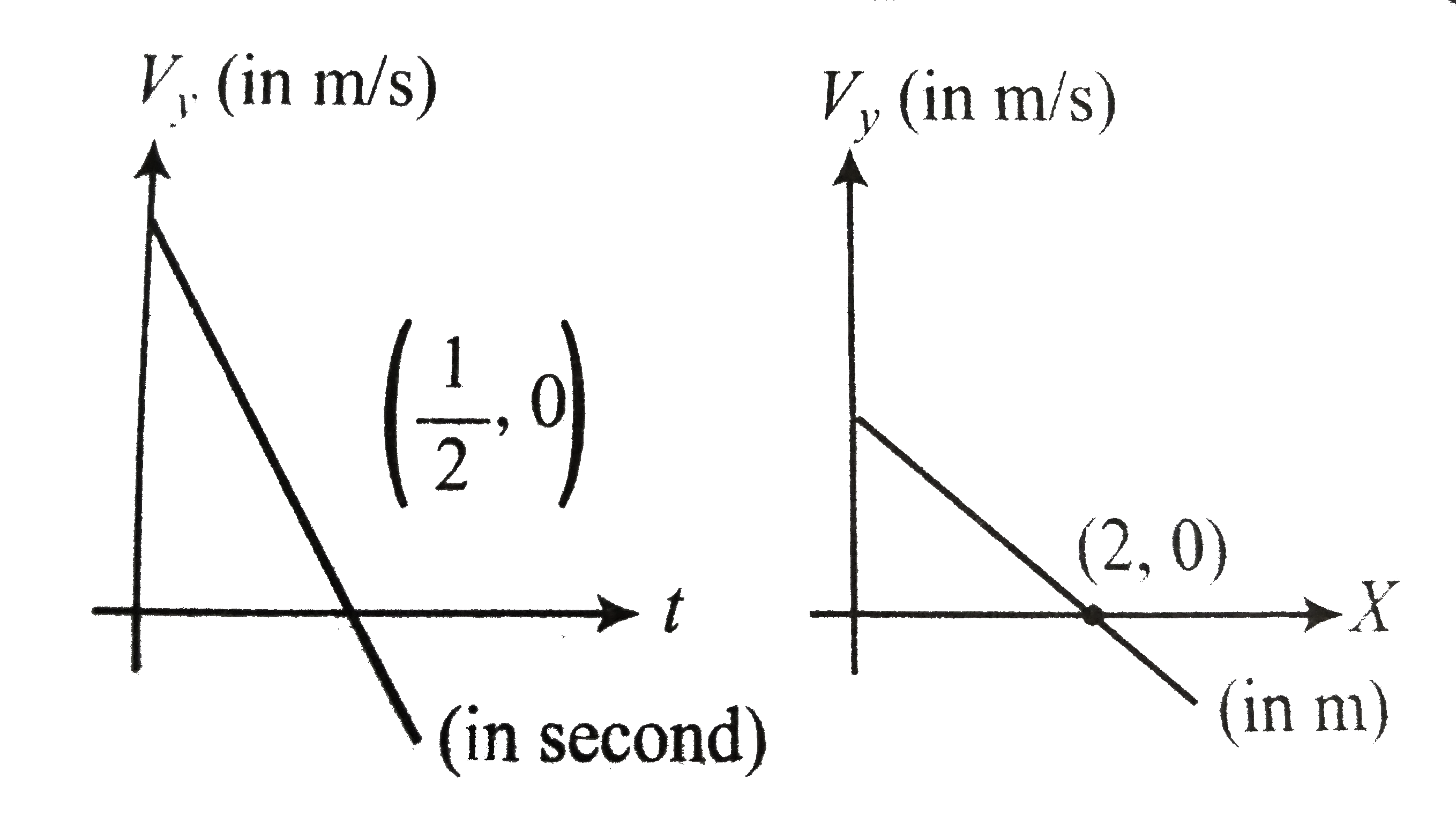 ,
,
The projection speed is :
View Solution
