If a ball strickes with a velocity u1 at the wall which itself is approaching it with a velocity u2 then find the velocity of the ball after collision with the wall.
To solve the problem of finding the velocity of the ball after it collides with a wall that is approaching it, we can follow these steps:
Step 1: Understand the scenario
We have a ball moving towards a wall with an initial velocity u1 while the wall is moving towards the ball with a velocity u2. We need to find the velocity of the ball after the collision.
Step 2: Define the velocities
- Let the velocity of the ball before the collision be u1 (towards the wall).
- Let the velocity of the wall be u2 (towards the ball).
Step 3: Consider the wall's mass
Assume the wall is very massive compared to the ball. This means that the wall will not change its velocity significantly due to the collision.
Step 4: Use the concept of relative velocity
In a collision, the relative velocity of approach is equal to the negative of the relative velocity of separation. This can be expressed as:
v1−v2=−(u1+u2)
where:
- v1 is the velocity of the ball after the collision,
- v2 is the velocity of the wall after the collision (which remains u2 since the wall is massive).
Step 5: Set up the equation
Since the wall's velocity remains u2 after the collision, we can substitute v2 into the equation:
v1−u2=−(u1+u2)
Step 6: Solve for v1
Rearranging the equation gives:
v1=−u1−u2+u2
This simplifies to:
v1=−u1+u2
Step 7: Conclusion
Thus, the velocity of the ball after the collision with the wall is:
v1=−u1+u2
We have a ball moving towards a wall with an initial velocity u1 while the wall is moving towards the ball with a velocity u2. We need to find the velocity of the ball after the collision.
- Let the velocity of the ball before the collision be u1 (towards the wall).
- Let the velocity of the wall be u2 (towards the ball).
Assume the wall is very massive compared to the ball. This means that the wall will not change its velocity significantly due to the collision.
In a collision, the relative velocity of approach is equal to the negative of the relative velocity of separation. This can be expressed as:
v1−v2=−(u1+u2)
where:
- v1 is the velocity of the ball after the collision,
- v2 is the velocity of the wall after the collision (which remains u2 since the wall is massive).
Since the wall's velocity remains u2 after the collision, we can substitute v2 into the equation:
v1−u2=−(u1+u2)
Rearranging the equation gives:
v1=−u1−u2+u2
This simplifies to:
v1=−u1+u2
Thus, the velocity of the ball after the collision with the wall is:
v1=−u1+u2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Solved Examples13videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.120videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
A ball of mass M/2 filled with a gas ( whose mass is M/2) is kept on a frictionless table . A bullet of mass m=M/4 and velocity v0ˆi penetrates the ball , and rests inside at t=0. Assume that the amount of gas emitted during the collision can be neglected. The compressed gas is emitted at a contant velocity v0/2 relative to the ball and at an even rate k ( k is a positive constant ) .
(a) What is the velocity of the ball after the collision with the bullet ?
(b) Find the velocity of the ball v(t) as a function of time. Assume that the emission of gas starts at t=0. What is the final velocity of the ball ?
 View Solution
View SolutionA small ball of mass m collides with as rough wal having coeficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves wilth angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.
 View Solution
View SolutionA ping-pong ball strikes a wall with a velocity of 10ms−1. If the collision is perfectly elastic, find the velocity if ball after impact
View SolutionA particle of mass m moves with velocity u1=20m/s towards a wall that is moving with velocity u2=5m/s. If the particle collides with the wall without losing its energy, find the speed of particle just after the collision.
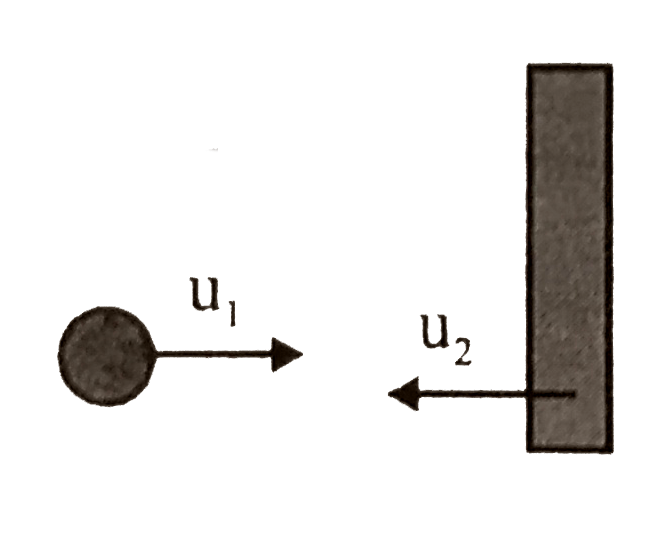 View Solution
View SolutionA ball collides elastically with a massive wall moving towards it with a velocity of v as shown. The collision occurs at a height of h above ground level and the velocity of the ball just before collision is 2v in horizontal direction. The distance between the foot of the wall and the point on the ground where the ball lands, at the instant the ball lands, will be :
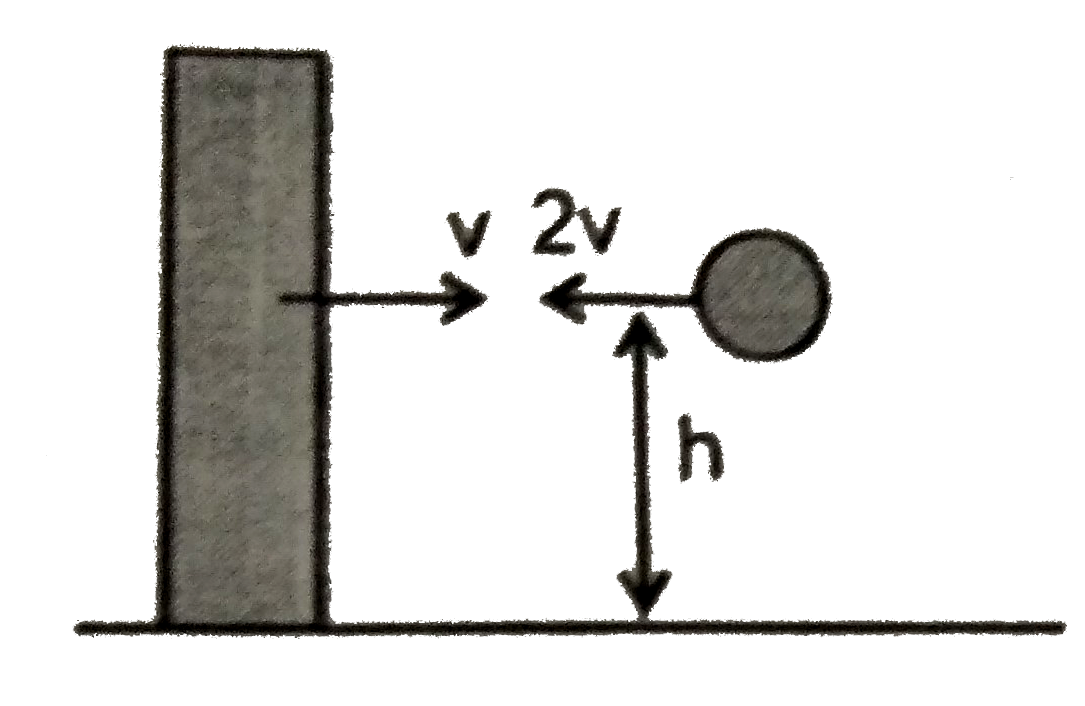 View Solution
View SolutionA ball of mass m moving with velocity v0 collides with a wall as shown in Fig. After impact it rebounds with a velocity' (v0)/2The component of impulse acting on the ball along the wall is
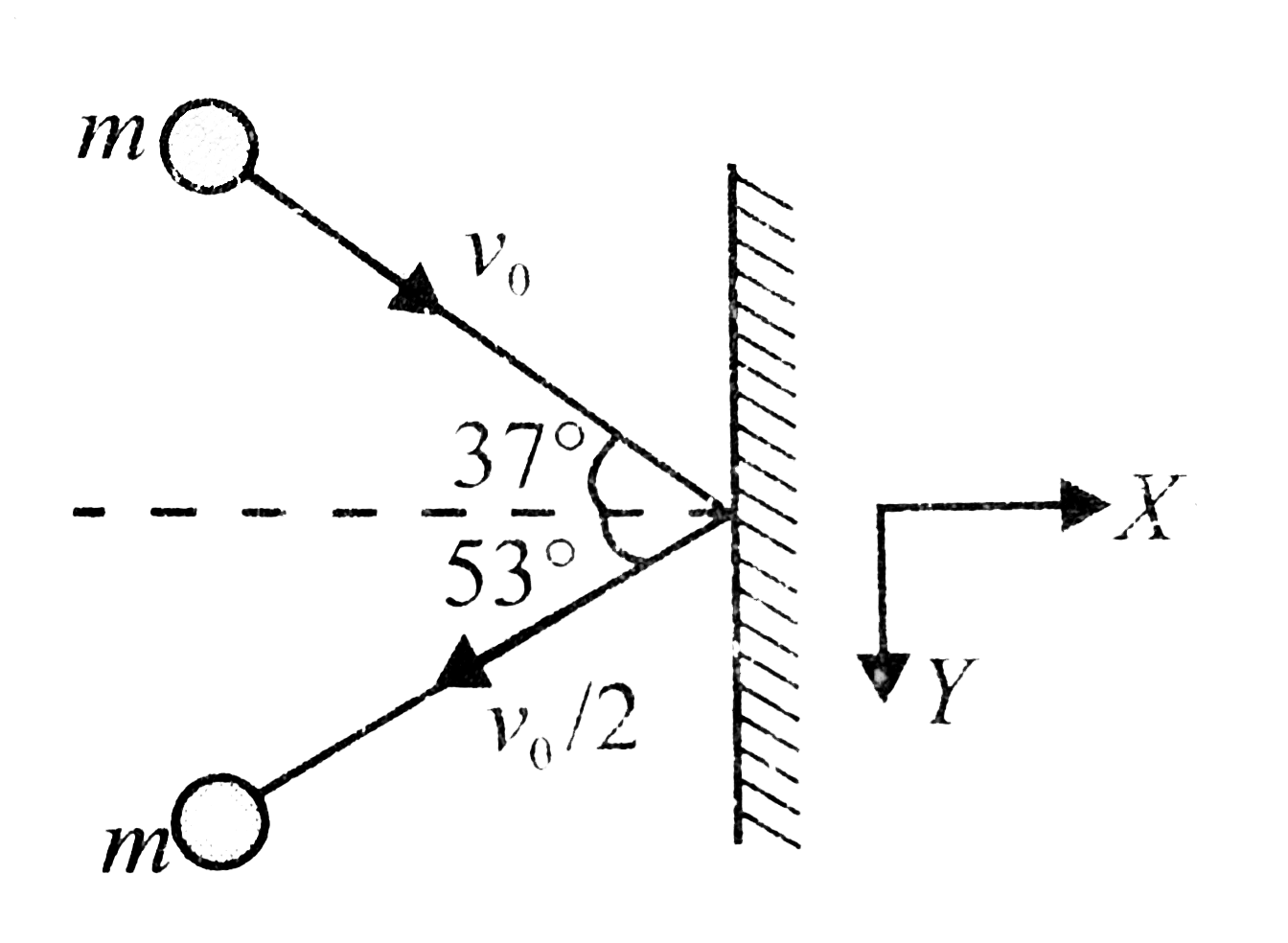 View Solution
View SolutionA small ball is projected horizontally between two large blocks. The ball is given a velocity Vms−1 and each of the large blocks move uniformly with a velocity of 2Vms−1. The ball collides elastically with the blocks. If the velocity of the blocks do not change due to the collision, then find out the velocity of the ball after the 2nd collision.
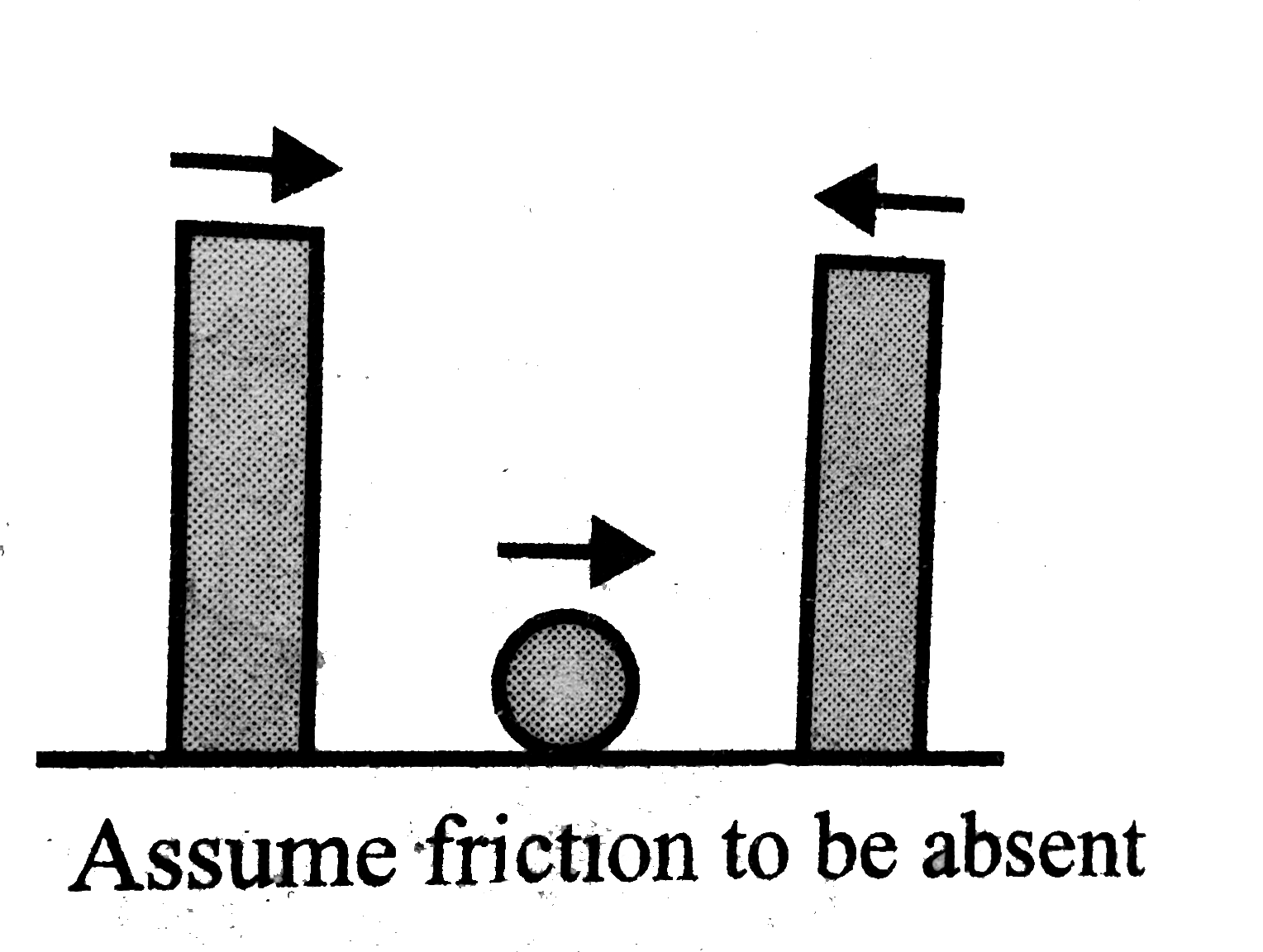 View Solution
View SolutionA glass ball collides with a smooth horizontal surface (xz plane) with a velocity V=ai−bj. If the coefficient of restitution of collision be e, the velocity of the ball just after the collision will be
View SolutionA ball of mass m moving with velocity u collides head-on which the second ball of mass m at rest. If the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
View SolutionA ball falls from a height such that it strikes the floor of lift at 10 m/s. If lift is moving in the upward direction with a velocity 1 m/s, then velocity with which the ball rebounds after elastic collision will be
View Solution

