A ball falls from a height such that it strikes the floor of lift at 10 m/s. If lift is moving in the upward direction with a velocity 1 m/s, then velocity with which the ball rebounds after elastic collision will be
11 m/s
12 m/s
13 m/s
9 m/s
The correct Answer is:B
To solve the problem, we need to analyze the motion of the ball and the lift during the collision.
Step 1: Understand the initial conditions.
- The ball is falling and strikes the floor of the lift with a velocity of 10 m/s downward.
- The lift is moving upward with a velocity of 1 m/s.
Step 2: Determine the relative velocity of approach.
- The relative velocity of the ball with respect to the lift just before the collision can be calculated as:
Relative velocity of approach=Velocity of ball+Velocity of lift=10m/s+1m/s=11m/s
(Note: Both velocities are in opposite directions, hence they are added.)
Step 3: Apply the principle of elastic collision.
- In an elastic collision, the relative velocity of separation after the collision is equal to the relative velocity of approach before the collision.
- Let v be the velocity of the ball after the collision. The lift continues to move upward at 1 m/s.
Step 4: Determine the relative velocity of separation.
- The relative velocity of separation can be expressed as:
Relative velocity of separation=Velocity of ball after collision−Velocity of lift=v−1m/s
Step 5: Set up the equation using the elastic collision condition.
- According to the principle of elastic collision:
Relative velocity of separation=Relative velocity of approach
Thus, we have:
v−1=11
Step 6: Solve for v.
- Rearranging the equation gives:
v=11+1=12m/s
Conclusion:
- The velocity with which the ball rebounds after the elastic collision is 12 m/s upward.
---
- The ball is falling and strikes the floor of the lift with a velocity of 10 m/s downward.
- The lift is moving upward with a velocity of 1 m/s.
- The relative velocity of the ball with respect to the lift just before the collision can be calculated as:
Relative velocity of approach=Velocity of ball+Velocity of lift=10m/s+1m/s=11m/s
(Note: Both velocities are in opposite directions, hence they are added.)
- In an elastic collision, the relative velocity of separation after the collision is equal to the relative velocity of approach before the collision.
- Let v be the velocity of the ball after the collision. The lift continues to move upward at 1 m/s.
- The relative velocity of separation can be expressed as:
Relative velocity of separation=Velocity of ball after collision−Velocity of lift=v−1m/s
- According to the principle of elastic collision:
Relative velocity of separation=Relative velocity of approach
Thus, we have:
v−1=11
- Rearranging the equation gives:
v=11+1=12m/s
- The velocity with which the ball rebounds after the elastic collision is 12 m/s upward.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:Assignment (SECTION - A)
Explore 64 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:Assignment (SECTION - B)
Explore 35 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:SECTION-J (AAKASH CHALLENGERS QUESTIONS)
Explore 14 Videos
- WAVESBook:AAKASH INSTITUTE ENGLISHChapter:WAVESExercise:ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
Explore 12 Videos
Similar Questions
A ball after falling a distance of 5 meter rest hits elastically the floor of a lift and rebounds. At the time of impact the lift was moving up with a velocity of 1m/sec. The velocity with which the ball rebounds just after impact is : (g=10m/sec2)
View SolutionTwo elastic bodies P and Q having equal mases are moving along the same line with velocities of 16 m/s and 10 m/s respectively. Their velocities after the elastic collision will be in m/s :
View SolutionA ball is thrown vertically upwards from the top of tower of height h with velocity v . The ball strikes the ground after time.
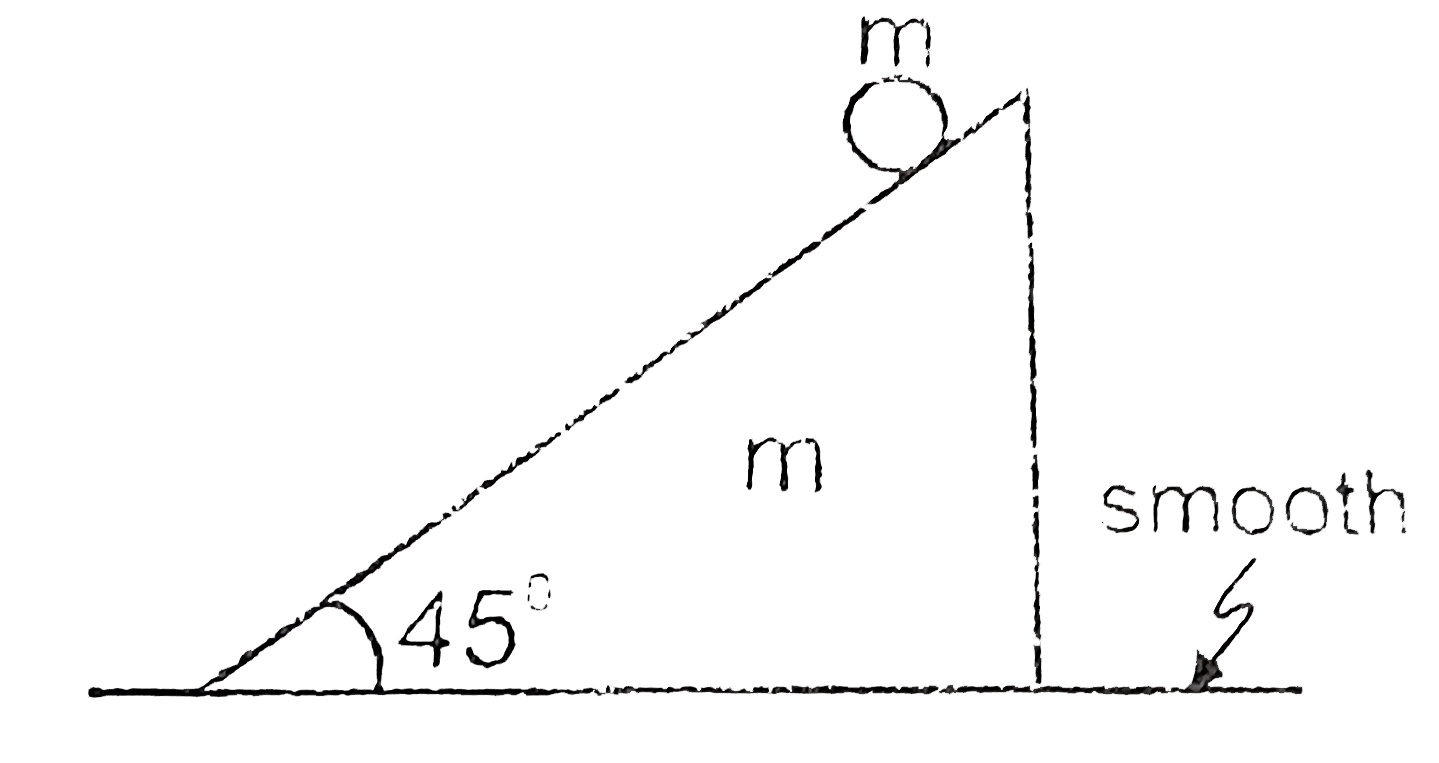
View SolutionA ball of mass 'm is released from the top of a smooth movable wedge of mass 'm'. When the ball collides with the floor, velocity is 'v'. Then the maximum height attained by the ball after an elastic collision with the floor is : (Nelect any edge at the lower end of the wedge)
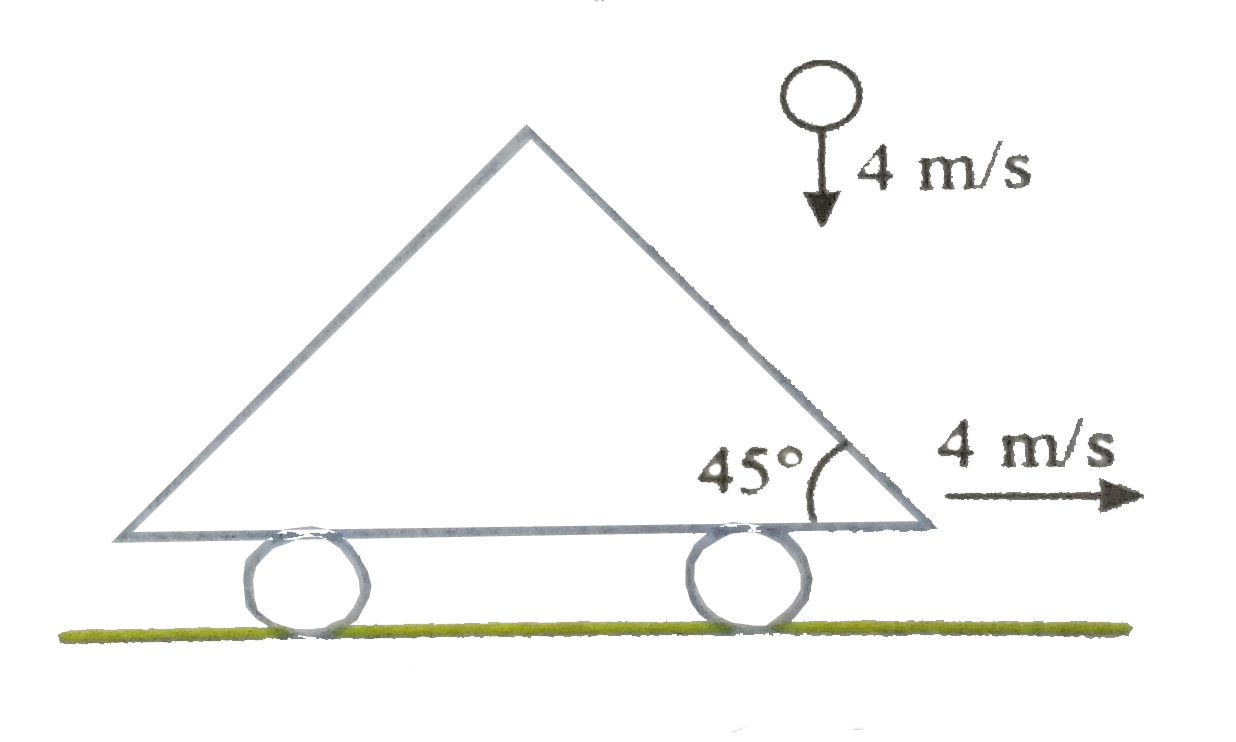
View SolutionA small ball falling vertically downward with constant velocity 4m/s strikes elastically a massive inclined cart moving with velocity 4m/s horizontally as shown. The velocity of the rebound of the ball is
View SolutionTwo balls of masses m and 2m moving in opposite directions collide head on elastically with velocities v and 2v. Find their velocities after collision.
View SolutionTwo balls of masses m and 2m moving in opposite directions collide head on elastically with velocities v and 2v. Find their velocities after collision.
View SolutionA ball is thrown vertically upward with a velocity of 20 m/s. Calculate the maximum height attain by the ball.
View SolutionAn elevator without a ceiling is ascending up with an acceleration of 5ms−2. A boy on the elevator shoots a ball in vertical upward direction from a height of 2 m above the floor of elevator. At this instant the elevator is moving up with a velocity of 10ms−1 and floor of the elevator is at a height of 50 m from the ground. The initial speed of the ball is 15ms−1 with respect to the elevator. Consider the duration for which the ball strikes the floor of elevator in answering following questions. (g=10ms−2)
1. The time in which the ball strikes the floor of elevator is given by
View SolutionA coin is released inside a lift at a height of 2m from the floor of the lift. The height of the lift is 10 m. The lift is moving with an acceleration of 9m/s2downwards. The time after which the coin will strike with the lift is : (g=10m/s2)
View Solution