Thre identical masses are kept at the corners of an equilateral triangle ABC. A moves towards B with a velocity V, B moves towards C with velocity V, and C moves towards A with same velocity V. Then the velocity of centre of mass of the system of particles is
V
zero
3V
V3
The correct Answer is:B
To solve the problem, we need to determine the velocity of the center of mass of a system of three identical masses located at the corners of an equilateral triangle, each moving towards the next mass with the same velocity V.
1. Identify the Masses and Their Positions:
- Let the three identical masses be m located at points A, B, and C of the equilateral triangle.
2. Define the Velocities:
- Mass A moves towards mass B with velocity V.
- Mass B moves towards mass C with velocity V.
- Mass C moves towards mass A with velocity V.
3. Determine the Center of Mass:
- The center of mass →Rcm of a system of particles is given by the formula:
→Rcm=1M∑imi→ri
where M is the total mass and →ri are the position vectors of the masses.
4. Calculate the Total Mass:
- The total mass M of the system is:
M=m+m+m=3m
5. Express the Velocities as Vectors:
- Let →VA, →VB, and →VC be the velocity vectors of masses A, B, and C respectively. Each of these vectors has a magnitude of V.
6. Sum of the Velocity Vectors:
- The velocity vectors can be expressed as:
→VA+→VB+→VC
- Since the masses are moving towards each other in a symmetrical manner, the sum of these vectors will yield a null vector:
→VA+→VB+→VC=0
7. Calculate the Velocity of the Center of Mass:
- The velocity of the center of mass →Vcm is given by:
→Vcm=1M(m→VA+m→VB+m→VC)=13m(m→VA+m→VB+m→VC)
- Since →VA+→VB+→VC=0, we have:
→Vcm=13m(0)=0
Conclusion:
The velocity of the center of mass of the system of particles is 0.
- Let the three identical masses be m located at points A, B, and C of the equilateral triangle.
- Mass A moves towards mass B with velocity V.
- Mass B moves towards mass C with velocity V.
- Mass C moves towards mass A with velocity V.
- The center of mass →Rcm of a system of particles is given by the formula:
→Rcm=1M∑imi→ri
where M is the total mass and →ri are the position vectors of the masses.
- The total mass M of the system is:
M=m+m+m=3m
- Let →VA, →VB, and →VC be the velocity vectors of masses A, B, and C respectively. Each of these vectors has a magnitude of V.
- The velocity vectors can be expressed as:
→VA+→VB+→VC
- Since the masses are moving towards each other in a symmetrical manner, the sum of these vectors will yield a null vector:
→VA+→VB+→VC=0
- The velocity of the center of mass →Vcm is given by:
→Vcm=1M(m→VA+m→VB+m→VC)=13m(m→VA+m→VB+m→VC)
- Since →VA+→VB+→VC=0, we have:
→Vcm=13m(0)=0
The velocity of the center of mass of the system of particles is 0.
Similar Questions
Knowledge Check
A particle moves in the direction of east for 2s with velocity of 15m/s .Then it moves towards north for 8s with a velocity of 5m/s . The average velocity of the particle is (in m/s)
A1 m/sB5 m/sC7 m/sD10 m/s
A person moves with a velocity v towards a plane mirror. With what velocity does his image move towards him ?
View Solution(a) Show that the velocity of the centre of mass of a moving isolated system remains constant.
View SolutionTwo partticles A and B intially at rest move towards each other under a mutual force of attraction. The instant at which velocity of A is 4v and velocity of B is 2v, the velocity of centre of mass of the system at that instant will be
View SolutionOut of the two cars A and B car A is moving towards east with velocity of 10 m/s whereas B is moving towards north with a velocity 20 m/s, then velocity of A w.r.t B is ( nearly )
View SolutionA particle moves in the direction of east for 2s with velocity of 15ms−1. Then it moves towards north for 8s with a a velocity of 5ms−1. The average velocity of the particle is
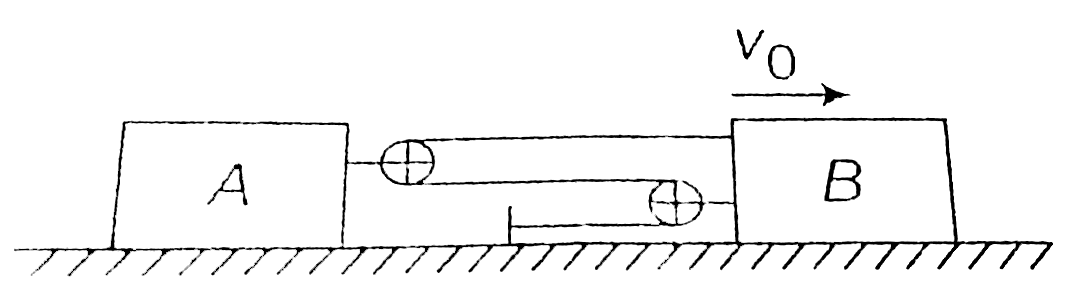
View SolutionBlock B moves to the right with a constant velocity v0. The velocity of body a relative to b is
View SolutionLet there are three equal masses situated at the vertices of an equilateral triangle, as shown in Fig. Now particle A starts with a velocity v1 towards line AB, particle B starts with the velocity v2, towards line BC and particle C starts with velocity v3 towards line CA. Find the displacement of the centre of mass of the three particles A,B and C after time t. What would it be if v1=v2=v3?
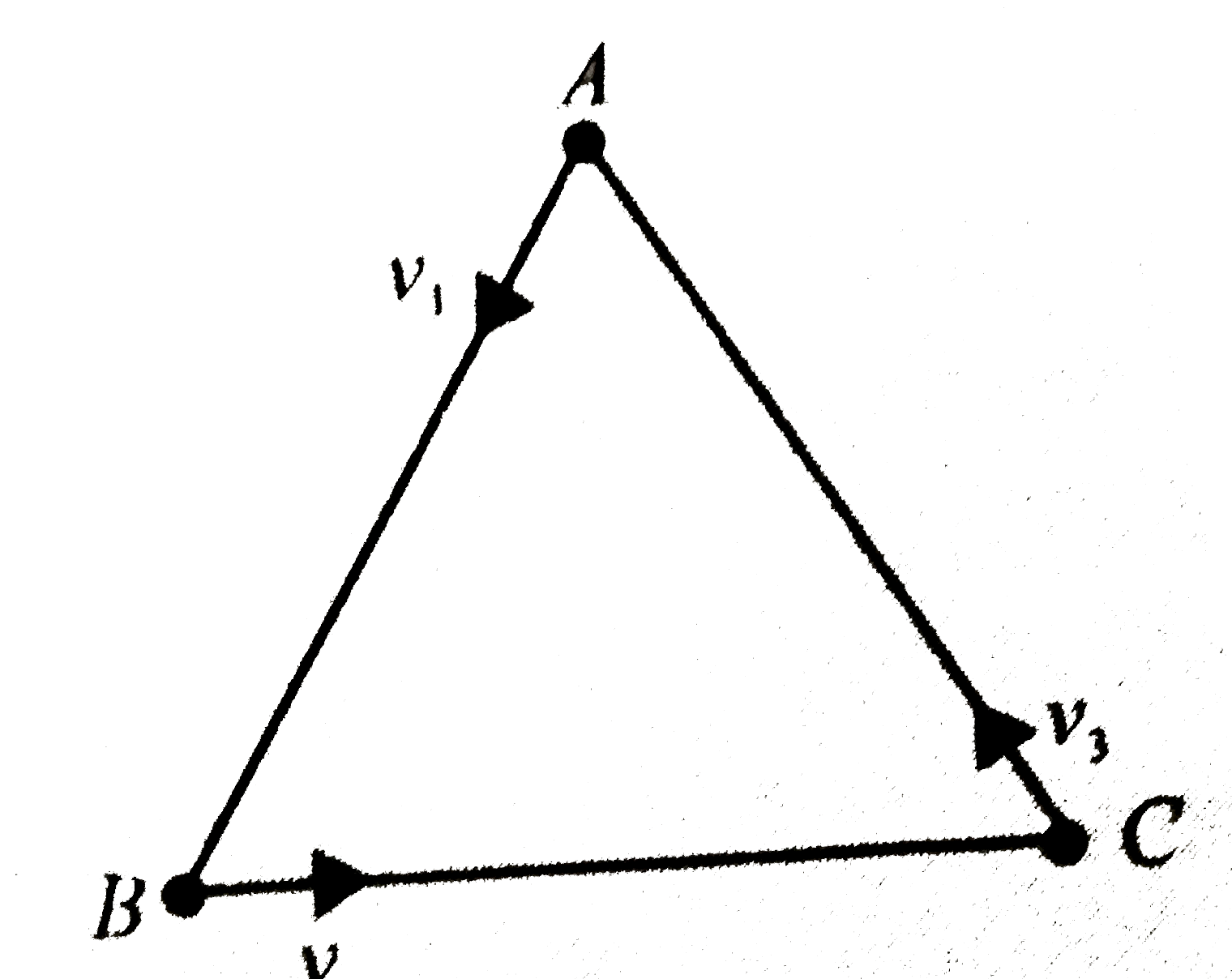
View Solution
