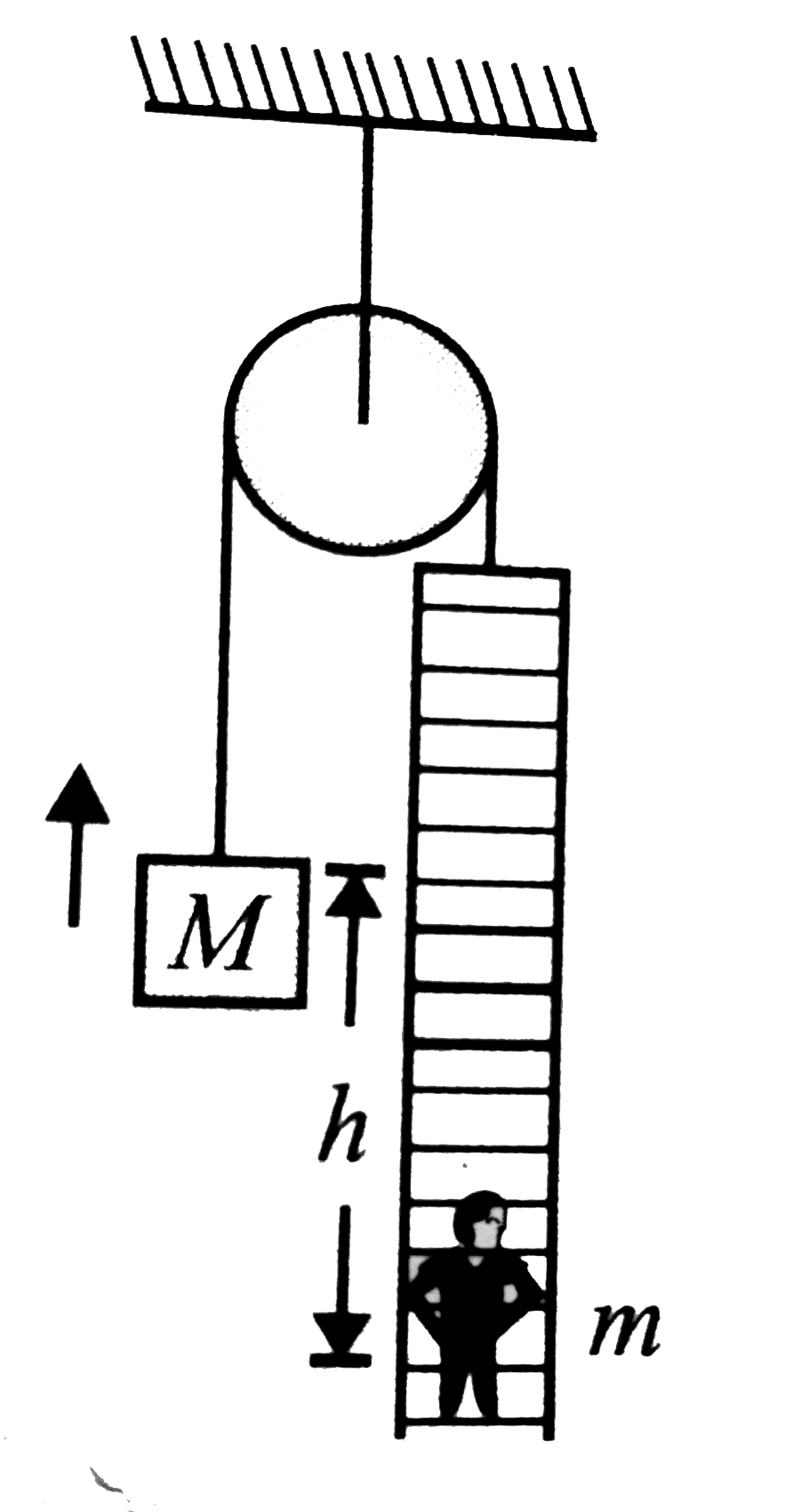
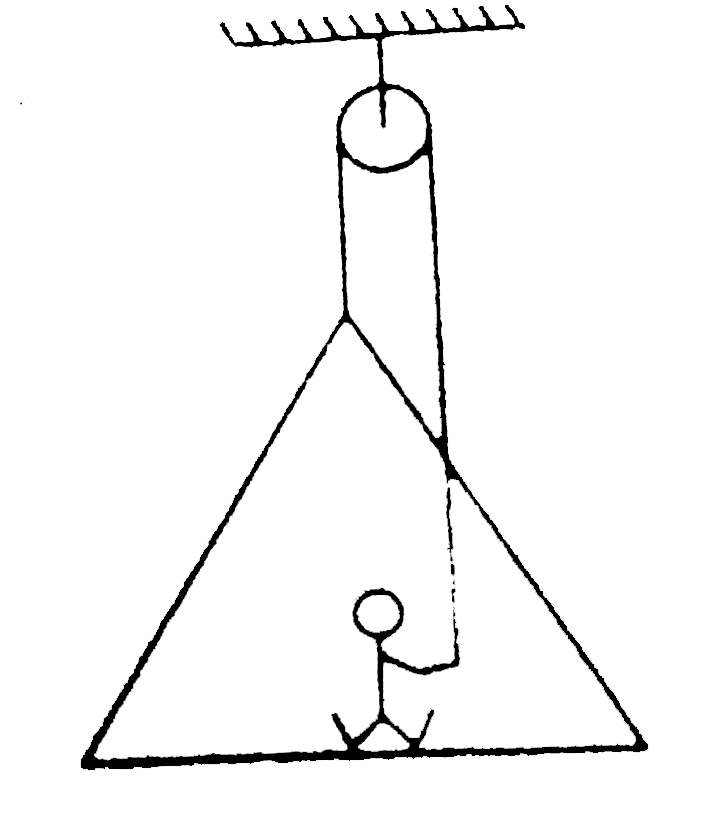
A stationary light, smooth pulley can rotate without friction about a fixed horizontal axis. A light rope passes over the pulley. One end of the rope supports a ladder with man and the other end supports a counterweight of mass M. Mass of the man is m. initially, the centre of mass of the counterweight is at a height h from that of man as shown in Fig.
If the man starts to climb up the ladder slowly, calculate work done by him to reach his centre of mass in level with that of the counterweight.
The correct Answer is:W=MmghM−m
Mass of ladder =M−m, because net mass on both sides of string is same. Let in the given process, block M rises by height y, then ladder will come down by distance y and when man comes in the level of M, then height raised by man w.r.t ground will be h+y.
Now cenre of mass (man+ladder) system will be raised by y , then

y=m(h+y)+(M−m)(−y)2(M−m)
Now work done by man
W=total change in potential energy of system
⇒W=Mgy+mg(h+y)−(M−m)gy
Put the values of y and solve to get W=MmghM−m
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Single Correct141videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct25videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.324videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
A stationary pulley carries a rope whose one end supports a ladder with a man and the other end the counterweight of mass M. The man of mass m climbs up a distance l with respect to the ladder and then stops. Neglecting the mass of the rope and the friction in the pulley axle, find the displacement I of the centre of inertia of this system.
View SolutionA man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon
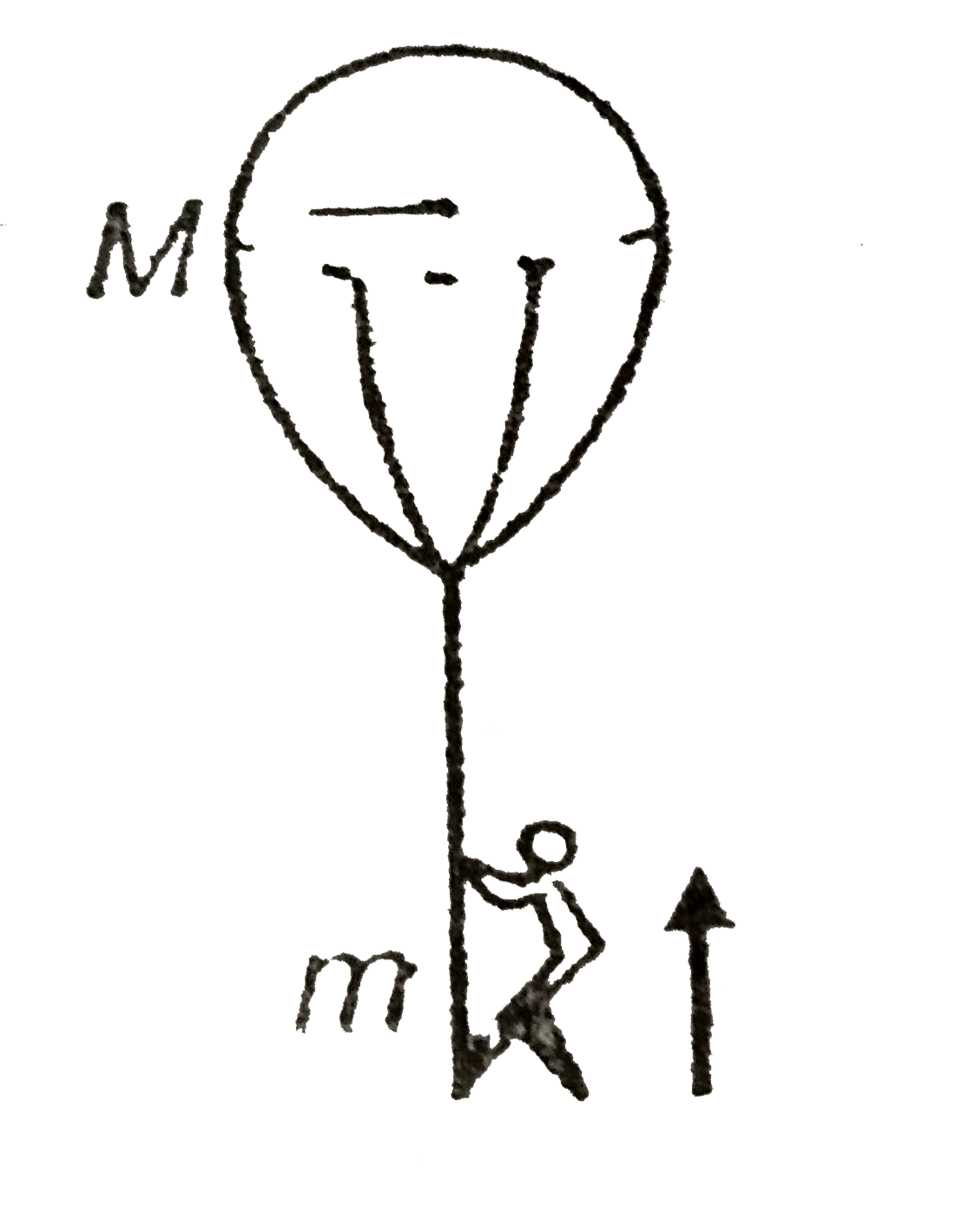 View Solution
View SolutionA man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon
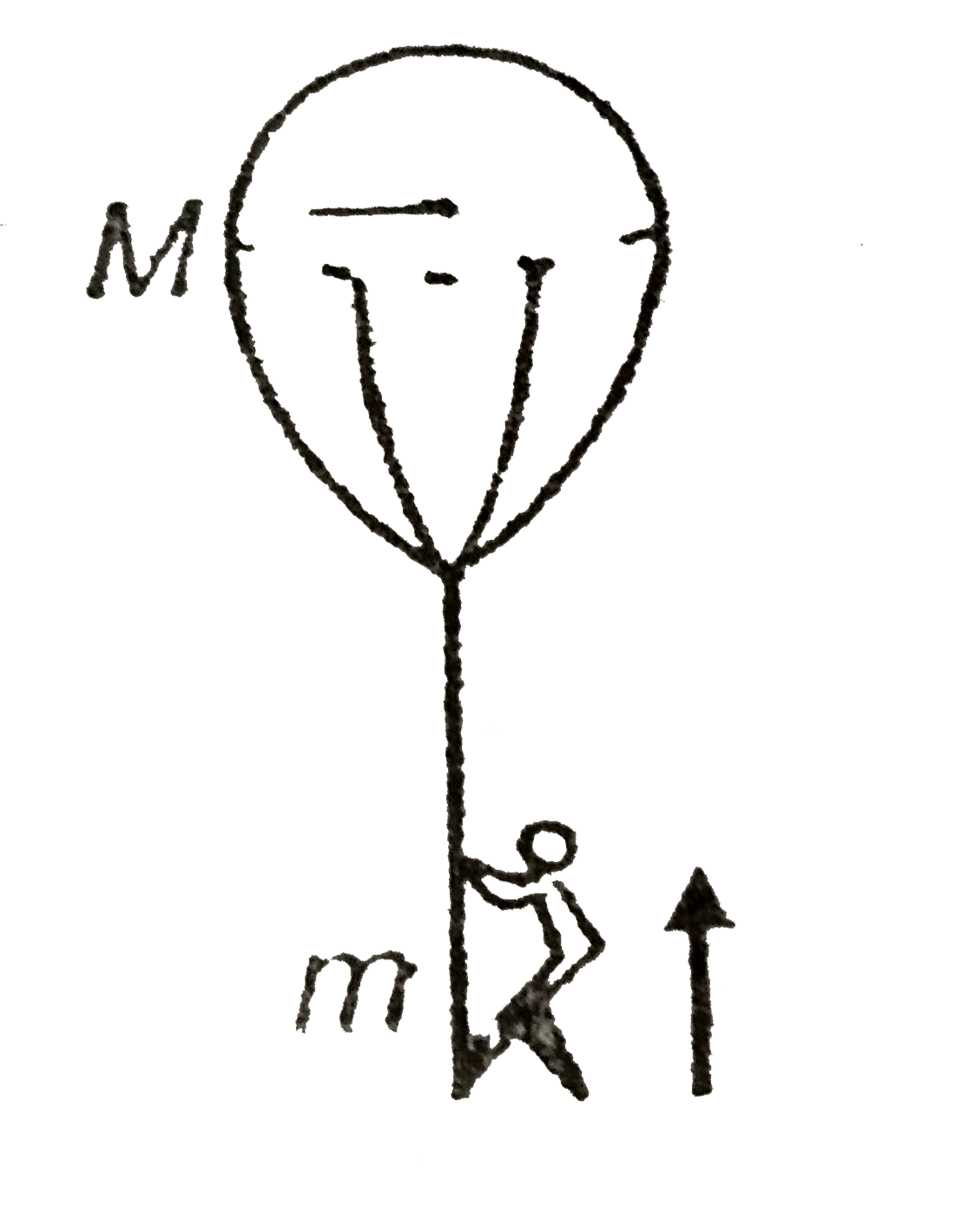 View Solution
View SolutionA man of mass m is standing on a stationary flat car of mass M. The car can move without friction along horizontal rails. The man starts walking with velocity v relative to the car. Work done by him
View SolutionA man of mass m stands on a frame of mass M. He pulls on a light rope, which passes over a pulley. The other end of the rope is attached to the frame. For the system to be in equilibrium, what force must the man exert on the rope?
 View Solution
View SolutionIn fig., the mass of the man is M. Calculate the mass of the man as registered by weighing machine. Assume weighing machine, man, and wedge all are stationary.
 View Solution
View SolutionA rope thrown over a pulley has a ladder with a man of mass m on one of its ends and a counter balancing mass M on its other end. The man climbs with a velocity vr relative to ladder. Ignoring the masses of the pulley and the rope as well as the friction on the pulley axis, the velocity of the centre of mass of this system is:
View SolutionA Monkey is Climbing on a Rope that Goes Over a Smooth Light Pulley and Supports a Block of Equal Mass at the Other End in the Following
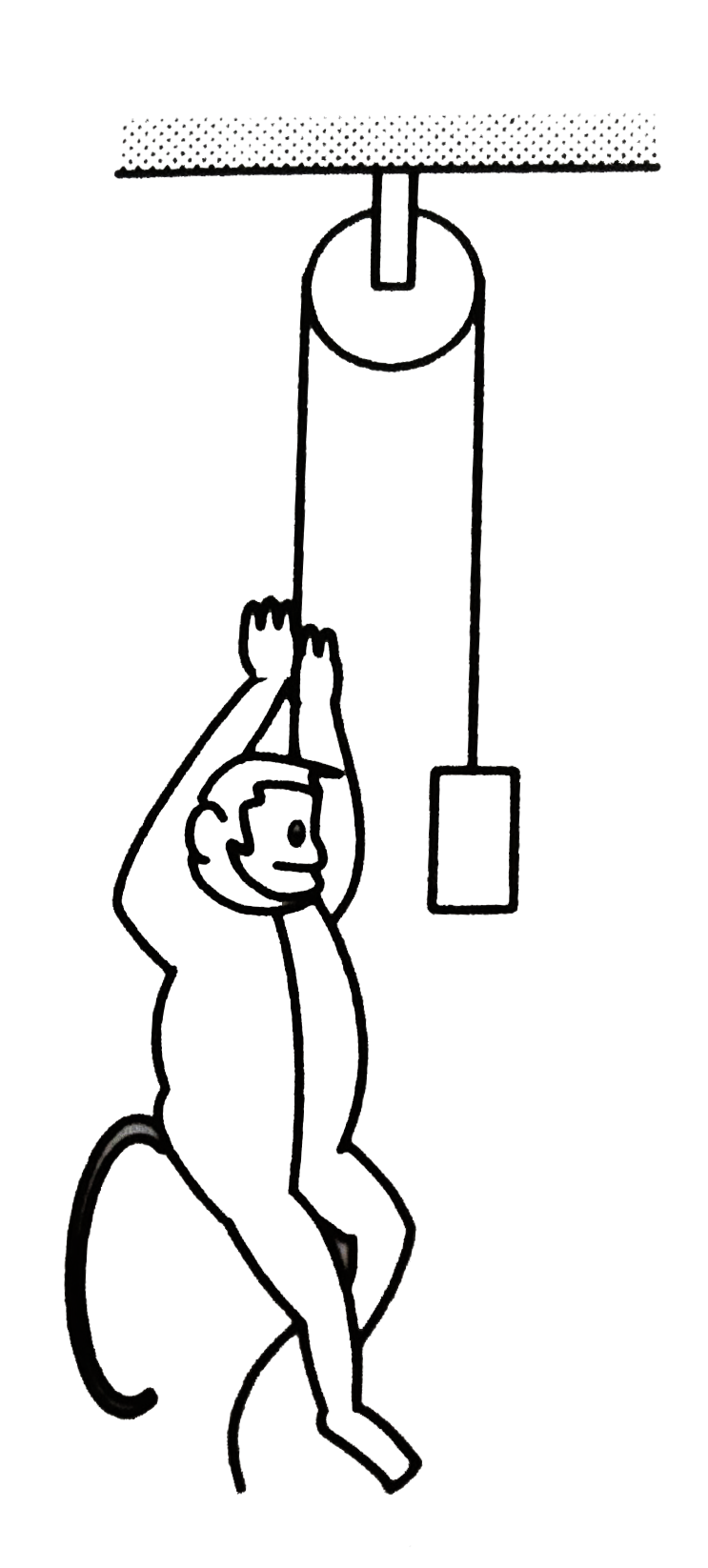 View Solution
View SolutionA mam of mass 50 g stands on a frame of mass 30 g. He pulls on a light rope which passes over a pulley. The other end of the rope is attached to the frame. For the system to be in equilibrium what force man must exert on the rope?
 View Solution
View SolutionA light rope is passed over a pulley such that at its one end a block is attached , and on the other end a boy is climbing up with acceleration g2 relative to rope. Mass of the block is 30 kg and that of the boy is 40 kg. Find the tension and acceleration of the rope .
View Solution

