Two pendulums each of length l are initially situated as shown in Fig. The first pendulum is released and strikes the second. Assume that the collision is completely inelastic and neglect the mass of the string and any frictional effects. How high does the centre of mass rise after the collision?

d[m1(m1+m2)]2
d[m1(m1+m2)]
d[(m1+m2)m2]2
[m2(m1+m2)]2
The correct Answer is:A
Applying the law of conservatioin of momentum
m1v1=(m1+m2)V …………i
where v1=√2gd is the velocity with which m1 collides with m2 therefore
V=m1(m1+m2)√2gd
Now, let the centre of mass rise through a height h after collision. In this case, the kinetic enerty of m1+m2 system is converted into potential energy at maximum height h
⇒12(m1+m2)V2=(m1+m2)gh
⇒12(m1+m2){m1m1+m2}22gh=(m1+m2)gh
⇒h=d{m1m1+m2}2
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
Two balls having masses m and 2m are fastened to two light strings of same length shown in the figure. The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a). Find velocities of the balls just after their collision. (b). How high will the balls rise after the collision.

View SolutionA ball of mass m moving horizontally at a speed v collides with the bob of a simple pendulum at rest. The mass of the bob is also m. If the collision is perfectly elastic and both balls sticks, the height to which the two balls rise after the collision will be given by:
View Solution
Knowledge Check
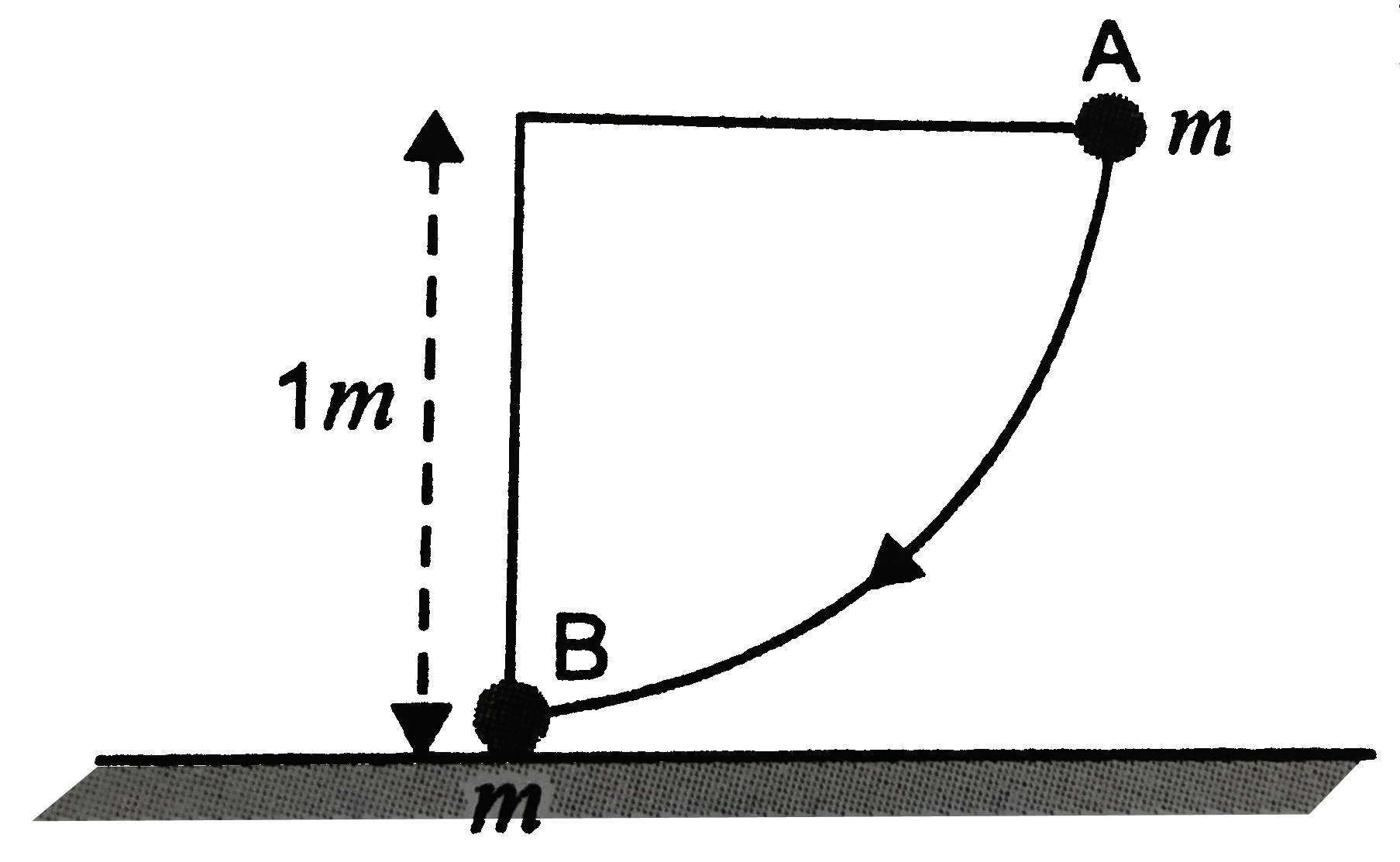
The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
If the length of the pendulum is 1m, calculate
(a) the height to which bob A will rise after collision.
(b) the speed with which bob B starts moving.
Neglect the size of the bobs and assume the collision to be elastic.
 A4.47ms−1B5.47ms−1C6.47ms−1D3.47ms−1
A4.47ms−1B5.47ms−1C6.47ms−1D3.47ms−1
Two massless string of length 5 m hang from the ceiling very near to each other as shown in the figure. Two balls A and B of masses 0.25kg and 0.5kg are attached to the string. The ball A is released from rest at a height 0.45m as shown in the figure. The collision between two balls is completely elastic. Immediately after the collision, the kinetic energy of ball B is 1J The velocity of ball A just after the collision is
Q01.png)
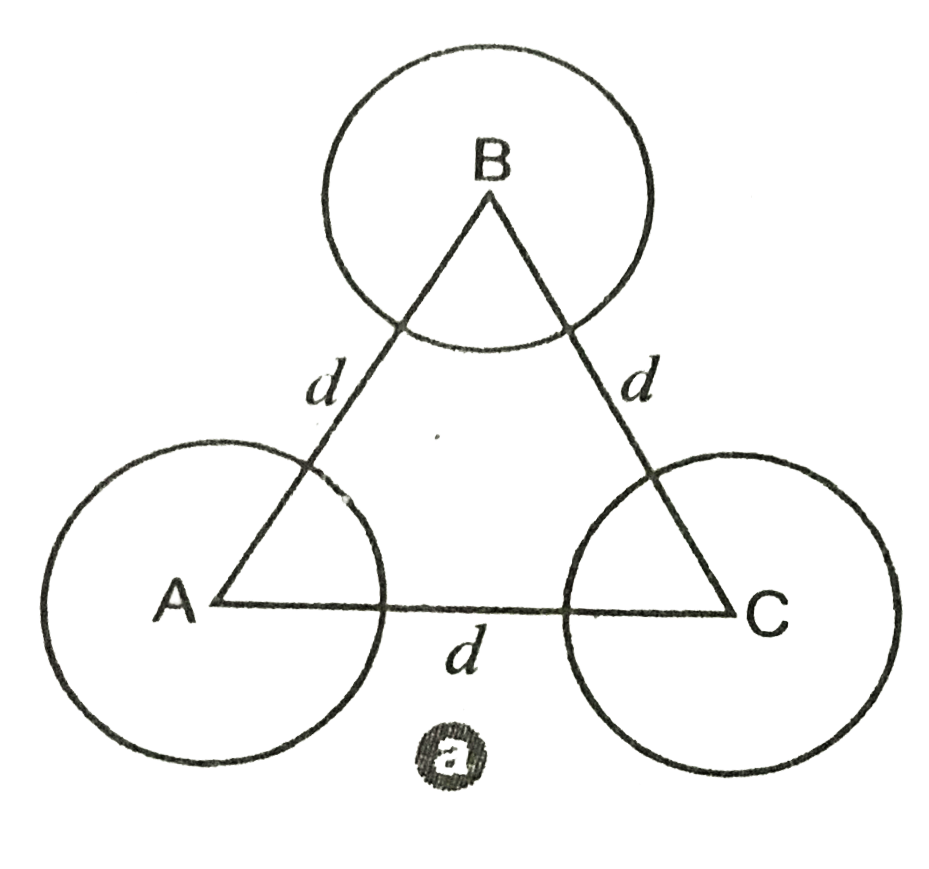
View SolutionThree solid spheres each of mass m and radius R are released from the position shown in Fig. What is the speed of any one sphere at the time of collision?
View SolutionA 2kg mass is attached to a spring of force constant 600N/m and rests on a smooth horizontal surface. A second mass of 1kg slides along the surface toward the first at 6m/s.
(a) Find the amplitude of oscillation if the masses make a perfectly inelastic collision and remain together on the spring. what is the period of oscillation ?
(b) Find the amplitude and period of oscillation if the collision is perfectly elastic.
( c) For each case , write down the position x as a function of time t for the mass attached to the spring, assuming that the collision occurs at time t=0. What is the impulse given to the 2kg mass in each case ?
View SolutionThe bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
If the length of the pendulum is 1m, calculate
(a) the height to which bob A will rise after collision.
(b) the speed with which bob B starts moving.
Neglect the size of the bobs and assume the collision to be elastic.

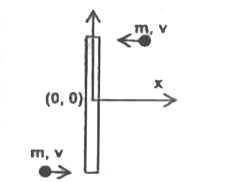
View SolutionA rigid uniform rod of mass M and length L is placed along the Y-axis on a smooth horizontal surface with its centre at the origin. Two particles , each of mas m(=M/12) hits simultaneously , at the two ends with equal speed v as shown in the figure. The collision is completely inelastic.
(i) Find the angular velocity of the system after the collision.
(ii) Two particles of mass 2m and m are placed respectively at ( L/2,0) and (−L/2,0). Calculate the time when the rod hits these particles.
View SolutionThe period P of a simple pendulum is the time for one complete swing. How does P depend on the mass m of the bob, the length l of the string, and the acceleration due to gravity g?
View SolutionA block of mass m and a pan of equal mass are connected by a string going over a smooth light pulley as shown in figure. Initially the system is at rest when a particle of mass m falls on the pan and sticks to it. If the particle strikes the pan with a speed v find the speed with which the system moves just after the collision.
View Solution
