A canon shell moving along a straight line bursts into two parts. Just after the burst one part moves with momentum 20Ns making an angle 30∘ with the original line of motion. The minimum momentum of the other part of shell just after the burst is
0NS
5Ns
10Ns
17.32Ns
The correct Answer is:C
To solve the problem, we will use the principle of conservation of momentum. Here are the steps to find the minimum momentum of the second part of the shell after the burst.
1. Understanding the Problem:
We have a cannon shell that bursts into two parts. One part has a momentum of P1=20N s at an angle of 30∘ to the original line of motion. We need to find the minimum momentum of the second part P2.
2. Setting Up the Coordinate System:
Let's define the original direction of motion as the x-axis. After the burst, the momentum of the first part can be broken down into its components:
- P1x=P1cos(30∘)
- P1y=P1sin(30∘)
3. Calculating the Components of P1:
- P1x=20cos(30∘)=20×√32=10√3N s
- P1y=20sin(30∘)=20×12=10N s
4. Applying Conservation of Momentum:
According to the conservation of momentum, the total momentum before the burst must equal the total momentum after the burst. Since the initial momentum was entirely in the x-direction, we have:
- In the x-direction:
P1x+P2x=20N s
- In the y-direction:
P1y+P2y=0(since there was no initial y-component)
5. Setting Up the Equations:
From the x-direction:
10√3+P2x=20
Therefore,
P2x=20−10√3
From the y-direction:
10+P2y=0
Therefore,
P2y=−10
6. Calculating the Magnitude of P2:
The total momentum P2 can be calculated using the Pythagorean theorem:
P2=√P22x+P22y
Substituting the values:
P2=√(20−10√3)2+(−10)2
7. Simplifying the Expression:
Calculate (20−10√3)2:
=400−400√3+300=700−400√3
Now, calculate P2:
P2=√700−400√3+100=√800−400√3
8. Finding the Minimum Value:
To find the minimum momentum of P2, we need to maximize P1. The maximum value of P1 occurs when sin(θ)=1 (i.e., θ=90∘), which gives:
P1=10N s
Thus, the minimum momentum of the other part is P2=10N s.
Final Answer:
The minimum momentum of the other part of the shell just after the burst is 10N s.
We have a cannon shell that bursts into two parts. One part has a momentum of P1=20N s at an angle of 30∘ to the original line of motion. We need to find the minimum momentum of the second part P2.
Let's define the original direction of motion as the x-axis. After the burst, the momentum of the first part can be broken down into its components:
- P1x=P1cos(30∘)
- P1y=P1sin(30∘)
- P1x=20cos(30∘)=20×√32=10√3N s
- P1y=20sin(30∘)=20×12=10N s
According to the conservation of momentum, the total momentum before the burst must equal the total momentum after the burst. Since the initial momentum was entirely in the x-direction, we have:
- In the x-direction:
P1x+P2x=20N s
- In the y-direction:
P1y+P2y=0(since there was no initial y-component)
From the x-direction:
10√3+P2x=20
Therefore,
P2x=20−10√3
10+P2y=0
Therefore,
P2y=−10
The total momentum P2 can be calculated using the Pythagorean theorem:
P2=√P22x+P22y
Substituting the values:
P2=√(20−10√3)2+(−10)2
Calculate (20−10√3)2:
=400−400√3+300=700−400√3
Now, calculate P2:
P2=√700−400√3+100=√800−400√3
To find the minimum momentum of P2, we need to maximize P1. The maximum value of P1 occurs when sin(θ)=1 (i.e., θ=90∘), which gives:
P1=10N s
Thus, the minimum momentum of the other part is P2=10N s.
The minimum momentum of the other part of the shell just after the burst is 10N s.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A ball moving with a speed of 9ms−1 strikes an identical stationary ball such that after the collision the direction of each ball makes an angle of 30∘ with the original line of motion. The speeds of two balls after the collision is
View SolutionA particle P is moving along a straight line as shown in the figure. During the motion of the particle from A to B the angular momentum of the particle about O
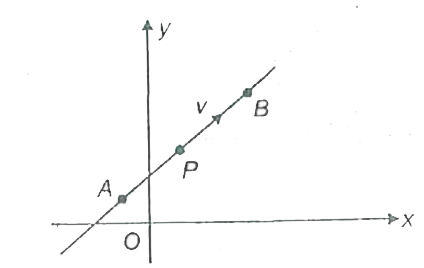
View Solution
Knowledge Check
A ball , moving with a speed of 10√3m/s , strikes an identical stationary ball such that after the collision , the direction of each ball makes an angle of 30∘with the original line of motion. The speeds of two balla after the collision are , respectively.
A3ms−1,3ms−1B3√3ms−1,3√3ms−1C3√3ms−1,3ms−1D3ms−1,3√3ms−1
A billiard ball moving at a speed of 6.6 ms–1 strikes an identical stationary ball a glancingblow. After the collision, one ball is found to be moving at a speed of 3.3, ms–1 in a direction making an angle of 60º with the original line of motion. The velocity of the other ball is
View SolutionA particle starts moving along a straight line path with velocity 10m/s. After 5s the distance of the particle from the starting point is 50m. Which of the following statements about the nature of motion of the particle are correct?
View SolutionA particle is moving along a straight line parallel to x-axis with constant velocity. Find angular momentum about the origin in vector form :

View SolutionA body moves a distance of 5 m along a straight line under the action of a force 10 N. If the work done is 25√3 joule, the angle which the force makes with the direction of motion of the body is
View SolutionA projectile is moving at 20ms−1 at its highest point where it breaks into equal parts due to an internal explosion. Just after explosion, one part moves vertically up at 30ms−1 with respect to the ground. Then the other part will move at :
View SolutionA particle moves along a straight line path. After some time it comes to rest. The motion is with constant acceleration whose direction with respect to the direction of velocity is :
View SolutionA particle moves along a straight line path. After some time it comes to rest. The motion is with constant acceleration whose direction with respect to the direction of velocity is :
View Solution
