A bag of mass M hangs by a long massless rope. A bullet of mass in, moving horizontally with velocity u, is caught in the bag. Then for the combined (bag + bullet) system, just after collision
momentum is muM/(M+m)
kinetic energy is mu2/2
momentum is mu(M+m)/M
kinetic energy is m2u2/2(M+m)
The correct Answer is:D
To solve the problem step by step, we will use the principle of conservation of momentum and the formula for kinetic energy.
Step 1: Identify the masses and initial velocities
- Let the mass of the bag be M.
- Let the mass of the bullet be m.
- The initial velocity of the bullet is u (horizontal).
- The initial velocity of the bag is 0 (since it is hanging and at rest).
Step 2: Apply conservation of momentum
According to the conservation of momentum, the total momentum before the collision must equal the total momentum after the collision.
The total initial momentum (before the collision) is:
Initial Momentum=Momentum of bullet+Momentum of bag=m⋅u+M⋅0=m⋅u
Let V be the velocity of the combined system (bag + bullet) just after the collision. The total mass after the collision is M+m.
The total momentum after the collision is:
Final Momentum=(M+m)⋅V
Setting the initial momentum equal to the final momentum gives us:
m⋅u=(M+m)⋅V
Step 3: Solve for the velocity V
Rearranging the equation to solve for V:
V=m⋅uM+m
Step 4: Calculate the kinetic energy of the system after the collision
The kinetic energy KE of the combined system after the collision can be calculated using the formula:
KE=12⋅Total Mass⋅V2
Substituting the total mass and the expression for V:
KE=12⋅(M+m)⋅(m⋅uM+m)2
Step 5: Simplify the kinetic energy expression
Now, simplifying the expression:
KE=12⋅(M+m)⋅m2⋅u2(M+m)2
KE=12⋅m2⋅u2M+m
Conclusion
Thus, the kinetic energy of the system just after the collision is:
KE=m2⋅u22(M+m)
- Let the mass of the bag be M.
- Let the mass of the bullet be m.
- The initial velocity of the bullet is u (horizontal).
- The initial velocity of the bag is 0 (since it is hanging and at rest).
According to the conservation of momentum, the total momentum before the collision must equal the total momentum after the collision.
Initial Momentum=Momentum of bullet+Momentum of bag=m⋅u+M⋅0=m⋅u
Final Momentum=(M+m)⋅V
m⋅u=(M+m)⋅V
Rearranging the equation to solve for V:
V=m⋅uM+m
The kinetic energy KE of the combined system after the collision can be calculated using the formula:
KE=12⋅Total Mass⋅V2
Substituting the total mass and the expression for V:
KE=12⋅(M+m)⋅(m⋅uM+m)2
Now, simplifying the expression:
KE=12⋅(M+m)⋅m2⋅u2(M+m)2
KE=12⋅m2⋅u2M+m
Thus, the kinetic energy of the system just after the collision is:
KE=m2⋅u22(M+m)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct25videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective23videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
A wooden log of mass M and length L is hinged by a frictionless nail at O.A bullet of mass m strikes with velocity v and sticks to it. Find angular velocity of the system immediately after the collision aboutO.
 View Solution
View SolutionA ball of mass 0.2 kg rests on a vertical post of height 5 m. A bullet of mass 0.01 kg, travelling with a velocity Vm/s in a horizontal direction, hits the centre of the ball. After the collision, the ball and bullet travel independently. The ball hits the ground at a distance of 20 m and the bullet at a distance of 100 m from the foot of the post. The velocity V of the bullet is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A bag P (mass M) hangs by a long thread and bullet (mass m) comes horizontally with velocity v and gets caught in the bag. Then for the combined (bag + bullet) system
Amomentum is mvMM+mBkinetic energy is mv22Cmomentum is mv(M+m)MDKinetic energy is m2v22(M+m)
A body of mass a moving with a velocity b strikes a body of mass c and gets embedded into it. The velocity of the systems after collision is
View SolutionThe de Broglie wave length of a riffle bullet of mass 2 grams moving with a velocity of 2m/sec of
View SolutionA circular wooden hoop of mass m and radius R rests fiat on a frictionless surface. A bullet, also of mass m and moving with a velocity v, strikes the hoop and gets embedded in it. The thickness of the hoop is much smaller than R. Find the angular velocity with which the system rotates in after the bullet strikes the hoop.
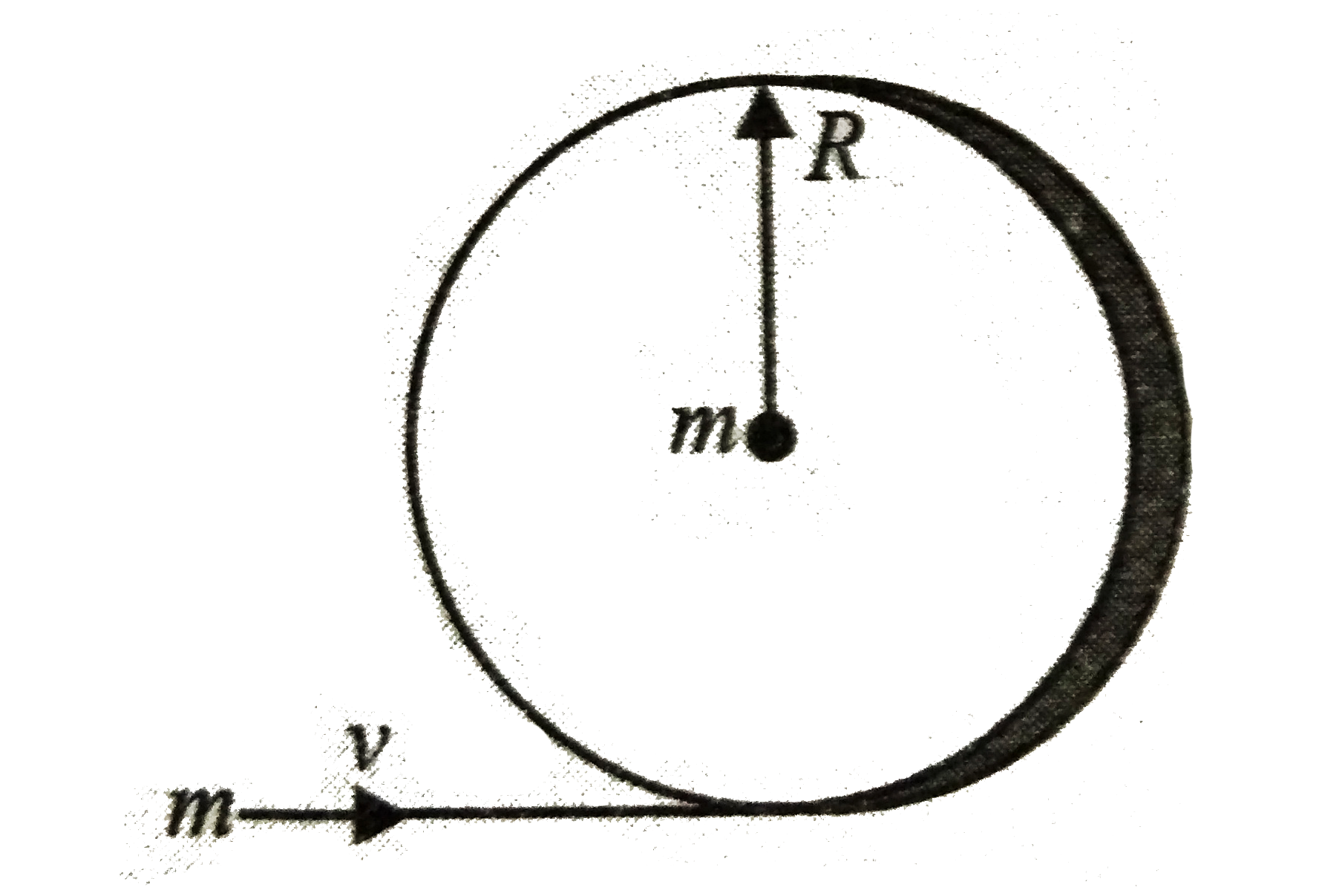 View Solution
View SolutionIf a bullet of mass 5gm moving with velocity 100m/sec, penertates the wooden block upto 6cm. Then the average force imposed by the bullet on the block is
View SolutionA gun of mass M fires a bullet of mass m with a Kinetic energy E. The velocity of recoil of the gun is
View SolutionTwo blocks of masses m and 3m are connected by an inextensible string and the string passes over a fixed pulley which is massless and frictionless. A bullet of mass m moving with a velocity 'u' hits the hanging block of mass 'm' and gets exbedded in it. Find the height through which block A rises after the collision.
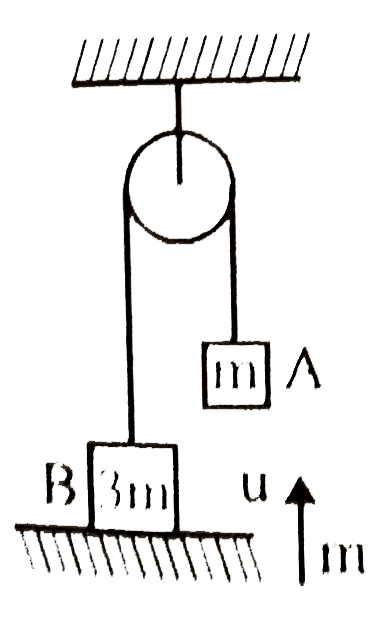 View Solution
View SolutionA block A of mass 2m is hanging from a vertical massless spring of spring constant k and is in equilibrium. Another block B of mass m strikes the block A with velocity u and sticks to it as shown in the figure. The magnitude of the acceleration of the combined system of the blocks just after the collision is
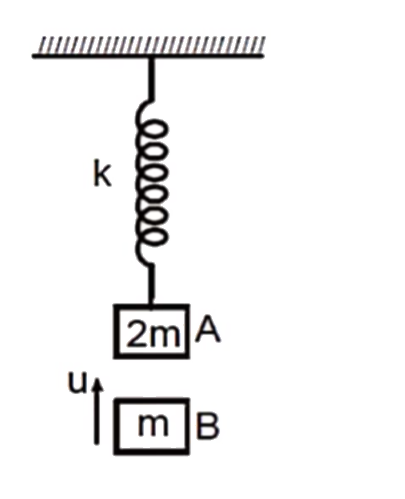 View Solution
View Solution

