Question

Two particles of equal mass in are projected from the ground with speeds $v_1$ and $v_2$ at angles ${\theta }_1$, and ${\theta }_2$ as shown in the figure. Given ${\theta }_2>{\theta }_1$ and $v_1{\cos \theta }_1=v_2{\cos \theta }_2$Which statement/s is/are correct?

Options

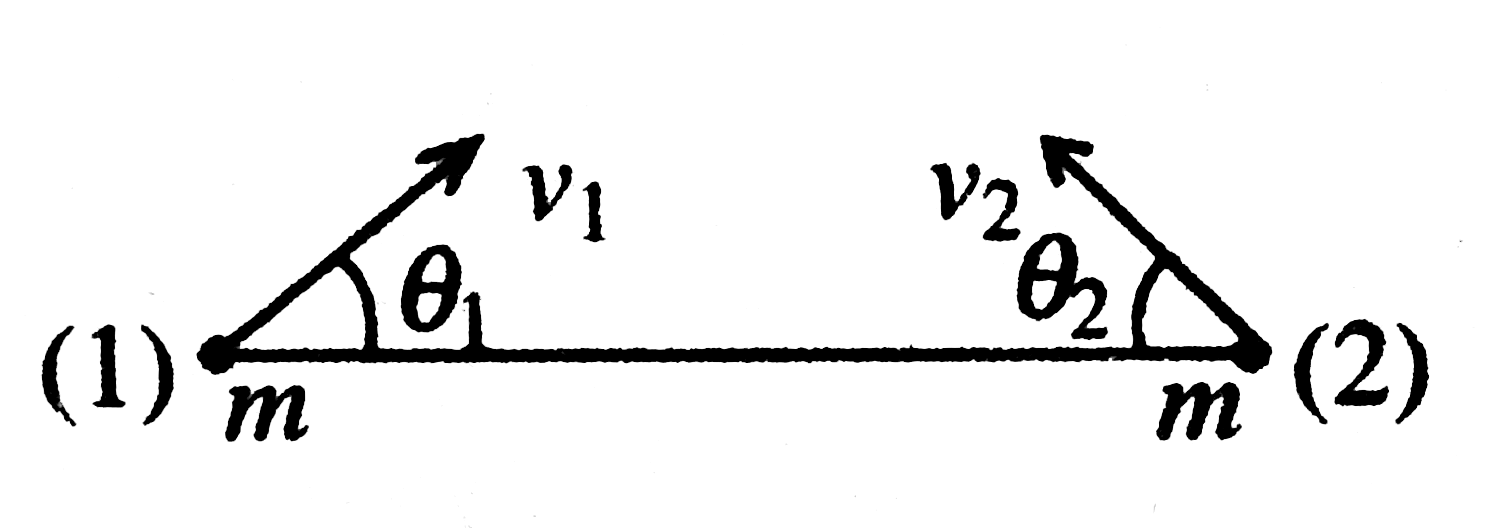
A. Centre of mass of particles will move along a vertical line.
B. Centre of mass of particles will move along a line inclined at some angle with vertical.
C. Particle `'1'` will be above vertical. centre of mass level when both particles are in air.
D. Particle `'2'` will be above centre of mass level both particles are in air.

Answer

A::D

Explanation

`v_(cm-x)=(mv_(1)costheta_(1)m(-v_(2)costheta_(2)))/(m+m)=0`
So horizontal velocity of centre of mass is zero. Hence centre of masss will move in vertical direction.
Now `v_(2)costheta_(2)=v_(1)costheta_(1)`
`implies v_(2)/v_(1)=(costheta_(1))/(costheta_(2))gt1` (`:'theta_(2)gttheta_(1))`
`implies v_(2)gtv_(1)`
`implies v_(2)sintheta_(2)gt gt v_(1)sintheta_(1)v_(2)sintheta_(2)`
At any time particle 2 will be greater height than particle 1. so particle 2 will be above centre of man level.