Three spheres, each of mass m, can slide freely on a frictionless, horizontal surface. Spheres A and B are attached to an inextensible, inelastic cord of length l and are at rest in the position shown where sphere B is struck by sphere C which is moving to the right with a velocity v0. Knowing that the cord is taut where sphere B is struck by sphere C and assuming 'head on' inelastic impact between B and C, we cannot conserve kinetic energy of the entire system.
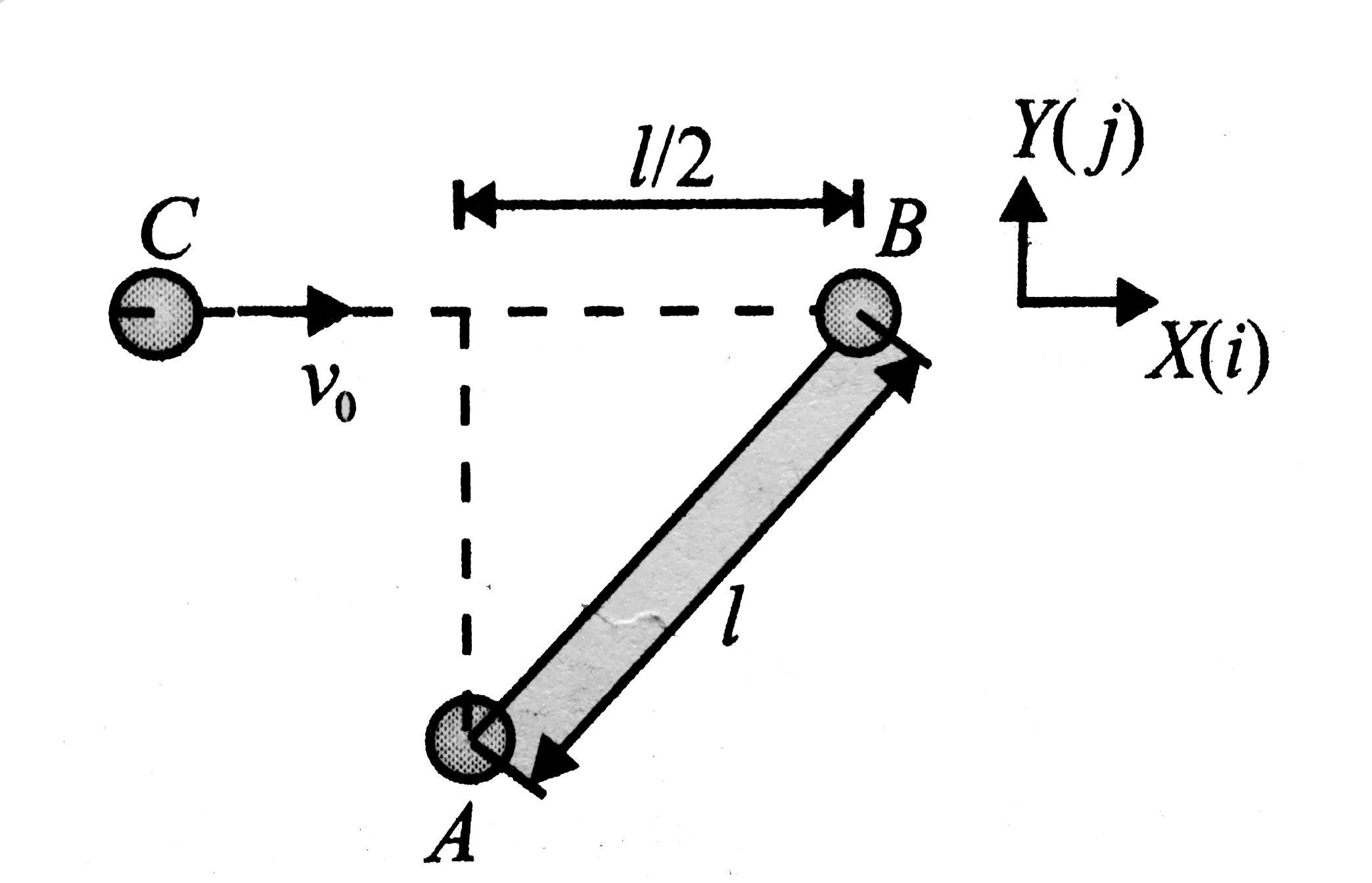
The magnitude of velocity of A immediately after collision is
ˆj
12ˆi+√32ˆj
ˆj
none of these
The correct Answer is:B
velocity of A:→v1=v1cosθˆi+v1sinθˆj
⇒→v1=cosθˆi+sinθˆj=12ˆi+√32ˆj
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Integer16videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
Three spheres, each of mass m, can slide freely on a frictionless, horizontal surface. Spheres A and B are attached to an inextensible, inelastic cord of length l and are at rest in the position shown where sphere B is struck by sphere C which is moving to the right with a velocity v0. Knowing that the cord is taut where sphere B is struck by sphere C and assuming 'head on' inelastic impact between B and C, we cannot conserve kinetic energy of the entire system.
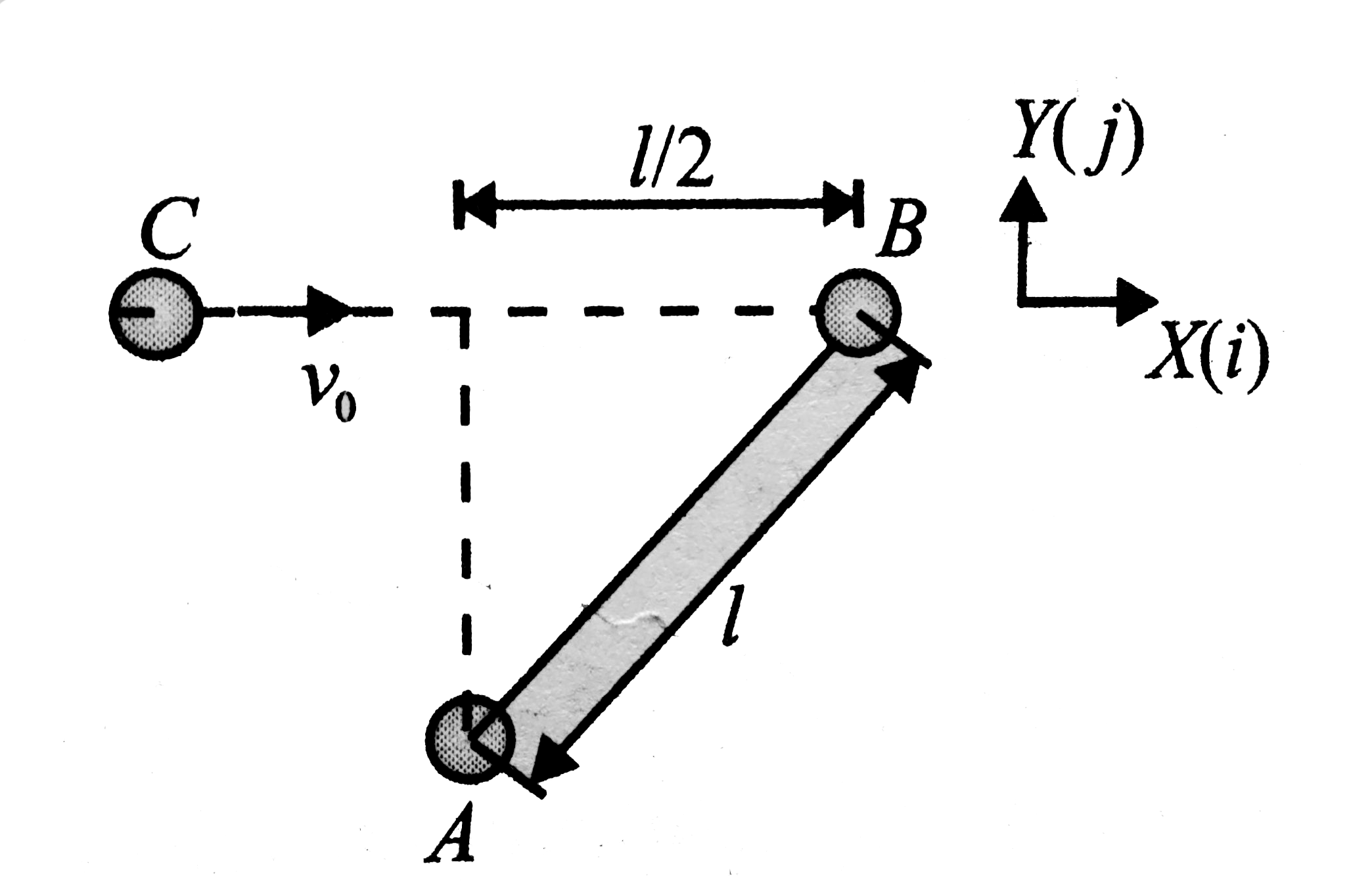
If velocity of C immediately after collision becomes v02 in the initial direction of motion, the impulse due to string on sphere A isView SolutionThree spheres, each of mass m, can slide freely on a frictionless, horizontal surface. Spheres A and B are attached to an inextensible, inelastic cord of length l and are at rest in the position shown where sphere B is struck by sphere C which is moving to the right with a velocity v0. Knowing that the cord is taut where sphere B is struck by sphere C and assuming 'head on' inelastic impact between B and C, we cannot conserve kinetic energy of the entire system.
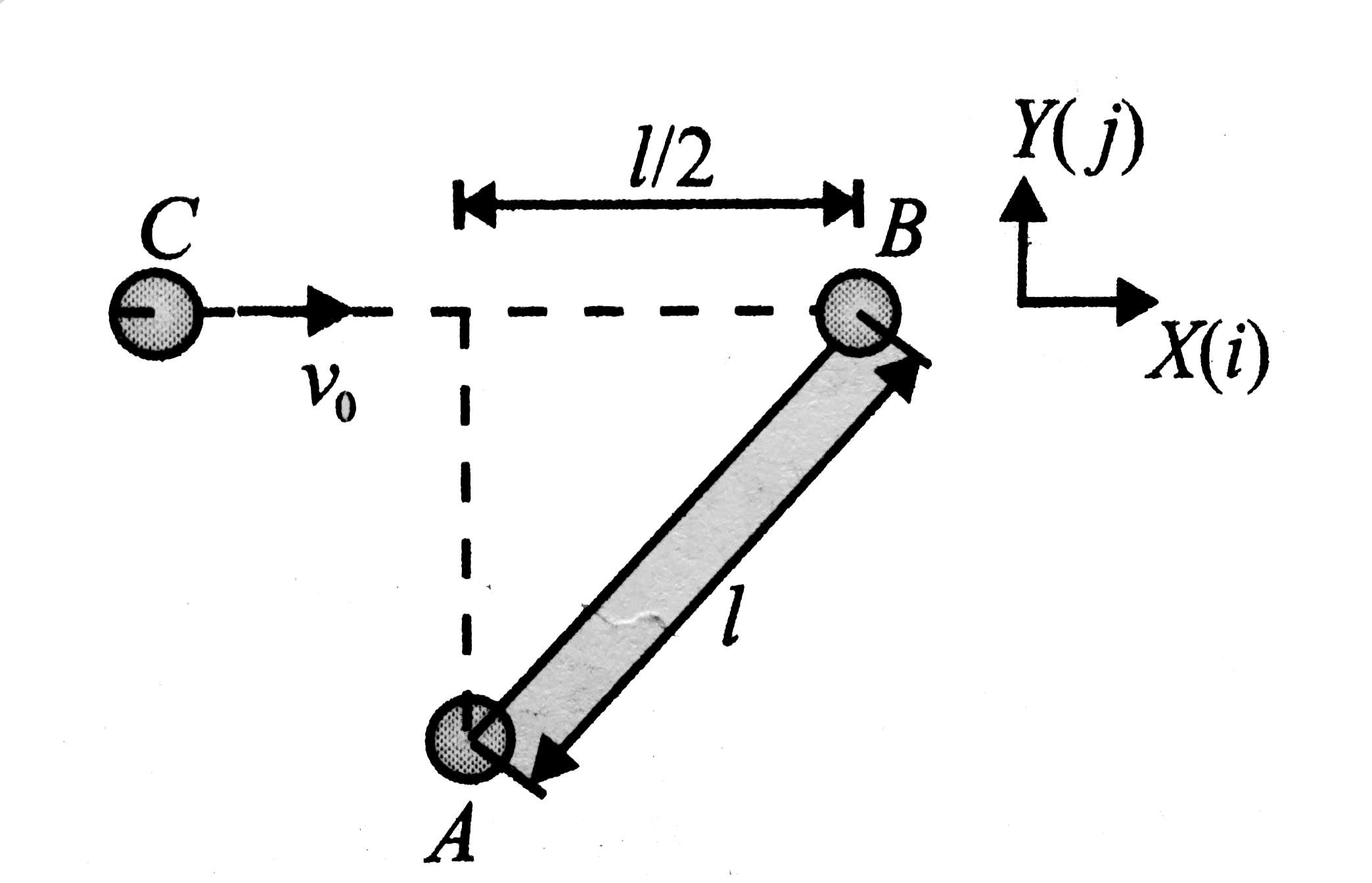 The velocity of B immediately after collision is along unit vectorView Solution
The velocity of B immediately after collision is along unit vectorView SolutionThree spheres, each of mass m, can slide freely on a frictionless, horizontal surface. Spheres A and B are attached to an inextensible, inelastic cord of length l and are at rest in the position shown where sphere B is struck by sphere C which is moving to the right with a velocity v0. Knowing that the cord is taut where sphere B is struck by sphere C and assuming "Head on" inelastic impact between B and C, we can 't conserve kinetic energy of entire system.
If velocity of C immediately after collision becomes v02 in the initial direction of motion, the impulse due to string on sphere A is
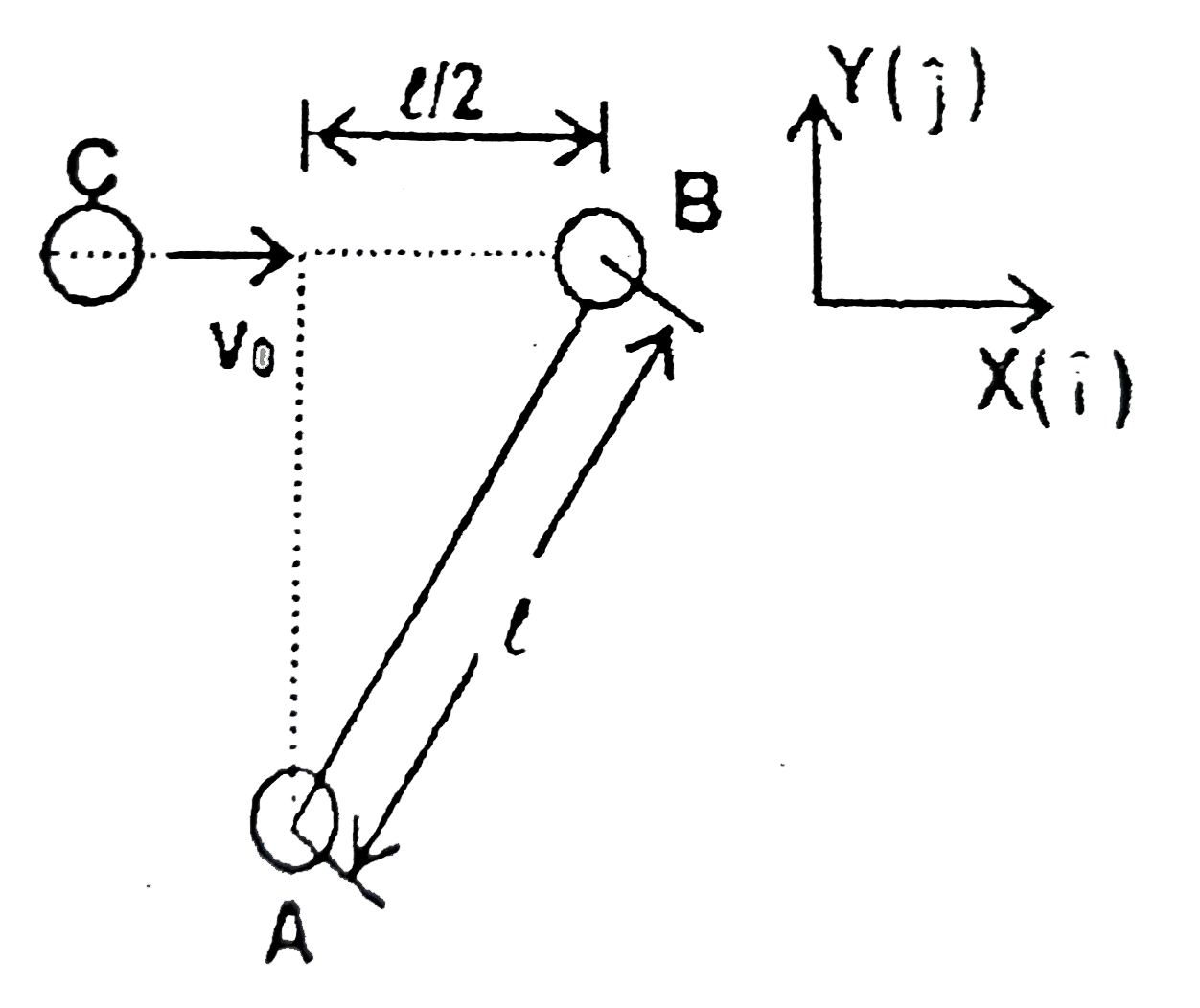 View Solution
View SolutionThree solid spheres each of mass m and radius R are released from the position shown in Fig. What is the speed of any one sphere at the time of collision?
 View Solution
View SolutionA chain of length l and mass m lies on the surface of a smooth sphere of radius R>l with one end tied to the top of the sphere.
View SolutionA sphere rolls on a horizontal surface. Is there any point of the sphere which has a vertical velocity?
View SolutionA sphere of mass m slides with velocity v on as frictionless surface towards a smooth inclined wall as shown in figure. If the collision with the wall is perfectly elastic find a. the impulse imparted by the wall on the sphere b the impulse imparted by the floor on the sphere.
 View Solution
View SolutionInitially the spheres A and B are at potentials VA and VB. Find the potential of A when sphere B is earthed.
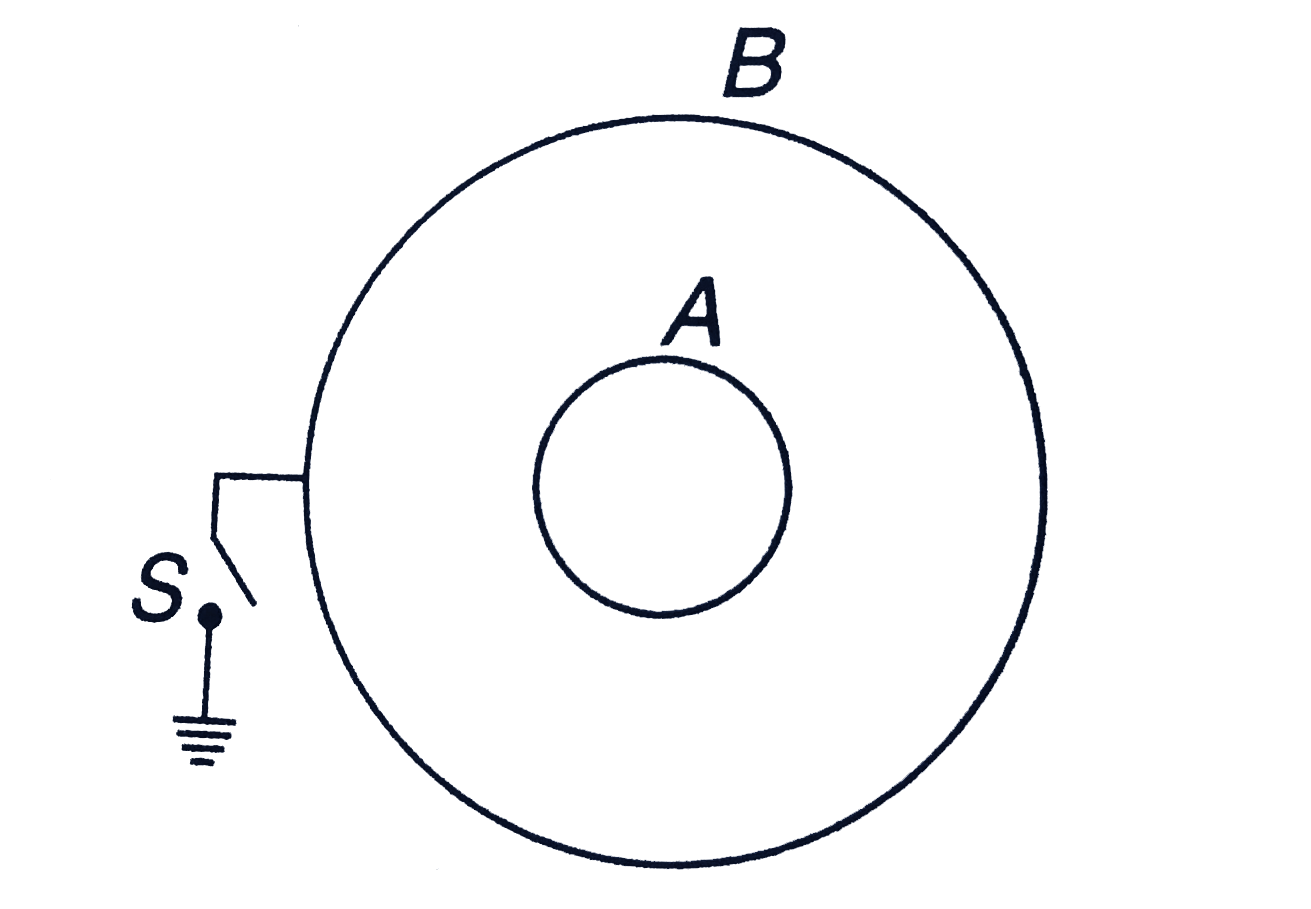 View Solution
View SolutionInitially the spheres A and B are at potentials VA and VB. Find the potential of A when sphere B is earthed.
 View Solution
View SolutionThree identical spheres each of radius .R. are placed on a horizontal surface touching one another. If one of the spheres is removed, the shift in the centre of mass of the system is
View Solution

