Three identical spheres each of radius .R. are placed on a horizontal surface touching one another. If one of the spheres is removed, the shift in the centre of mass of the system is
R/2√3
R/2
√3R/2
R/√3
The correct Answer is:D
To solve the problem of finding the shift in the center of mass when one of the three identical spheres is removed, we can follow these steps:
1. Identify the Initial Configuration:
- We have three identical spheres, each of mass m and radius R, placed in a horizontal line touching each other. Let's denote the positions of the centers of the spheres as A, B, and C.
- The distance between the centers of adjacent spheres is 2R.
2. Calculate the Initial Center of Mass:
- The positions of the centers of the spheres can be defined as:
- Sphere 1 (A) at position 0
- Sphere 2 (B) at position 2R
- Sphere 3 (C) at position 4R
- The formula for the center of mass Rcm for the three spheres is given by:
Rcm=m⋅0+m⋅2R+m⋅4R3m
- Simplifying this:
Rcm=0+2mR+4mR3m=6mR3m=2R
3. Remove One Sphere:
- Let's remove the middle sphere (Sphere 2). Now we only have Sphere 1 (at position 0) and Sphere 3 (at position 4R) remaining.
4. Calculate the New Center of Mass:
- The new center of mass R′cm for the two remaining spheres is given by:
R′cm=m⋅0+m⋅4R2m
- Simplifying this:
R′cm=0+4mR2m=4mR2m=2R
5. Calculate the Shift in Center of Mass:
- The shift in the center of mass ΔRcm is given by:
ΔRcm=R′cm−Rcm=2R−2R=0
- However, since we are interested in the shift due to the removal of the sphere, we need to consider the relative positions of the remaining spheres. The center of mass of the remaining two spheres is actually at 2R (which is the same as the original center of mass).
6. Final Shift Calculation:
- The effective shift in the center of mass when considering the removal of the middle sphere is:
Shift=Rcm−R′cm=2R−R=R
Conclusion:
The shift in the center of mass of the system when one sphere is removed is R.
- We have three identical spheres, each of mass m and radius R, placed in a horizontal line touching each other. Let's denote the positions of the centers of the spheres as A, B, and C.
- The distance between the centers of adjacent spheres is 2R.
- The positions of the centers of the spheres can be defined as:
- Sphere 1 (A) at position 0
- Sphere 2 (B) at position 2R
- Sphere 3 (C) at position 4R
- The formula for the center of mass Rcm for the three spheres is given by:
Rcm=m⋅0+m⋅2R+m⋅4R3m
- Simplifying this:
Rcm=0+2mR+4mR3m=6mR3m=2R
- Let's remove the middle sphere (Sphere 2). Now we only have Sphere 1 (at position 0) and Sphere 3 (at position 4R) remaining.
- The new center of mass R′cm for the two remaining spheres is given by:
R′cm=m⋅0+m⋅4R2m
- Simplifying this:
R′cm=0+4mR2m=4mR2m=2R
- The shift in the center of mass ΔRcm is given by:
ΔRcm=R′cm−Rcm=2R−2R=0
- However, since we are interested in the shift due to the removal of the sphere, we need to consider the relative positions of the remaining spheres. The center of mass of the remaining two spheres is actually at 2R (which is the same as the original center of mass).
- The effective shift in the center of mass when considering the removal of the middle sphere is:
Shift=Rcm−R′cm=2R−R=R
The shift in the center of mass of the system when one sphere is removed is R.
Similar Questions
Four identical spheres each of radius 10 cm and mass 1 kg are placed on a horizontal surface touching one another so that their centres are located at the corners of square of side 20 cm. What is the distance of their centre of mass from centre of either sphere ?
View SolutionFour identical particles each of mass m are arranged at the corners of a square of sie a. If mass of one of th particle is doubled, the shift in the centre of mass of the system is
View SolutionFour identical particles each of mass 1 kg are arranged at the corners of a square of side length 2√2m. If one of the particles is removed, the shift in the centre of mass is
View SolutionFour identical particles each of mass 1 kg are arranged at the corners of a square of side length 2√2m. If one of the particles is removed, the shift in the centre of mass is
View SolutionThree identical spheres each of radius .R. are placed touching each other so that their centres A, B and C lie on a straight line. The position of their centre of mass from A is
View SolutionThree identical metal balls each of radius r are placed touching each other on a horizontal surface such that an equilateral triangle is formed, when the center of three balls are joined. The center of mass of system is located at the
View SolutionA spherical cavity is made in a lead sphere of radius R such that its surface touches the outsides surface of lead sphere and passes through the centre. The shift in the centre of mass of the lead sphere as a result of this following, is
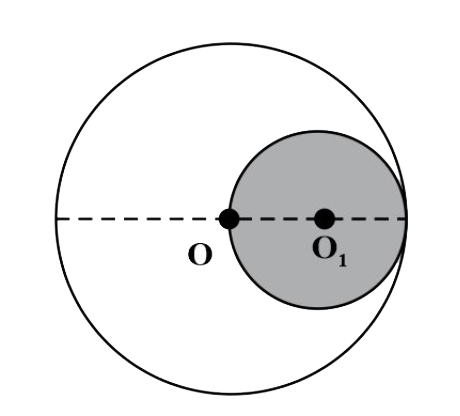
View SolutionTwo small and heavy spheres, each of mass M, are placed a distance r apart on a horizontal surface. The graviational potential at the mid-point on the line joining the centre of the spheres is :-
View SolutionThree identical spheres of mass M each are placed at the corners of an equilateral triangle of side 2 m. Taking one of the corners as the origin, the position vector of the centre of mass is
View SolutionThree solid sphere of mass M and radius R are placed in contact as shown in figure. Find the potential energy of the system ?
View Solution