Find the instantneous axis of rotation of a rod length l when its end A moves with a velocity →vA=Vi and the rod rotates with an angular velocity →ω=−v2lˆk.
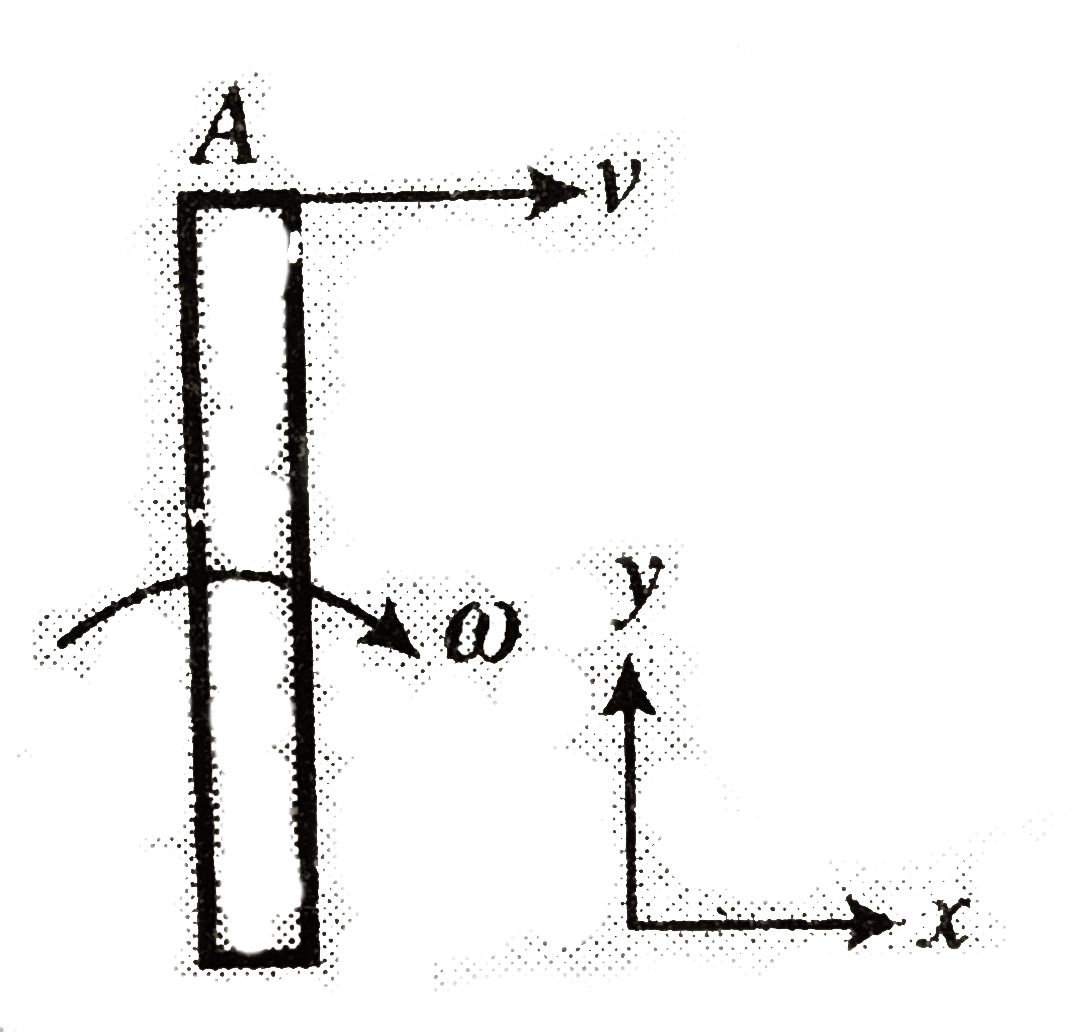
Let us choose the point P as ICR in the extended rod. We can say ICR is a point of zero velocity. So we can write
→vP=→vP,A+→vA
we have →vP=0
Hence →vP,A=→vA=0
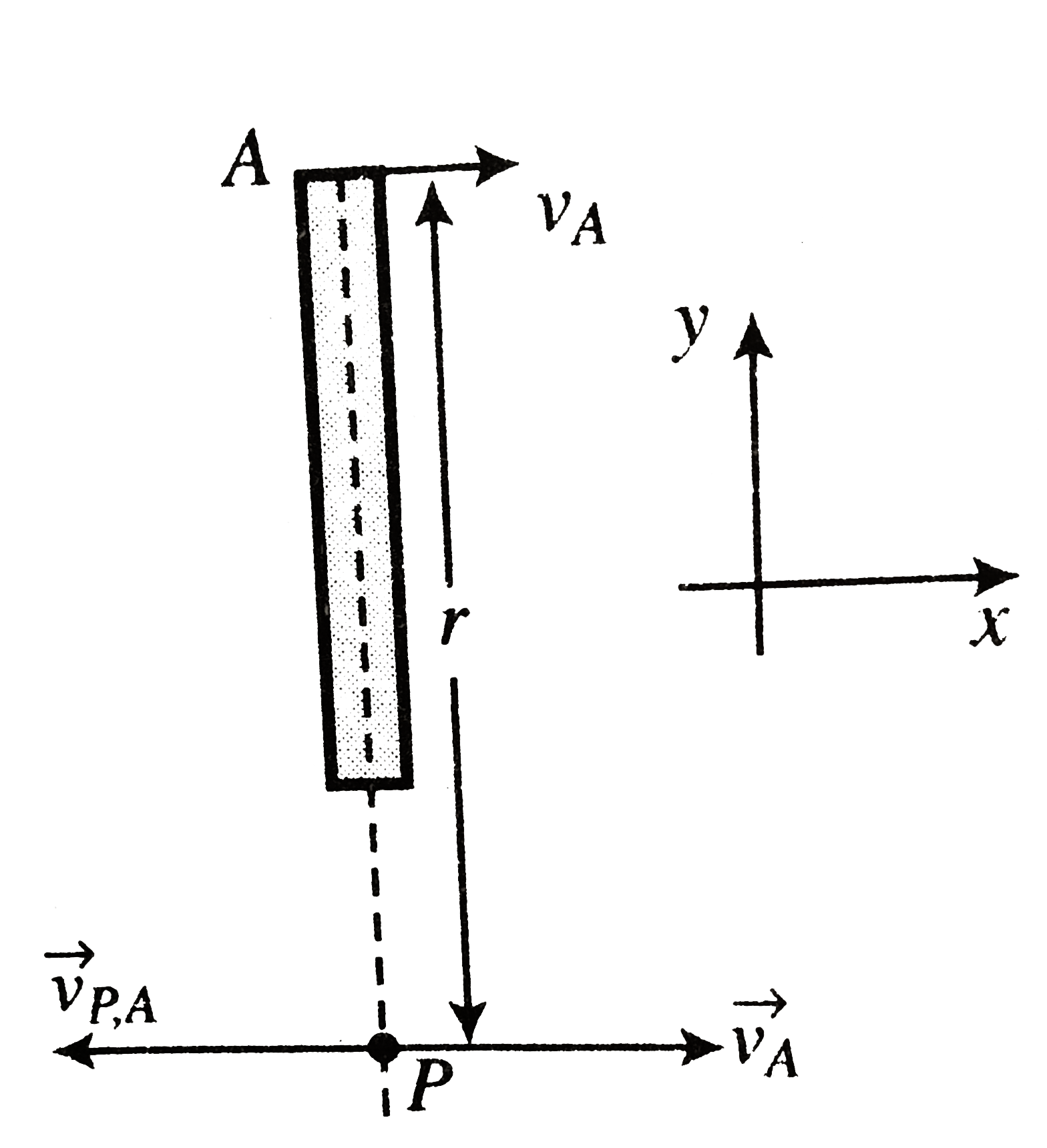
Here →–––(A)=vˆi and →vP,A=−ωˆi
Hence −ωrˆi+vˆi=0
⇒v=ωr
or r=vω=v(v2l)=2l
Hence ICR will be located at a distance 2l from A.
Method 2
The instantaneous centre of rotation will be lie on the perpendicular line at point A with →vA.
The ICR will lie at distance AP+|→vA|ω=vv2l=2l
or at a distance 2l from point A.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Solved Examples9videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.16videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
Knowledge Check
- Question 1 - Select One
The linear velocity of rotating body is given by →v=→ω×→r where →ω is the angular velocity and →r is the radius vector. The angular velocity of body →ω=ˆi−2ˆj+2ˆk and this radius vector →r=4ˆj−3ˆk, then |→v| is
A√29 unitsB√31 unitsC√37 unitsD√41 units
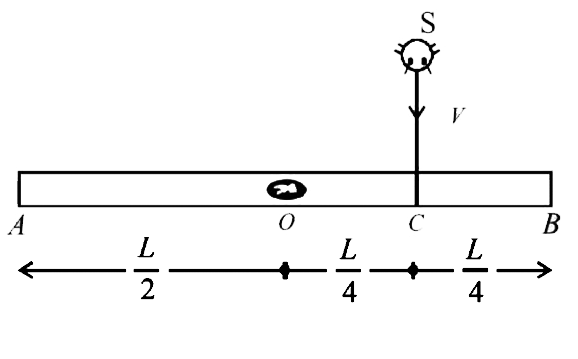
A homogeneous rod AB of length L = 1.8 m and mass M is pivoted at the center O in such a way that it can rotate it can rotate freely position. An insect S of the same mass M falls vertically with speed V on the point C, midway between the points O and B. Immediately after falling, the insect moves towards the end B such that the rod rotates with a constant angular velocity omega.
(a) Determine the angular velocity ω in terms of V and L.
(b) If the insect reaches the end B when the rod has turned through an angle of 90∘, determine V.
 View Solution
View SolutionA conducting rod of length 1 is moving on a horizontal smooth surface. Magnetic field in the region is vertically downward and magnitude B0. If centre of mass (COM) of the rod is translating with velocity v0 and rod rotates about COM with angular velocity v0/l, then potential difference between points O and A will be
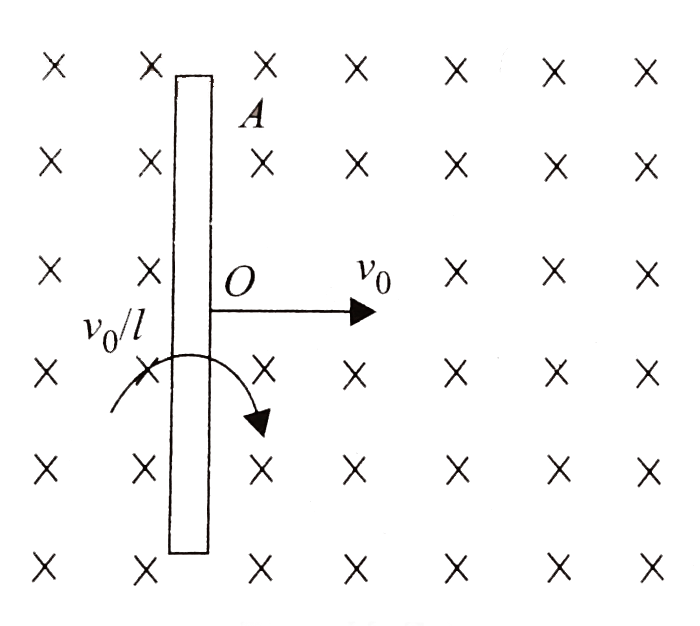 View Solution
View SolutionA rod of length l is pivoted smoothly at O is resting on a block of height h. If the block moves with a constant velocity V, pick the correct alternatives about angular velocity of rod :
 View Solution
View SolutionA rod AB of length 2m moves in horizontal x−y plane. At any instant end a of the rod is at origin and has velocity →vA=2ˆi+vyˆj. The other end B at the same instant is moving with velocity →vB=3ˆi+6ˆj. The rod makes an angle of 30∘ with the x−axis at this instant (see figure)
The magnitude of angular velocity of the rod is
 View Solution
View SolutionA rod of length l is moving in a vertical plane (x−y) when the lowest point A of the rod is moved with a velocity v. find the a angular velocity of the rod and b velocity of the end B.
 View Solution
View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:View Solution


