A small block B of mass m2 is placed on another block A of mass m1 A constant horizontal force F is applied to the block A. All the surfaces are assumed to be frictionless. Find the acceleration of center of mass of the system
m22Fm1+m2
Fm1+m2
Fm1
m21Fm1+m2
To find the acceleration of the center of mass of the system consisting of two blocks A and B, we can follow these steps:
Step 1: Understand the System
We have two blocks:
- Block A with mass m1
- Block B with mass m2
A constant horizontal force F is applied to block A. The surfaces are frictionless.
Step 2: Identify the Forces
Since the surfaces are frictionless, the only horizontal force acting on block A is the applied force F. Block B does not experience any horizontal forces because it is resting on block A without friction.
Step 3: Write the Equation of Motion for Block A
Using Newton's second law, the acceleration a1 of block A can be expressed as:
F=m1⋅a1
From this, we can solve for a1:
a1=Fm1
Step 4: Determine the Acceleration of Block B
Since block B is resting on block A and there is no friction, it does not accelerate horizontally. Thus, the acceleration a2 of block B is:
a2=0
Step 5: Calculate the Acceleration of the Center of Mass
The acceleration of the center of mass acm of the system can be calculated using the formula:
acm=m1⋅a1+m2⋅a2m1+m2
Substituting the values we have:
acm=m1⋅(Fm1)+m2⋅0m1+m2
This simplifies to:
acm=Fm1+m2
Final Answer
Thus, the acceleration of the center of mass of the system is:
acm=Fm1+m2
We have two blocks:
- Block A with mass m1
- Block B with mass m2
Since the surfaces are frictionless, the only horizontal force acting on block A is the applied force F. Block B does not experience any horizontal forces because it is resting on block A without friction.
Using Newton's second law, the acceleration a1 of block A can be expressed as:
F=m1⋅a1
From this, we can solve for a1:
a1=Fm1
Since block B is resting on block A and there is no friction, it does not accelerate horizontally. Thus, the acceleration a2 of block B is:
a2=0
The acceleration of the center of mass acm of the system can be calculated using the formula:
acm=m1⋅a1+m2⋅a2m1+m2
Substituting the values we have:
acm=m1⋅(Fm1)+m2⋅0m1+m2
This simplifies to:
acm=Fm1+m2
Thus, the acceleration of the center of mass of the system is:
acm=Fm1+m2
Similar Questions
A small block B is placed on another block A of mass 5 kg and length 20 cm. Initially, the block B is near the right end of block A. A constant horizontal force of 10 N is applied to the block A. All the surfaces are assumed frictionless. Find the time elapsed before the block B separates from A.
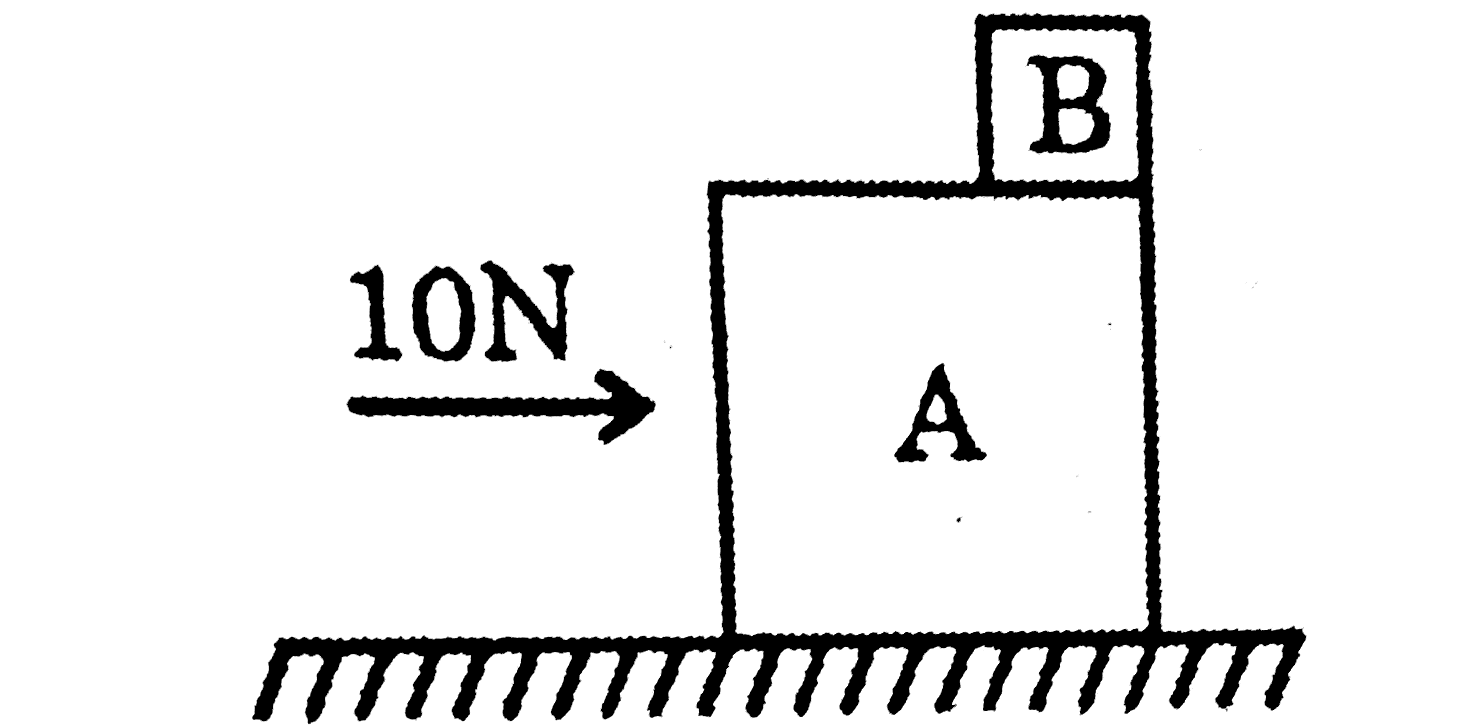
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m as shown in A horizontal force F is applied to one end of the rope. Find
(a) the acceleration of the rope and block
(b) the force that the rope exerts on the block
(c) the tension in the rope at its mid point

View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA block of unknown mass is at rest on a rough, horizontal surface. A horizontal force F is applied to the block. The graph in the figure shows the acceleration of the block with respect to the applied force. The mass of the block is

View SolutionThree block A,B,and C of mass m1,m2 and m3, respectively are resting one on top of the other as shown in fig. A horizontal force F is applied on block B. Assuming all the surfaces are frictionless, calculate (1) acceleration of block A, block B, and block C, (2) normal reactions between A and B, B and C, and between C and ground .

View Solution
A block B is placed over a cart which in turn lies over a smooth horizontal floor. Block A and Block C are connected to block B with light inextensible strings passing over light frictionless pulleys fixed to the cart as shown. Initially the blocks and the cart are at rest. All the three blocks have mass m and the cart has mass M(M=3m). Now a constant horizontal force of magnitude F is applied to block A towards right.
Assuming friction to be absent everywhere, the magnitude of acceleration of cart at the shoen instant is
View SolutionA block of mass m is placed on the block of mass M as shown in figure. The horizontal force →F acts on M during time interval t. If the horizontal surface is smooth, assuming no relative sliding between the blocks, find the
a. work done by friction on the blocks
b. work done by →F on the lower block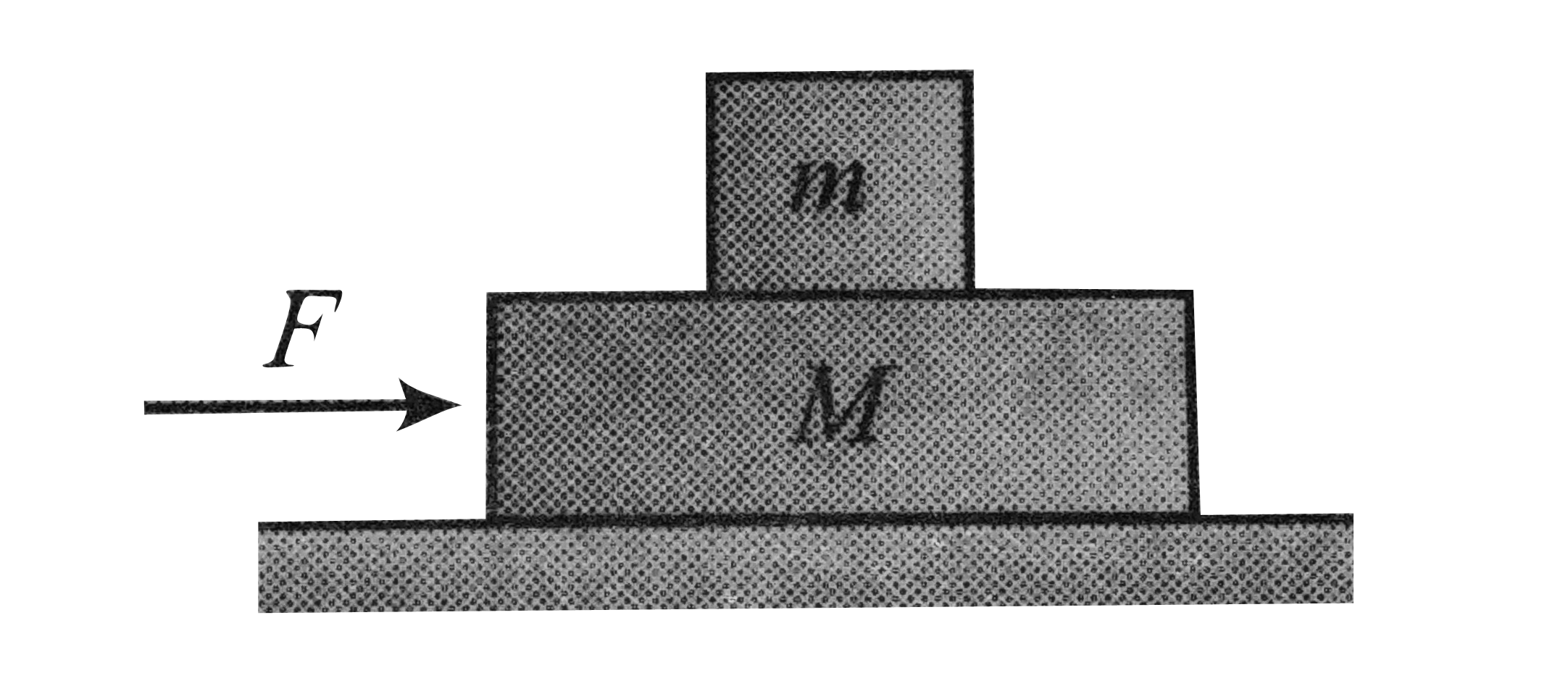
View SolutionA block of mass m is placed on another block of mass M lying on a smooth horizontal surface as shown in the figure. The co-efficient of friction between the blocks is μ. Find the maximum horizontal force F (in Newton) that can be applied to the block M so that the blocks together with same acceleration? (M=3kg,m=2kg,μ=0.1,g=10m/s2)

View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.

What is acceleration of centre of mass of system at the instant of maximum elongation of spring
View SolutionA block of mass m is kept over another block of mass M nd the system rests on a horizontal force F acting on the lower block produces an accelertion F2(m+M) in the system the two blocks always move together. A. Find the coefficient of kinetic frictioin between the bigger block and th horizontal surface. b. find the frictional force acting on the smaller block. c. Find the work done by the force of friction on the smaller block by the bigger block during a displacement d of the system.
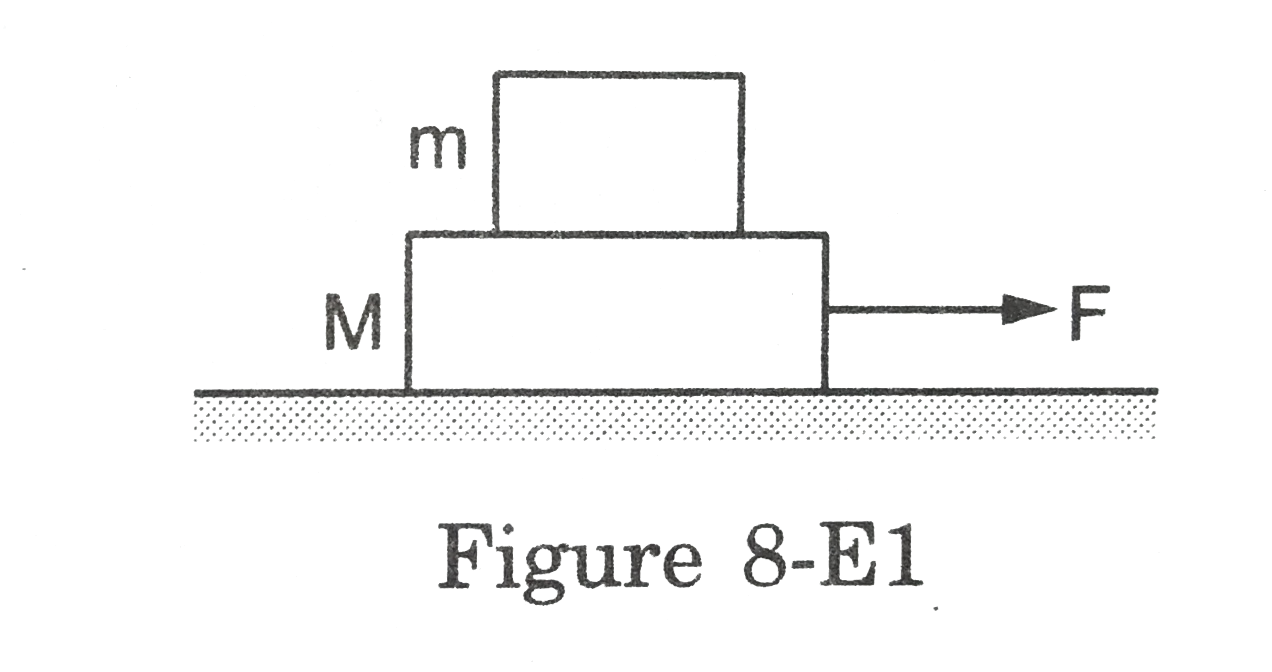
View Solution
