A rigid body is rotating about a vertical axis. In t second, the axis gradually becomes horizontal. But the rigid body continues to make v rotations per second throughout the time interval of 1 second. If the moment of inertia I of the body about the axis of rotation can he taken as constant, then the torque acting on the body is
2πvI
2√2πvI
2√2πvtI
2√2πvltI
The correct Answer is:D
→τ=I→α or →τI=I(→ω2−→ω1)t
But |ω2−→ω1|=√ω22+ω21=√2ω=√2×2πv
τ=It×2√2πv or τ=2√2πvIt
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct9videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension28videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective13videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
The moment of inertia of a body about a given axis of rotation depends upon :-
View SolutionA : For a body to be in rotational equilibrium the net torque acting on the body about any point is zero.
R : For net torque to be zero, net force should also be zero.View SolutionA wheel rotating at an angular speed of 20 rad/s is brought to rest by a constant torque in 4.0 seconds. If the moment of inertia of the wheel about the axis of rotation is 0.20 kg−m2 find the work done by the torque in the first two seconds.
View SolutionA body is rotating with angular momentum L. If I is its moment of inertia about the axis of rotation is I, its kinetic energy of rotation is
View SolutionIn the figure shown ABCD is a lamina of mass 12kg. The moment of inertia of the given body about an axis passing through D, and perpendicular to the plane of the body is
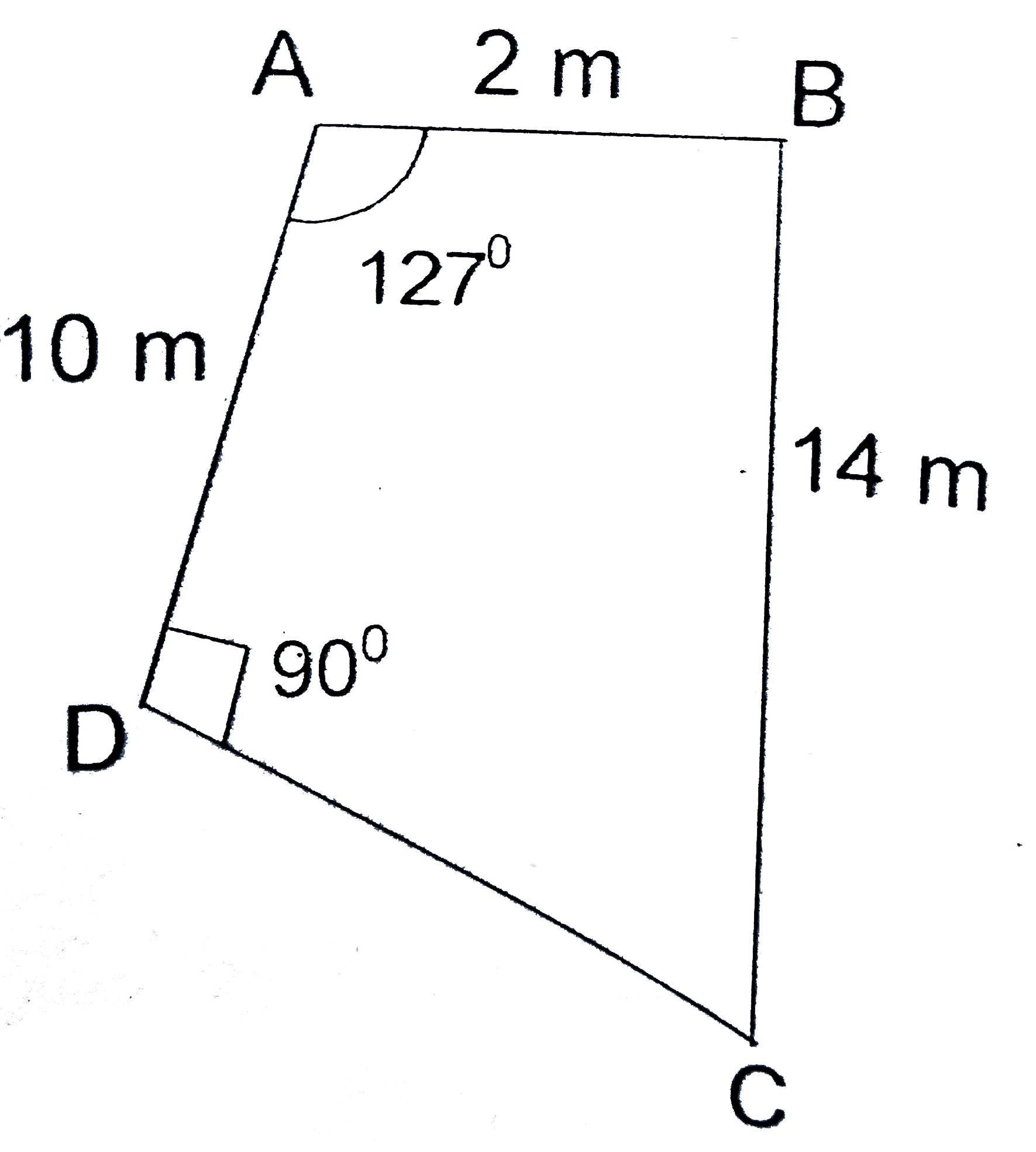 View Solution
View SolutionA body is rotating uniformly about a vertical axis fixed in an inertial frame. The resultant force on a particle of the body not on axis is
View SolutionA uniform rod of mass m and length l0 is rotating with a constant angular speed ω about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle θ to the vertical (axis of rotation).
View SolutionA flywheel is making 3000π revolutions per minute about its axis. If the moment of inertia of the flywheel about that axis is 400 kgm2, its rotational kinetic energy is :
View SolutionIf a body of moment of inertia 2kgm2 revolves about its own axis making 2 rotations per second, then its angular momentum (in J s) is
View SolutionWhen the axis of rotation of a body changes does moment of inertia also change ? Why ?
View Solution

