A uniform plane sheet of metal in the form of a triangle ABC has BC>AB>AC. Its moment of inertia will be smallest
about AC as axis
about AB as axis
about BC as axis
with a line through C normal to its plane as axis,
The correct Answer is:C
To determine the moment of inertia of a uniform plane sheet of metal in the form of triangle ABC, where BC > AB > AC, we need to analyze the distribution of mass relative to the axes of rotation.
1. Understanding Moment of Inertia:
The moment of inertia (I) of a body depends on how the mass is distributed with respect to the axis of rotation. It is calculated using the formula:
I=∫r2dm
where r is the distance from the axis of rotation to the mass element dm.
2. Identifying the Triangle:
We have triangle ABC with sides such that BC>AB>AC. This means that side BC is the longest, followed by AB, and AC is the shortest.
3. Choosing the Axis of Rotation:
To find which axis gives the smallest moment of inertia, we need to consider the axes along each side of the triangle. We will analyze the moment of inertia about the sides BC, AB, and AC.
4. Analyzing Mass Distribution:
- About Side BC: The distance of the mass elements from the axis (BC) will be the shortest for the other two sides (AB and AC). This means that the mass is distributed closer to the axis, resulting in a smaller moment of inertia.
- About Side AB: The distance from the axis (AB) to the mass elements (AC and BC) will be greater compared to the axis BC, leading to a larger moment of inertia.
- About Side AC: Similarly, the distance from the axis (AC) to the mass elements (AB and BC) will also be larger than that for axis BC, resulting in a larger moment of inertia.
5. Conclusion:
Since the mass distribution is closest to the axis when rotating about side BC, the moment of inertia will be smallest about this axis. Thus, the moment of inertia of the triangle ABC will be smallest when calculated about side BC.
Final Answer:
The moment of inertia of the uniform plane sheet of metal in the form of triangle ABC will be smallest about side BC.
The moment of inertia (I) of a body depends on how the mass is distributed with respect to the axis of rotation. It is calculated using the formula:
I=∫r2dm
where r is the distance from the axis of rotation to the mass element dm.
We have triangle ABC with sides such that BC>AB>AC. This means that side BC is the longest, followed by AB, and AC is the shortest.
To find which axis gives the smallest moment of inertia, we need to consider the axes along each side of the triangle. We will analyze the moment of inertia about the sides BC, AB, and AC.
- About Side BC: The distance of the mass elements from the axis (BC) will be the shortest for the other two sides (AB and AC). This means that the mass is distributed closer to the axis, resulting in a smaller moment of inertia.
- About Side AB: The distance from the axis (AB) to the mass elements (AC and BC) will be greater compared to the axis BC, leading to a larger moment of inertia.
- About Side AC: Similarly, the distance from the axis (AC) to the mass elements (AB and BC) will also be larger than that for axis BC, resulting in a larger moment of inertia.
Since the mass distribution is closest to the axis when rotating about side BC, the moment of inertia will be smallest about this axis. Thus, the moment of inertia of the triangle ABC will be smallest when calculated about side BC.
The moment of inertia of the uniform plane sheet of metal in the form of triangle ABC will be smallest about side BC.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
AD is a median of triangle ABC. Prove that : AB+AC>2AD
View SolutionAD is a median of triangle ABC. Prove that : AB+BC+AC>2AD
View SolutionA thin uniform metallic triangular sheet of mass M has sides AB=BC=L. What is its moment of inertia about axis AC lying in plane of sheet ?

View SolutionD is a point in side BC of triangle ABC. If AD>AC, show that AB>AC.
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L as shown in the figure. Find the moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC

View SolutionAn equilateral triangle ABC is cut from a thin solid sheet of wood .(see figure ) D,E and F are the mid-points of its sides as shown and G is the centre of the triangle.The moment of inertia of the triangle about an axis passing through G and perpendicular to the plane to the triangle is I0 If the smaller triangle DEF is removed from ABC , the moment of inertia of the remaining figure about the same axis is I. Then :

View SolutionIf D any point on the BC of an isosceles triangle ABC then prove that AB>AD and AC>AD.

View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side l (as shown in the figure).
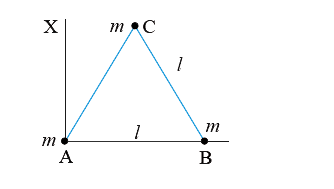
The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, will be:
View SolutionFigure shows a thin metallic triangular sheet ABC. The mass of the sheet is M. The moment of inertia of the sheet about side AC is :
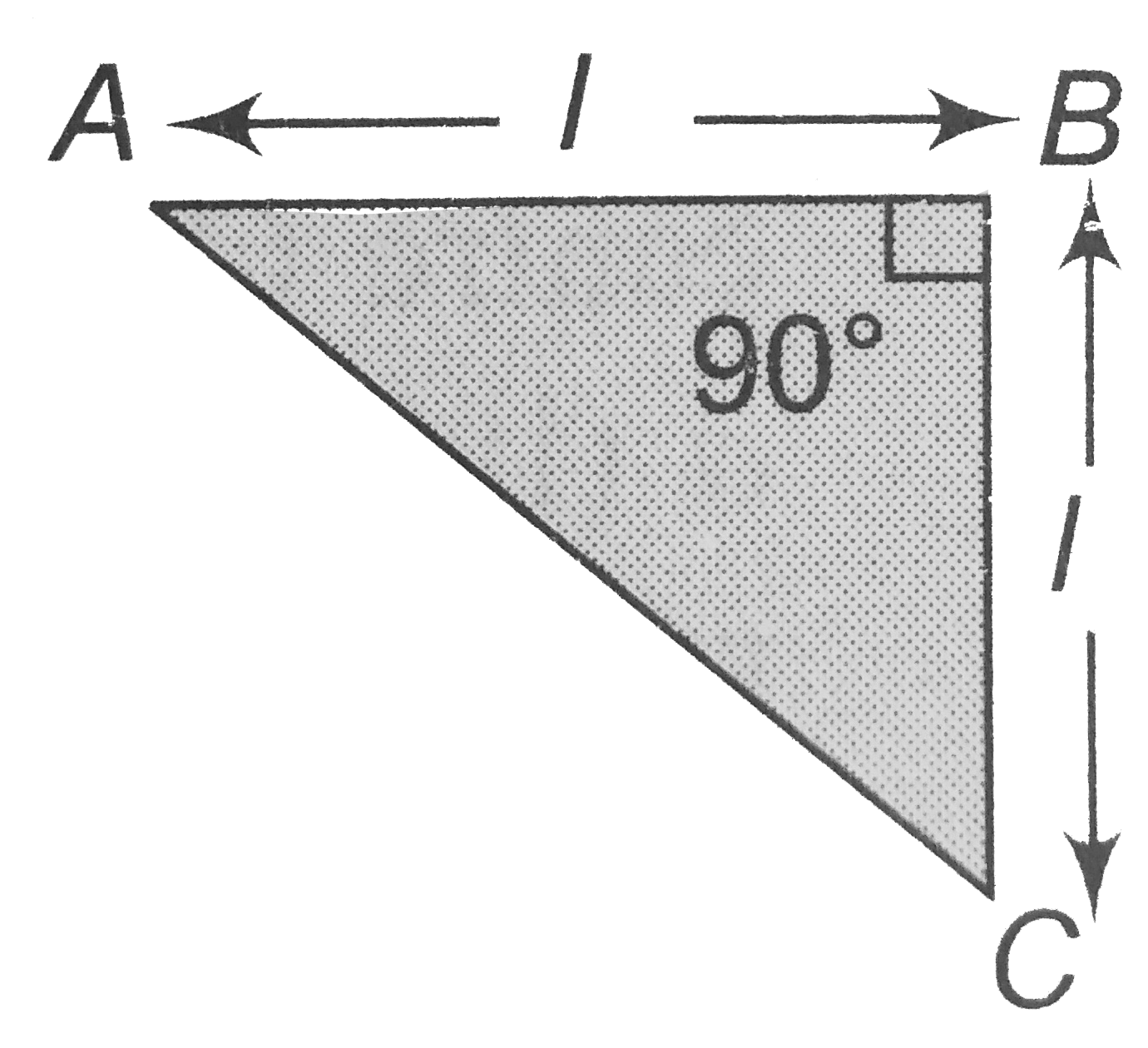 .
.
View SolutionABC is a traiangular plate of uniform thickness. The sides are in the ratio shown in the figure. IAB, IBC and ICA are the moments of inertia of the plate about AB, BC and CA repectively. Which one of the following relations is correct?
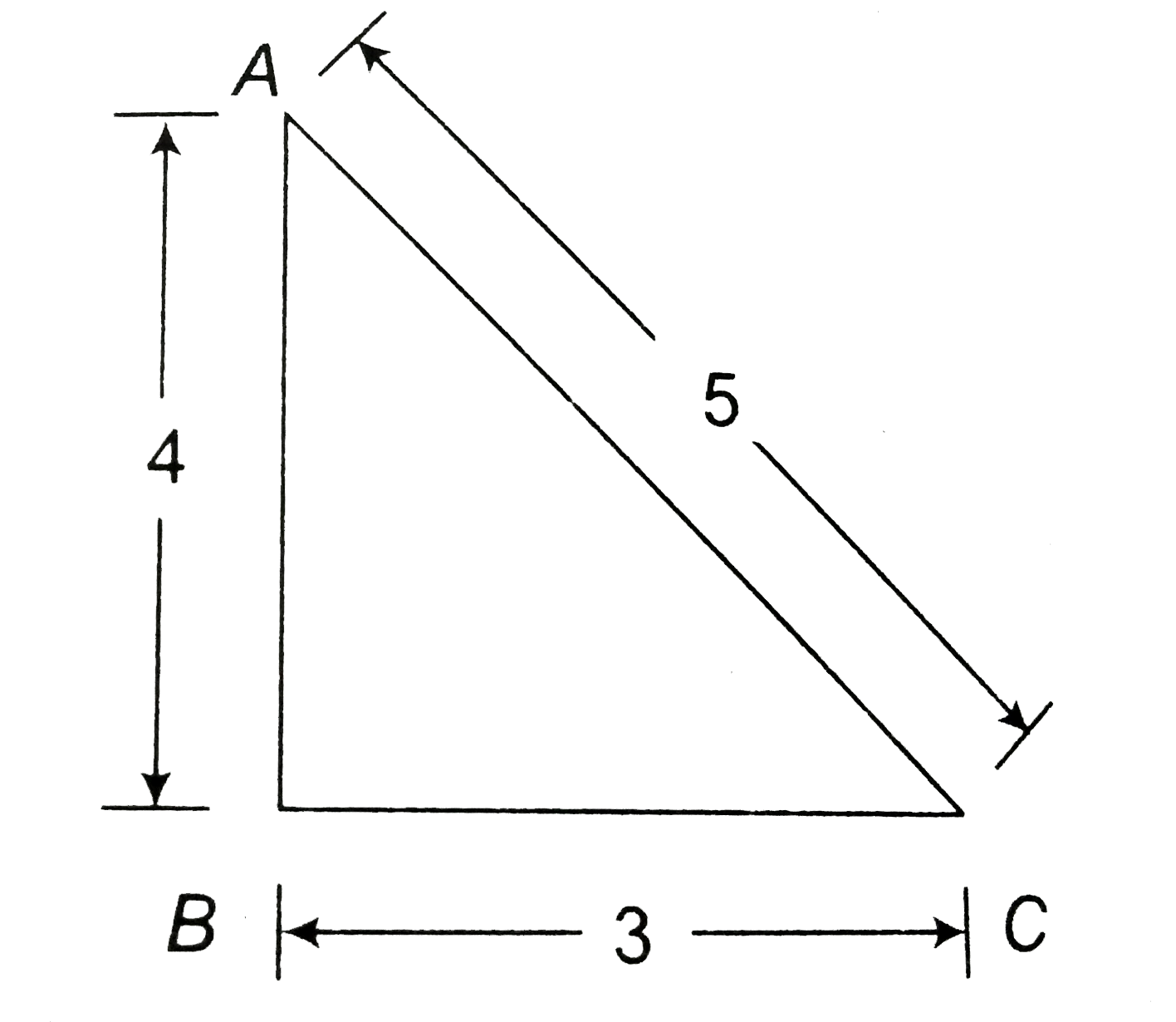
View Solution
