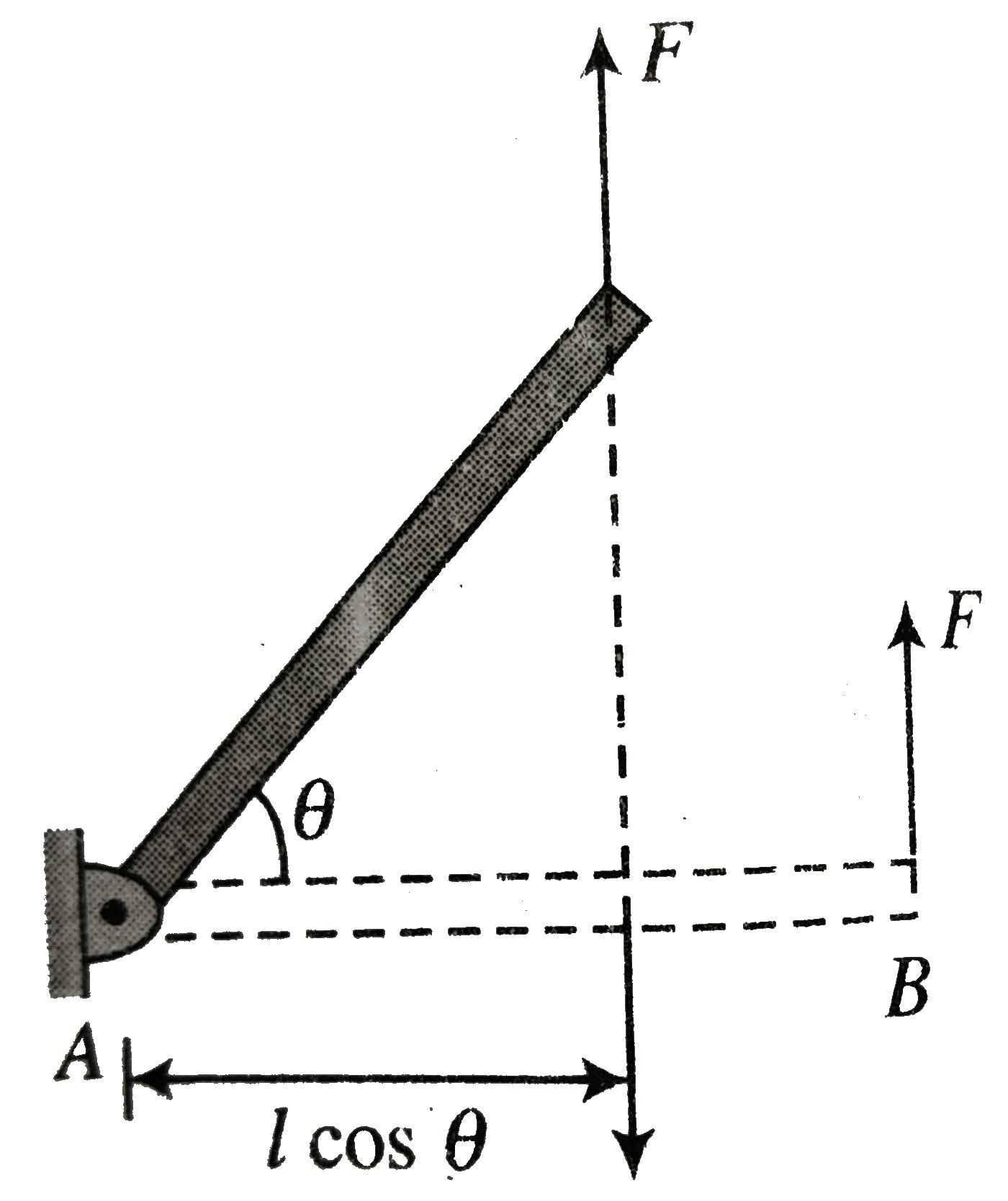
A thin horizontal uniform rod of mass and length can rotate freely about a vertical axis passing through its end . At a certain moment, the end starts experiencing a constant force which is always perpendicular to the original position of the stationary rod and directed in a horizontal plane. The angular velocity of the rod as a function of its rotation angle measured relative to the initial position should be.
Work done by the torque
Now using work energy theorem
Which gives
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Solved Examples
Explore 12 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.1
Explore 11 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICS ENGLISHChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA thin uniform rod of length l and mass m is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is ω. Its centre of mass rises to a maximum height of -
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View SolutionA uniform rod of mass m and length l0 is rotating with a constant angular speed ω about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle θ to the vertical (axis of rotation).
View Solution
A uniform rod of mass m is rotated about an axis passing through point O as shown. Find angular momentum of the rod about rotational law.
View SolutionA thin uniform rod of mass M and length L. Find the radius of gyration for rotation about an axis passing through a point at a distance ofL4 from centre and perpendicular to rod.
View SolutionA thin uniform rod of mass M and length L. Find the radius of gyration for rotation about an axis passing through a point at a distance ofL4 from centre and perpendicular to rod.
View SolutionMoment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
View SolutionA rod of mass m and length L , lying horizontally is free to rotate about a vertical axis through its centre. A horizontal force of constant magnitude F acts on the rod at a distance of L/4 from the centre. The force is always perpendicular to the rod. Find the angle rotated by the rod during the time t after the motion starts.
View SolutionA rigid rod of mass m and lengths l, is being rotated in horizontal plane about a vertical axis, passing through one end A. If TA,TBandTC are the tensions in rod at point A, mid point B and point C of rod repsectively, then

View Solution
