A force F is applied onn a spool (mass m and radius R) in vertical direction as shown in case I and case II. The radius of gyration k of spool is R/(√2). Assuming pure rolling, find the acceleration of the CM of the body, assuming it as a uniform cylinder of mass m.

As the cylinder is rolling. The point of contact will be instantaneus centre of rotation (ICR). The rollig body can be considered as pure rotation about the point of contact.
Case I: The force F provides anticlockwise torque about P. The cylinder will rotate in antclockwise direction about P. The point P is in instantaneous centre of rotation (ICR). The cylinder wil also rotate in anticlock wise direction about its centre of mass. The cylinder will accelerate in left direction. Hence friction will act in left direction.

Applying torque equation about P
F(R2)=IPα=m(k2+R2)α=m(R2k2+R2)α
which gives Rα=F3m
But acceleration of cylinder is α=Rα
Hence a=F3m (towards left).
Case II. In this cae the torque of F about instantaneous centre of rotation (ICR) is in clockwise direction. the cylinder will also rotate in clockwse direction about its centre of mass. Hence, the acceleration of cylinder will e towards right and friction will act towars right.

Now the torque equation about P will be same as we got in previous case. We will get the same value of acceleration but direction be towards right.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples
12 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
If a tangential force mg is applied to a disc of mass m and radius r, the angular acceleration produced in it is?
View SolutionThree rings each of mass m and radius r are so placed that they touch each other. The radius of gyration of the system about the axis as shown in the figure is
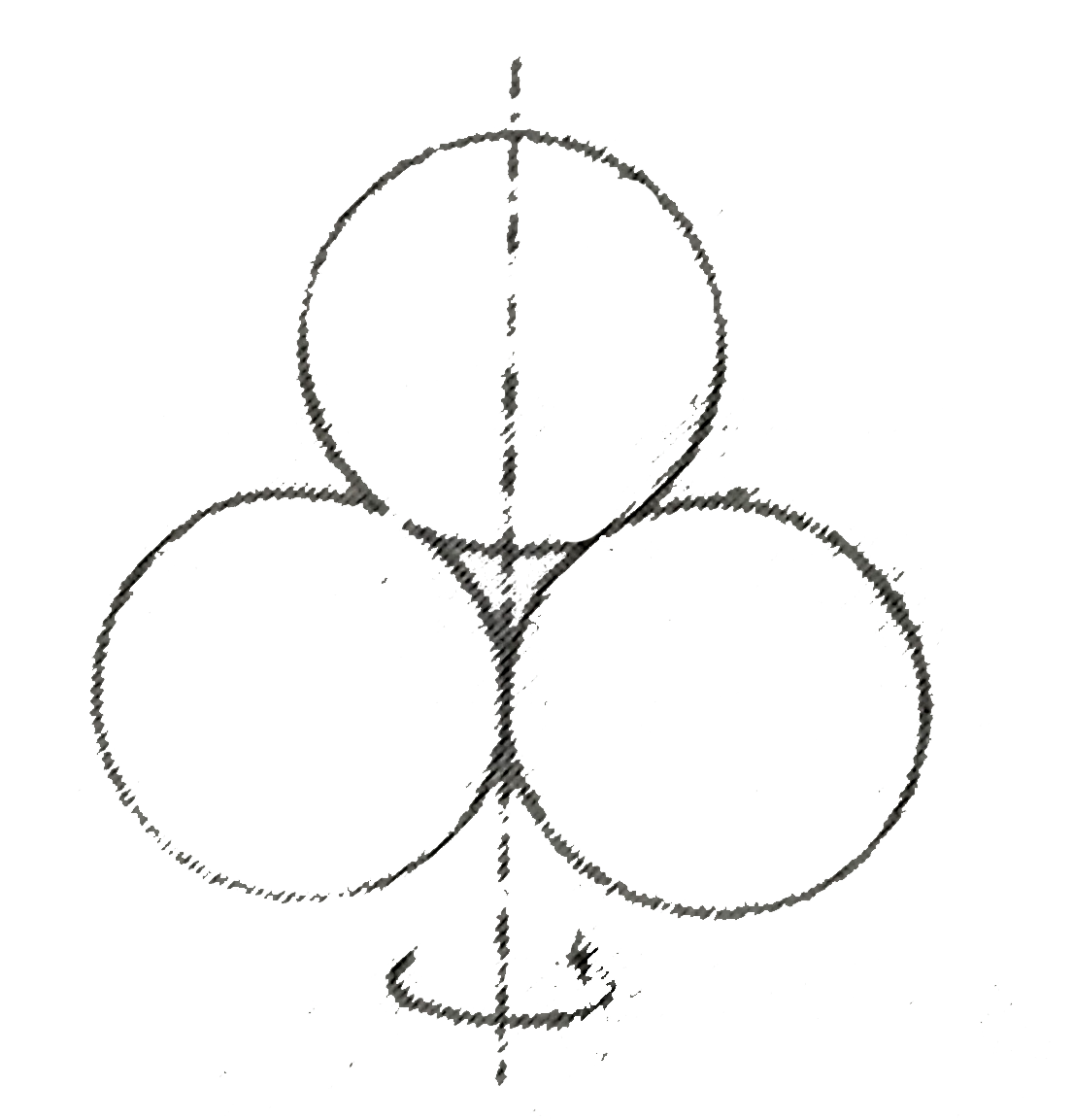
View Solution
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder is
View SolutionA homogeneous cylinder of mass Mand radius r is pulled on a horizontal plane by a horizontal force F acting through its centre of mass. Assuming rolling without slipping, find the angular acceleration of the cylinder,
View SolutionA homogeneous cylinder of mass Mand radius r is pulled on a horizontal plane by a horizontal force F acting through its centre of mass. Assuming rolling without slipping, find the angular acceleration of the cylinder,
View SolutionFind the centre of mass of a uniform semicircular ring of radius R and mass M.
View SolutionA uniform solid sphere of mass m and radius r is suspended symmetrically by a uniform thin spherical shell of radius 2r and mass m.
View SolutionA force of magnitude F is acting on rolling body of mass m and radius R as show in figure. What happens when it enters on a smooth surface?

View SolutionA spool of mass M and radius 2R lies on an inclined plane as shown in the figure. A light thread is wound around the connecting tube of the spool and its free end carries a weight of mass m. The value of m so that system is in equilibrium is
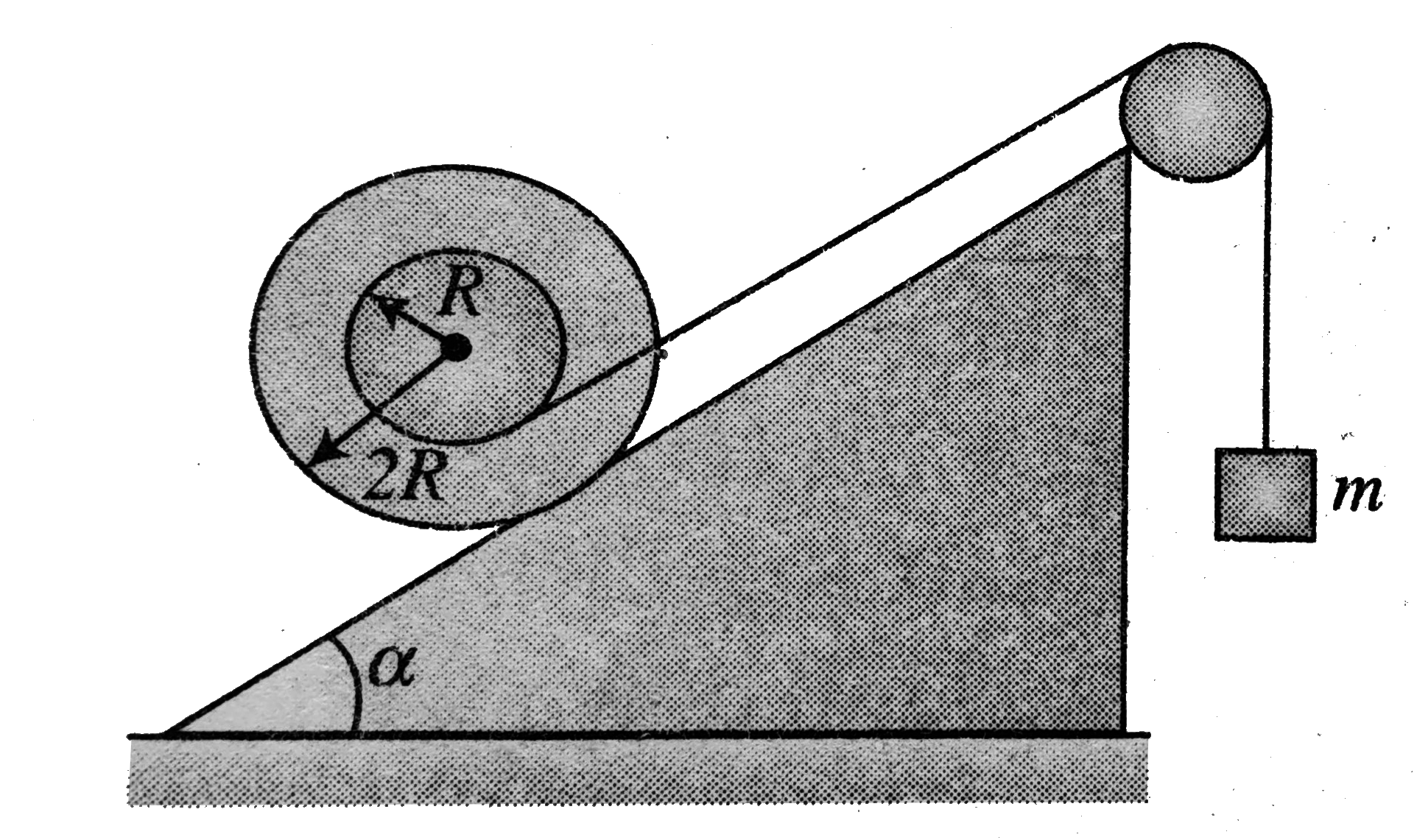
View SolutionA uniform sphere has a mass M and radius R. Find the pressure p inside the sphere, caused by gravitational compression, as a function of the distance r from its centre. Evaluate p at the centre of the Earth, assuming it to be a uniform sphere.
View Solution
