Three identical solid spheres move down three incline A,B and C are all of the same dimensions. A is without friction, the friction between B and a sphere is sufficient to cause rolling without slipping, the friction between C and a sphere causes rolling with slipping. The kinetic energies, of A,B,C at the bottom of the inclines are EA,EB,EC.
EA=EB−EC
EA=EB>EC
EA>EB>EC
EA>EB=EC
The correct Answer is:B
To solve the problem, we need to analyze the motion of three identical solid spheres moving down three different inclined planes (A, B, and C) and determine the kinetic energies EA, EB, and EC at the bottom of the inclines.
1. Understanding the Setup:
- All three inclines (A, B, and C) have the same height h.
- Incline A is frictionless.
- Incline B has sufficient friction to cause rolling without slipping.
- Incline C has friction that causes rolling with slipping.
2. Applying the Work-Energy Theorem:
- The work done by gravity on each sphere as it moves down the incline is equal to the change in kinetic energy.
- The work done by gravity for all three cases is given by:
W=mgh
- Therefore, for each incline:
WA=WB=WC=mgh
3. Analyzing Incline A (Frictionless):
- Since there is no friction, all the gravitational potential energy is converted into kinetic energy.
- Thus, the kinetic energy at the bottom is:
EA=mgh
4. Analyzing Incline B (Rolling without Slipping):
- For rolling without slipping, the sphere has both translational and rotational kinetic energy.
- The total kinetic energy can be expressed as:
EB=12mv2+12Iω2
- For a solid sphere, the moment of inertia I is 25mr2, and the relationship between linear velocity v and angular velocity ω is ω=vr.
- Substituting I and ω into the kinetic energy equation gives:
E_B = \frac{1}{2} mv^2 + \frac{1}{2} \left(\frac{2}{5} m r^2\right \left(\frac{v}{r}\right)^2 = \frac{1}{2} mv^2 + \frac{1}{5} mv^2 = \frac{7}{10} mv^2
- Since the work done by gravity is equal to the kinetic energy:
mgh=710mv2⇒EB=mgh
5. Analyzing Incline C (Rolling with Slipping):
- In this case, the sphere slips down the incline, and some energy is lost due to friction.
- The work done by friction is negative, which means:
WC+Wfriction=ΔKE
- Here, the work done by friction reduces the total kinetic energy:
mgh+Wfriction=EC
- Since Wfriction<0, we can conclude that:
EC<mgh
6. Final Comparison:
- From the analysis, we have:
EA=mgh,EB=mgh,EC<mgh
Conclusion:
- The kinetic energies at the bottom of the inclines are:
- EA=EB>EC
- All three inclines (A, B, and C) have the same height h.
- Incline A is frictionless.
- Incline B has sufficient friction to cause rolling without slipping.
- Incline C has friction that causes rolling with slipping.
- The work done by gravity on each sphere as it moves down the incline is equal to the change in kinetic energy.
- The work done by gravity for all three cases is given by:
W=mgh
- Therefore, for each incline:
WA=WB=WC=mgh
- Since there is no friction, all the gravitational potential energy is converted into kinetic energy.
- Thus, the kinetic energy at the bottom is:
EA=mgh
- For rolling without slipping, the sphere has both translational and rotational kinetic energy.
- The total kinetic energy can be expressed as:
EB=12mv2+12Iω2
- For a solid sphere, the moment of inertia I is 25mr2, and the relationship between linear velocity v and angular velocity ω is ω=vr.
- Substituting I and ω into the kinetic energy equation gives:
E_B = \frac{1}{2} mv^2 + \frac{1}{2} \left(\frac{2}{5} m r^2\right \left(\frac{v}{r}\right)^2 = \frac{1}{2} mv^2 + \frac{1}{5} mv^2 = \frac{7}{10} mv^2
- Since the work done by gravity is equal to the kinetic energy:
mgh=710mv2⇒EB=mgh
- In this case, the sphere slips down the incline, and some energy is lost due to friction.
- The work done by friction is negative, which means:
WC+Wfriction=ΔKE
- Here, the work done by friction reduces the total kinetic energy:
mgh+Wfriction=EC
- Since Wfriction<0, we can conclude that:
EC<mgh
- From the analysis, we have:
EA=mgh,EB=mgh,EC<mgh
- The kinetic energies at the bottom of the inclines are:
- EA=EB>EC
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping. Force of friction between sphere and plank is

View SolutionA hollow sphere rolls down a rough inclined plane whose angle of inclination is θ, with horizontal. For the hollow sphere to undergo pure rolling, without slipping, the condition is [μ = coefficient of friction between the hollow sphere and inclined plane]
View SolutionWhat is the minimum coefficient of friction for a solid sphere to roll without slipping on an inclined plane of inclination θ ?
View SolutionA rolling body is kept on a plank B. There is sufficient friction between A and B and no friction between B and the inclined plane. Then body:
View SolutionA solid sphere is rolling without slipping on a horizontal plane. The ratio of its rotational kinetic energy and translational kinetic energy is
View SolutionA disc and a solid sphere of same mass and radius roll down an inclined plane. The ratio of thhe friction force acting on the disc and sphere is
View SolutionA solid sphere rolls on horizontal surface without slipping. What is the ratio of its rotational to translation kinetic energy.
View SolutionA block A of mass M rests on a wedge B of mass 2M and inclination θ. There is sufficient friction between A and B so that A does not slip on B. If there is no friction between B and ground, the compression in spring is
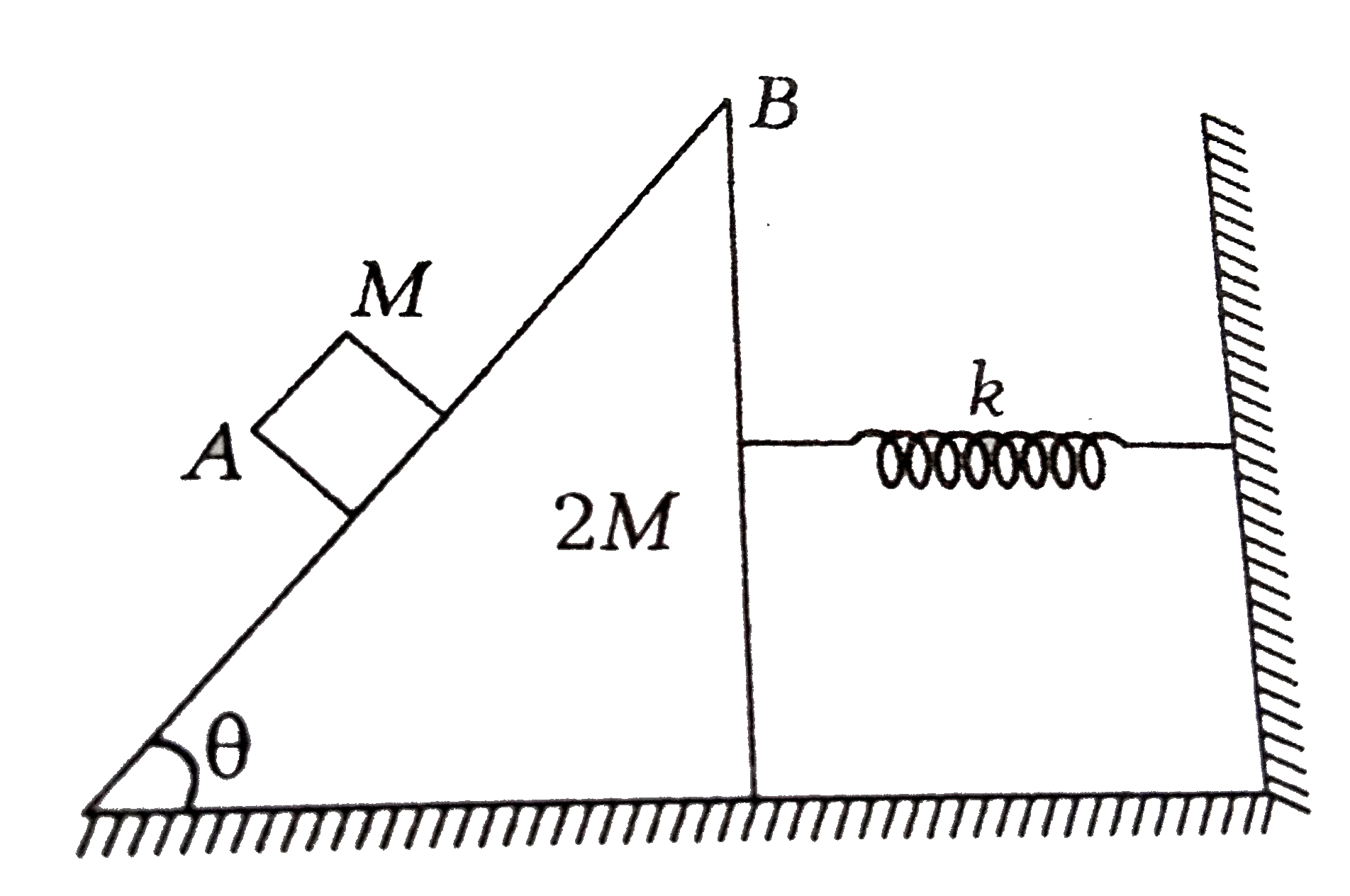
View SolutionA block A of mass M rests on a wedge B of mass 2M and inclination θ. There is sufficient friction between A and B so that A does not slip on B. If there is no friction between B and ground, the compression in spring is

View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.When a horizontal force F is applied at centre of sphere, acceleration of the plank is

View Solution
